عندما أتعمق في موضوع التنبؤ انحناء نصف القطر الداخلي عند استخدام مكبس الثني، وجدتُ أن فهم تعقيدات هذه العملية يُؤثر بشكل كبير على جودة مشاريع تصنيع المعادن لدينا. يلعب نصف القطر الداخلي دورًا حاسمًا في ضمان دقة الانحناءات وتحقيق النتائج المرجوة. في هذه المقالة، سأشارككم رؤىً وتقنياتٍ ساعدتني على التنبؤ بنصف القطر الداخلي بفعالية عند استخدام مكبس الثني، مما يُعزز الكفاءة والدقة في عملياتنا. انضموا إليّ لنستكشف هذا الجانب الأساسي من أعمال المعادن!

إن التنبؤ بنصف القطر لا يكون دقيقًا بنسبة 100 بالمائة، ولكن هذا هو أفضل ما يمكن الحصول عليه.

يمكنك استخدام بعض القواعد العامة للتنبؤ بانحناء نصف قطر الانحناء الداخلي عند تكوين الهواء، وعادةً ما تكون النتائج التي تحصل عليها قريبة بدرجة كافية، ولكن بمساعدة عدد قليل من الآلات الحاسبة عبر الإنترنت، يمكنك الحصول على نتائج أقرب.

إذا كنت تتابع مناقشتنا في الأشهر الأخيرة نصف قطر الانحناء ومن أين يأتي، أهلاً بعودتك. على أي حال، لنرَ إلى أي عمقٍ سيصل هذا النفق الدائري.

في مقالات سابقة، ناقشتُ قواعد عامة مختلفة يستخدمها المشغّلون في الورشة لإنجاز العمل. هذه القواعد قد تُساعدك على توقع نصف قطر الانحناء الداخلي بدقة، بل ويمكنك أيضًا التقدّم أكثر.

ما هو الفرق الذي يحدثه ذلك؟

خذ في الاعتبار موقفًا نموذجيًا حيث تستخدم قاعدة 20 بالمائة، والتي تنص على أن نصف قطر الانحناء الهوائي يتشكل كنسبة مئوية من فتحة القالب، من 20 إلى 22 بالمائة للفولاذ المقاوم للصدأ وحوالي 16 بالمائة للفولاذ المدلفن على البارد 60-KSI، مادة الأساس لدينا.

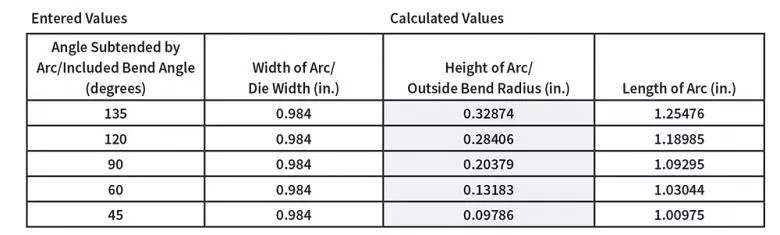
لنفترض أنك تُثني ألومنيومًا ناعمًا بمقاومة 13-KSI بعرض قالب 0.984 بوصة ونصف قطر ثقب 0.032 بوصة. كنقطة بداية، تحسب نصف قطر الانحناء الداخلي عند 16% من فتحة القالب ليكون 0.157 بوصة، مع أن هذا ينطبق على مادة بمقاومة 60-KSI، لذا ستحتاج إلى التكيف مع نوع المادة. في هذه الأثناء، عند الحساب لمعرفة ما إذا كان الانحناء سيصبح حادًا، تجد أن الحد الأدنى لنصف القطر قبل أن يبدأ الثقب بتجعد خط الانحناء هو 0.172 بوصة. أخيرًا، تُجري اختبار انحناء، لتجد أن نصف القطر الفعلي هو 0.170 بوصة.

لديك نصف قطر ٠٫١٥٧ بوصة محسوبًا وفقًا لقاعدة ٢٠٪، ثم لديك نصف قطر ٠٫١٧٢ بوصة محسوبًا وفقًا لحسابات الانحناء الحاد. هذا فرق في نصف القطر قدره ٠٫٠١٥ بوصة. أليس هذا كافيًا؟ في هذه الحالة، عند تطبيق الفرق على خصم الانحناء، يمكن أن يصل إلى ٠٫٠٠٩ بوصة لكل انحناءة.

هل سبق لك أن صنعت قطعة بأربع حواف جانبية مع أربع حواف إضافية على طول الجزء العلوي، لتجد أن إحدى الزوايا مثالية، واثنتين منها مرضيتين بشكل طفيف، وثالثة سيئة المظهر؟ لماذا يحدث هذا؟ خطأ بسيط في حساب الانحناء ناتج عن اختلافات في حسابات نصف قطر الانحناء الداخلي يُحدث فرقًا كبيرًا إذا كنت ترغب في الحصول على قطع مثالية من المرة الأولى.

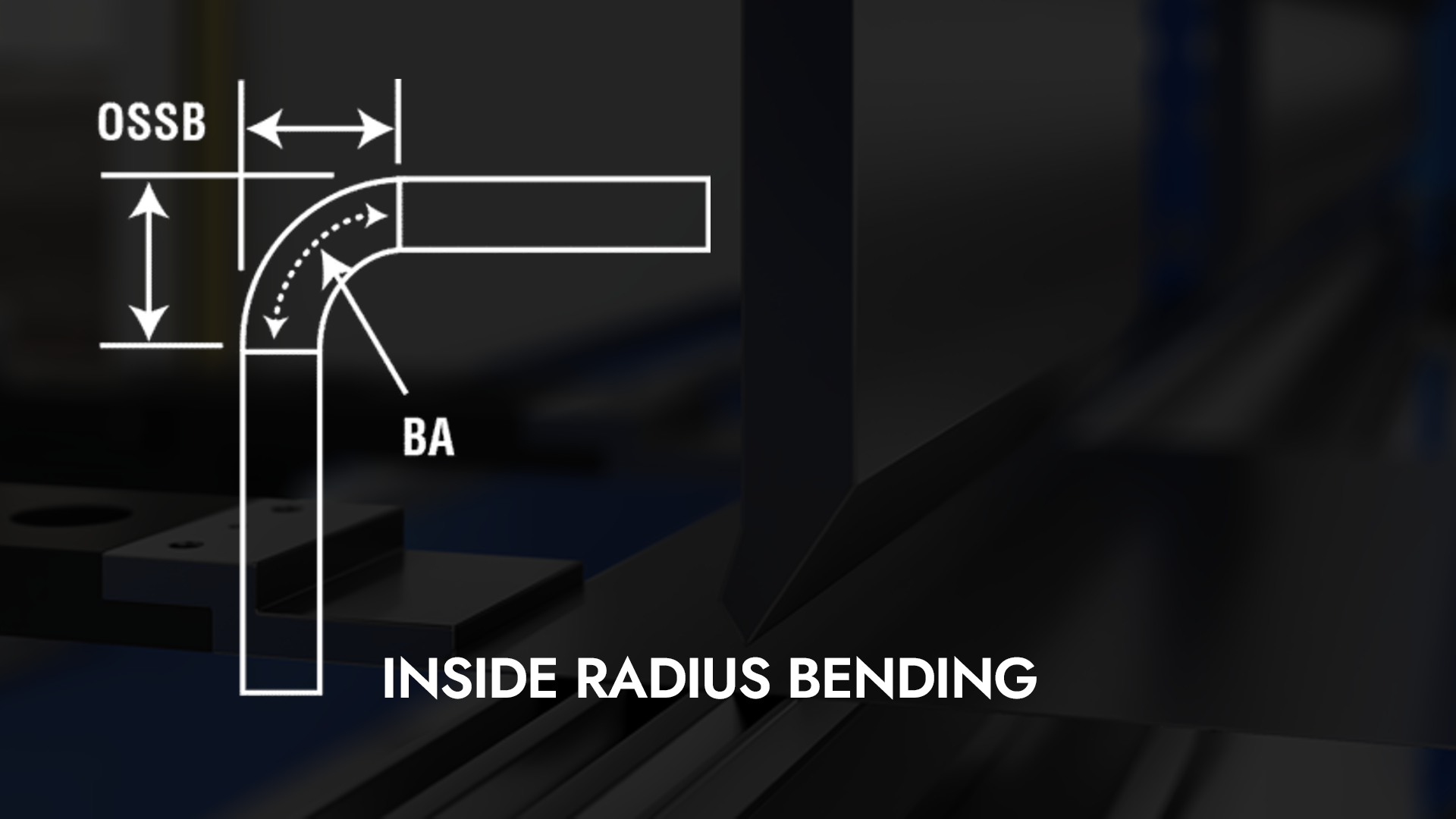
جوهر أي عملية ثني هو نصف القطر الداخلي للانحناء. إذا أمكن حساب استنتاج الانحناء بناءً على النتائج الفعلية، فستكون الدقة مضمونة. العيب الوحيد في هذه النظرية هو أننا في كثير من الأحيان لا نشكل نصف قطر حقيقي أثناء التشكيل. قد يكون الشكل الذي نشكله قطعًا مكافئًا، وهو منحنى معكوس متماثل، وعادةً ما يكون على شكل حرف U عند توجيهه كما هو موضح في الشكل 1. ونصف القطر النهائي الذي نحصل عليه هو نتيجة الارتداد.

• تأثيرات الزنبرك

إذن، كيف يمكننا التنبؤ بدقة انحناء نصف القطر الداخلي واستنتاج الانحناء الصحيح؟ لتحقيق ذلك يدويًا، تتعمق الرياضيات في التفاصيل، لذا لن أخوض في هذا الموضوع. بدلاً من ذلك، سنستخدم ببساطة آلتين حاسبتين مختلفتين على الإنترنت.

الأول موجود على www.harsle.com. انقر على "حاسبة القوس الدائرية الكاملة". لاحظ أن قيمة عرض القوس في الحاسبة تساوي عرض القالب، وأن الزاوية التي يغطيها القوس تساوي زاوية الانحناء المضمنة.

تأكد من أن إعدادات أبعاد الآلة الحاسبة صحيحة للبيانات التي تستخدمها - البوصات، الأقدام، المليمترات، وما إلى ذلك. لاحظ أنه عندما نضغط على Enter، فإن الإجابات التي نحصل عليها هي رياضية بحتة ولم يتم أخذها في الاعتبار لقوة الشد المادية.

المعلومات التي نبحث عنها في الآلة الحاسبة هي ارتفاع القوس، الذي يُعادل نصف قطر الانحناء الخارجي. لنحسب قيمة خط الأساس، وهو فولاذ مدرفل على البارد بقياس 60-KSI، بسمك 0.125 بوصة، باستخدام عرض قالب 0.984 بوصة. يُرجى العلم أننا نتحدث عن التشكيل الهوائي، لذا لن تُحدث زاوية القالب فرقًا؛ يمكن أن يكون قالبًا على شكل قناة، أو حادًا، أو على شكل حرف V. العرض هو المهم.

أولاً، دعنا ندخل إلى الزاوية المريحة - تلك الزاوية 90 درجة التي نريد تحقيقها.

القيم المدخلة

الزاوية الموجهة بواسطة القوس (بما في ذلك زاوية الانحناء): 90 درجة

عرض القوس (عرض القالب): 0.984 بوصة.

القيمة المحسوبة

ارتفاع القوس (نصف قطر الانحناء الخارجي): 0.20379 بوصة.

مع ذلك، لا تأخذ هذه الحسابات في الاعتبار الارتداد. في مثالنا، سنستخدم قيمة 1 درجة للارتداد، والتي تحدث عندما تكون لدينا علاقة تقريبية 1:1 بين سمك المادة ونصف قطر الانحناء الداخلي. بعد تخفيف ضغط التشكيل، ترتدّ المادة بمقدار 1 درجة، وللتعويض، نستخدم الآن زاوية انحناء 89 درجة. باستخدام حاسبة القوس الدائري الكاملة على موقع harsle.com، نُدخل ما يلي:

القيم المدخلة

عرض القوس (عرض القالب): 0.984 بوصة.

الزاوية التي يغطيها القوس (بما في ذلك زاوية الانحناء): 89 درجة

القيمة المحسوبة

ارتفاع القوس (نصف قطر الانحناء الخارجي): 0.201 بوصة.

  الآن نأخذ قيمة ارتفاع القوس لزاوية الانحناء الجديدة وندخلها في الصيغة التالية:

ارتفاع القوس – (2 × سمك المادة 2) = نصف القطر الداخلي

0.201 – (2 × 0.01562) = نصف قطر الانحناء الداخلي

0.201 – 0.031 = 0.170 بوصة نصف قطر الانحناء الداخلي

  لاحظ أن طريقة حساب ارتفاع القوس هذه تختلف عن الطريقة التي اتبعناها في عمود "أساسيات الانحناء" الشهر الماضي، عندما استخدمنا طول القوس. في الشهر الماضي، حسبنا نصف القطر الداخلي بناءً على عرض فتحة القالب؛ وهذه المرة نستخدم نصف قطر محدد.

  في الشهر الماضي، حسبنا نصف قطر قدره 0.136 بوصة، والآن حسبنا نصف القطر الداخلي بطريقة مختلفة، وحصلنا على 0.170 بوصة، بفارق 0.034 بوصة. علاوة على ذلك، إذا استخدمنا قاعدة الـ 20% (مرة أخرى، بالنسبة للفولاذ المدرفل على البارد 60-KSI، يُحسب نصف القطر ليكون حوالي 16% من عرض القالب)، فسنحسب نصف قطر داخلي قدره 0.157 بوصة، أي في منتصف المسافة بين القياسين السابقين. هذه كلها طرق مختلفة لحساب نصف القطر، بنتائج مختلفة قليلاً. ولكن، نعم، الأمر يزداد تعقيدًا!

• القطع المكافئ والانحناءات الحادة

إذا كنت تستخدم قيمة نصف قطر الثقب تساوي أو تقل عن الحد الأدنى لنصف قطر الانحناء الحاد لتشكيل الهواء لجزء، فلن تقوم بعد الآن بإنشاء نصف قطر في الجزء (لمزيد من المعلومات حول الانحناءات الحادة، بدلاً من ذلك، ستقوم بإنشاء قطع مكافئ. أنت في الواقع تسحب طول قوس مختلفًا إلى فتحة القالب.

وللتنبؤ بكيفية تشكل هذا القطع المكافئ، يمكننا اللجوء إلى حاسبة أخرى عبر الإنترنت:

نُدخل نصف القطر الخارجي وعرض القالب لإيجاد طول قوس القطع المكافئ. قيمة الارتفاع في هذه الحاسبة الإلكترونية تعادل نصف قطر الانحناء الخارجي، بينما قيمة العرض تعادل عرض القالب.

القيم المدخلة

الارتفاع: (نصف القطر الخارجي): 0.201 بوصة.

العرض (عرض القالب): 0.984 بوصة

القيمة المحسوبة

طول القوس: 1.0845 بوصة

هنا، عمق القطع المكافئ (أو ارتفاع القوس) هو 0.201 بوصة، وطول قوس القطع المكافئ هو 1.0845 بوصة. تذكر هذه القيم. بالعودة الآن إلى حاسبة القوس الدائرية الكاملة على الموقع www.harsle.com، نُدخل طول القوس عند 1.0845 بوصة وعرض القالب عند 0.984 بوصة.

القيم المدخلة

طول القوس: 1.0845 بوصة

عرض القوس (عرض القالب): 0.984 بوصة.

القيم المحسوبة

ارتفاع القوس (نصف قطر الانحناء الخارجي): 0.195 بوصة.

الزاوية التي يحيط بها القوس

(زاوية الانحناء المضمنة): 86.679 درجة

عند القيام بذلك، ستجد أن ارتفاع القوس (أي نصف القطر الخارجي) هو 0.195 بوصة، وهو أصغر قليلاً من نصف القطر الخارجي البالغ 0.201 بوصة من الآلة الحاسبة السابقة، والتي لم تأخذ في الاعتبار تأثير القطع المكافئ. بمعرفة ذلك، يمكننا القول بثقة أن نصف القطر الداخلي يتناقص عند تكوين قطع مكافئ، وهو ما يحدث عند استخدام نصف قطر ثقب أقل من الحد الأدنى لنصف قطر الانحناء الحاد. لاحظ أن القطع المكافئ يتطلب أيضًا زاوية انحناء أكبر لإنتاج زاوية الانحناء المريحة المطلوبة؛ فقد انتقلنا من زاوية انحناء متضمنة 89 درجة إلى 86.68 درجة، مع 2.32 درجة إضافية من الارتداد. لاحظ أيضًا أن نصف القطر الداخلي للقطعة لن يصبح أصغر من نصف قطر أنف الثقب.

• زاوية ونصف قطر الانحناء

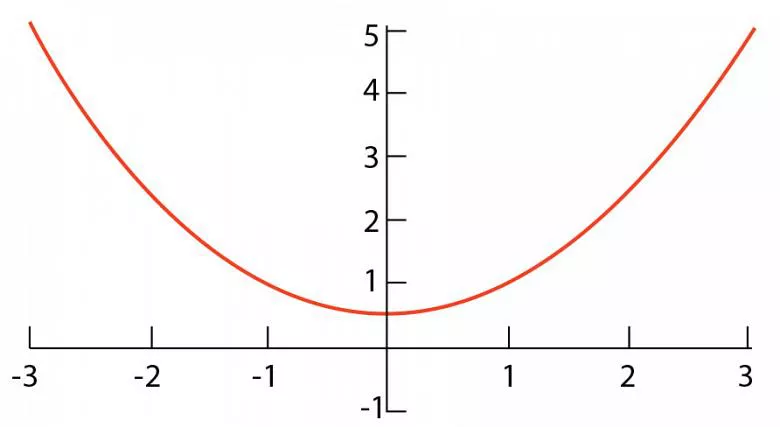
تذكر أن أي تغيير في نصف القطر يؤدي إلى تغيير في زاوية الانحناء. إذا أدخلنا عرض القالب وزاوية الانحناء المضمنة على موقع www.harsle.com، فسنحصل على النتائج الموضحة في الشكل 2.

تظهر النتائج أنه عندما تقوم بتشكيل الهواء، فإن نصف القطر يتناقص مع زاوية الانحناء المضمنة (باستثناء الانحناءات الحادة).

تتوقف علاقة زاوية الانحناء/نصف القطر هذه عند زوايا متضمنة أقل من 28 درجة متضمنة (152 درجة تكميلية)، على الرغم من أن الحد الأدنى للزاوية المتضمنة قد يكون أكبر في المواد ذات الارتداد الكبير.

هذا صحيح جزئيًا لأن الحد الأدنى لزاوية ثقب مكبس الثني هو ٢٨ درجة. مع ذلك، فإن الاستمرار في إغلاق الانحناء بما يتجاوز ٢٨ درجة سيؤدي إلى نوع من التسطيح. سيتم سحق نصف القطر حتى يتم الوصول إلى زاوية الانحناء المطلوبة أو اكتمال عملية الحاشية. (ملاحظة جانبية سريعة: بالنسبة للحاشية المغلقة، يكون نصف القطر صفرًا، ويُحسب خصم الانحناء كنسبة مئوية من سمك المادة - ٤٣٪ في الظروف المثالية، مع أن هذه العملية تعتمد بشكل كبير على المشغل).

• العوامل المؤثرة في قوة الشد

في المثال السابق، استخدمنا درجة واحدة من الارتداد لإجراء الحسابات. بالنسبة للفولاذ المدرفل على البارد الخفيف 60-KSI، يبلغ متوسط الارتداد درجة واحدة أو أقل. ماذا عن المواد الأخرى؟

لهذا، يُمكننا التنبؤ بالارتداد بدقة معقولة باستخدام الصيغة التالية، والتي تتطلب منا تحويل جميع القيم إلى وحدات مترية. يُرجى ملاحظة أن التنبؤ بالارتداد ليس دقيقًا تمامًا. مع ذلك، تُؤدي هذه الصيغ وظيفة جيدة جدًا.

[(نصف القطر الداخلي بالمليمترات/2)/

سمك المادة بالمليمترات] × عامل الشد

عامل الشد = قوة الشد المادية بالرطل لكل بوصة مربعة/60,000

أولاً، دعنا نحسب الارتداد كما لو كنا نعمل مع مادة أساسية 60-KSI بنصف قطر انحناء داخلي يبلغ 0.170 بوصة:

[(نصف القطر الداخلي بالمليمترات/2)/

سمك المادة بالمليمترات] × عامل الشد

سمك المادة: 0.125 بوصة × 25.4 = 3.175 مم

نصف قطر الانحناء الداخلي: 0.170 بوصة × 25.4 = 4.318 مم

(4.318/2) /3.175

2.159 مم / 3.175 مم = 0.68 درجة من الارتداد

في هذا المثال، سنُقرّب هذا إلى درجة واحدة. ثم يُمكننا تطبيق مُعامل الشد على الفولاذ المقاوم للصدأ 88-KSI 304.

عامل الشد = قوة الشد المادية بالرطل لكل بوصة مربعة/60,000

88,000/60,000 = 1.466666

1.0 درجة × 1.466666

هذا يعطينا 1.46 درجة لفولاذ 88-KSI 304 المقاوم للصدأ. وبالتقريب، نحصل على 1.5 درجة من الارتداد المُقدّر بنسبة 1 إلى 1 بين نصف القطر الداخلي وسمك المادة.

• العودة إلى الآلة الحاسبة

الآن، بما أنك تستطيع تقدير زاوية الارتداد بدقة معقولة، يمكنك الآن تعويضها. لتحديد الزاوية التي تحتاجها لتعويض زاوية الارتداد، ما عليك سوى طرح قيمة زاوية الارتداد إذا كنت تستخدم زوايا انحناء متضمنة، أو جمعها إذا كنت تستخدم زوايا انحناء متكاملة. تعمل حاسبة القوس الدائري على موقع www.harsle.com مع زوايا الانحناء المتضمنة (المُسماة أيضًا "زاوية القوس المُحيطة").

بمجرد أن تعرف نصف القطر الداخلي - أي نصف القطر الداخلي الفعلي الذي سيظهر في القطعة النهائية - يمكنك بعد ذلك إدراج قيمة نصف القطر هذه في صيغ الانحناء الخاصة بك (انظر الشريط الجانبي).

خاتمة

بالتنبؤ الصحيح بنصف القطر الداخلي، يُمكننا حساب استنتاجات الانحناء بدقة. من بين الطرق العديدة المختلفة التي يُمكن من خلالها التنبؤ بنصف القطر الداخلي، لا توجد طريقة مثالية، ولكن هذه الطريقة تُعتبر الأفضل على الإطلاق. مع ذلك، فإن الانحناء يحتوي على متغيرات كثيرة جدًا لتحقيق دقة 100%.

من الضروري أيضًا في عملية تشكيل الهواء أن يُطلع المهندس أو المبرمج الفني على مجموعات الأدوات التي صُممت باستخدامها أي قطعة منحنية. علاوة على ذلك، يجب على الفني إدراك الأهمية القصوى لاستخدام هذه الأدوات للحصول على قطع عالية الجودة.

في الشهر القادم، سنتناول كيفية حساب نصف القطر الداخلي للانحناءات حيث تكون العلاقة بين نصف القطر الداخلي وسمك المادة كبيرة جدًا - انحناء نصف القطر العميق. الانحناءات ذات نصف القطر الكبير تعاني من مشاكل في زاوية القالب، وعرضه، وتعدد الكسر، وبالطبع، كميات كبيرة جدًا من الارتداد.

لا يزال هناك طريق طويل للوصول إلى جحر الأرنب، لكن الأمر يستحق الرحلة.

مراجعة صيغ الانحناء

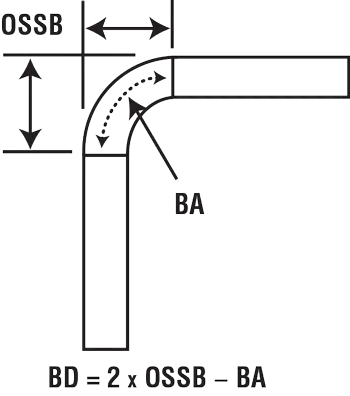
هذه الصيغ لبدل الانحناء، والتراجع الخارجي، وخصم الانحناء راسخة جيدًا، ويمكن استخدام كل قيمة بطرق مختلفة لحساب تخطيط القطعة المسطحة.

الصيغ

BA = [(0.017453 × روبية) + (0.0078 × طن متري)]

× درجات الانحناء التكميلية

OSSB = [ظل (درجة زاوية الانحناء / 2)]

× (Mt + Rp)

BD = (OSSB × 2) – BA

مفتاح

Rp = نصف قطر أنف اللكمة (القاع)

أو نصف القطر العائم الداخلي (تشكيل الهواء)

Mt = سمك المادة

BA = بدل الانحناء

BD = خصم الانحناء

OSSB = التراجع الخارجي

0.017453 = π/180

0.0078 = عامل K × π / 180

عامل K = 0.446