Al trabajar en proyectos, es crucial comprender la importancia de determinar la longitud real de un componente. Unas mediciones precisas garantizan que los componentes encajen perfectamente y funcionen correctamente. En este artículo, compartiré métodos y consejos prácticos que he encontrado eficaces para determinar la longitud real de diversos componentes. Tanto si trabajas en proyectos de fabricación como de bricolaje, dominar esta habilidad puede mejorar considerablemente tu precisión y eficiencia. ¡Analicemos las mejores prácticas para lograr mediciones precisas!

En el procesamiento de chapa de metal A menudo se encuentran piezas de diversas formas, como tuberías de ventilación, juntas deformadas, etc. Para completar su procesamiento, primero se debe desdoblar la chapa metálica, extendiendo la superficie del objeto sobre un plano según su forma y tamaño reales. El desdoblado de la chapa metálica es un proceso preparatorio para... chapa de metal El material es fundamental para el correcto procesamiento de las piezas de chapa metálica. Para dibujar correctamente un diagrama de desplegado de chapa metálica, es necesario conocer las dimensiones reales del diagrama o las dimensiones reales de sus componentes. Si la superficie tridimensional de la línea y la superficie de proyección no son paralelas, la longitud real de la proyección no se refleja en los dibujos de diseño. Por lo tanto, antes del desplegado, se debe utilizar un método gráfico para determinar la longitud real del segmento de línea.

Los métodos para determinar la longitud real de un segmento de recta incluyen el método de rotación, el método del triángulo rectángulo, el método del trapezoide rectángulo y el método del plano de proyección auxiliar. El dominio y la aplicación de estos métodos para determinar la longitud real de un segmento de recta son un prerrequisito y la base para la adquisición de habilidades de desplegado de chapa metálica.

El método de rotación

El método de rotación consiste en rotar una línea inclinada alrededor de un eje perpendicular a un plano de proyección hasta una posición paralela a otro plano de proyección, donde el segmento proyectado en dicho plano es la longitud real de la línea inclinada. Para mayor comodidad gráfica, el eje generalmente pasa por uno de los extremos de la línea inclinada; este extremo es el centro del círculo y la línea inclinada es el radio de rotación.

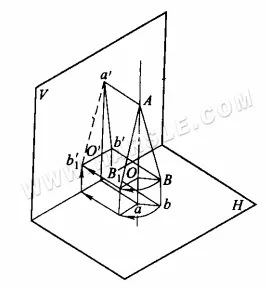
Principio de rotación para longitud real: el diagrama a continuación muestra dicho principio. ab es una línea de posición general, inclinada respecto a cualquier plano de proyección. Tanto la proyección a'b' de ab sobre el plano V como la proyección de ab sobre el plano H son más cortas que la longitud real. Suponiendo que el eje AO es perpendicular al plano H en un extremo de AB, al rotar AB alrededor del eje AO hasta una posición AB1 paralela al plano V, su proyección a'b1' sobre el plano V (la línea discontinua en el diagrama indica la longitud real) reflejará su longitud real.

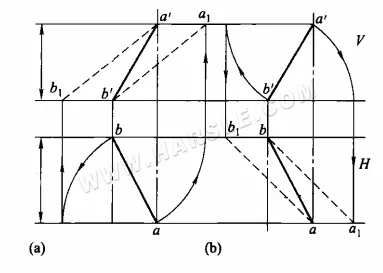
Método de rotación para longitudes reales: El diagrama a continuación muestra el método específico para usar el método de rotación para longitudes reales. En el diagrama (a), la proyección horizontal ab se gira paralela a la proyección ortográfica, lo que resulta en los puntos a1 y b1, que conectan a1b' o a'b1, que es la longitud real del segmento AB. En el diagrama (b), la proyección ortográfica a'b' se gira paralela a la proyección horizontal, lo que resulta en los puntos a1 y b1, que conectan a1b o ab1, que es la longitud real del segmento AB.

Ejemplo: El diagrama a continuación muestra la longitud real de un prisma oblicuo mediante el método de rotación. Como se puede observar en la proyección, la base del prisma oblicuo es paralela al plano horizontal y su proyección horizontal refleja su forma sólida y su longitud real. Las cuatro caras restantes (lados) son dos conjuntos de triángulos, cuyas proyecciones no reflejan la forma real. Para obtener la forma real de los dos conjuntos de triángulos, se debe determinar la longitud real de sus prismas. Dado que la forma es simétrica de adelante hacia atrás, solo se requieren las longitudes reales de los dos prismas laterales para dibujar el diagrama.

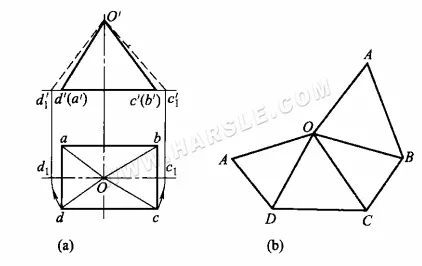
Los pasos específicos para hacer un diagrama de desarrollo son:

1. Utilice el método de rotación para hallar las longitudes reales de las costillas laterales Oc y Od. Como se muestra en el diagrama a continuación, tome O como centro del círculo, Oc y Od como radios de rotación, respectivamente. La línea horizontal en c1, d1 se cruza con la vertical. La proyección ortográfica c'd', que interseca c1'd1', conecta O'c1', O'd1', es la longitud real del prisma lateral Oc y Od.

2. Traza una línea AD de longitud igual a ad en la posición correspondiente del diagrama y dibuja △AOD con A y D como centro del círculo y Od' como radio del arco, intersecando en O; luego, dibuja un arco con O como centro del círculo y Oc1′ como radio, intersecando con el arco formado con D como centro y dc como radio en C. Une OC y DC para obtener △DOC. Dibuja los dos lados restantes de △COB y △BOA de la misma manera para obtener un cono trigonal con los lados expandidos.

La siguiente figura es un cono truncado, la longitud real del cono y la expansión, primero debe dibujar la parte superior del cono, convertirse en un cono completo y luego hacer una serie de superficies de cono y usar el método de rotación para encontrar estas líneas fueron truncadas parte de la longitud real de la línea (también está disponible para dejar parte de la longitud real de la línea), puede hacer la expansión de la figura.

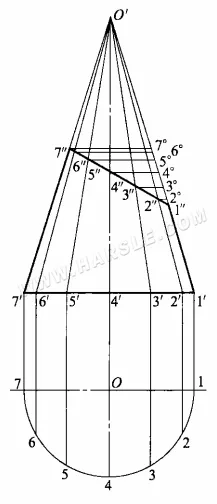
Para encontrar la longitud real de la parte truncada de la línea, los pasos de diagramación son los siguientes.

1. Extiende la línea de forma 1'1″ y 7'7″ para intersectar, dando como resultado la parte superior del cono O'.

2. Haz el círculo base del cono, y divide la circunferencia del círculo base en un número de partes iguales (aquí 1/2 de la circunferencia del círculo base se divide en 6 partes iguales), para obtener partes iguales 1, 2, …, 7, desde cada punto igual a la vista principal de la vertical, y la proyección ortogonal del círculo base intersecada en los puntos 1′, 2′, …, 7′, y luego desde cada punto y la parte superior del cono O' para la línea, para obtener el cono las líneas de la superficie cónica.

3. Entre las líneas del cono, solo las líneas de contorno 1″1′ y 7″7′ son paralelas a la proyección ortogonal y reflejan su longitud, mientras que las demás no reflejan la longitud real. El método consiste en trazar una línea paralela de 7″1′ desde 7″, 6″…, 2″ e intersecar la curva de nivel 0′1′ en 7°, 6°…, 2°, 0′6°, 0′5°…, 0′2° para 0′6″, 0′5″…, 0′2″, respectivamente. 2″ de longitud real.

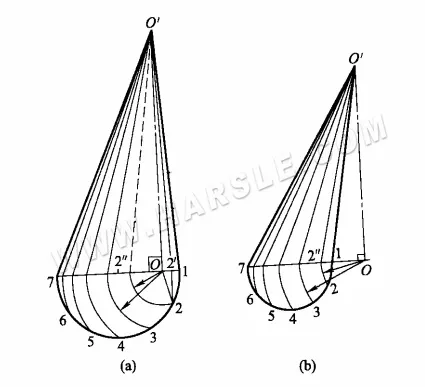
El diagrama anterior muestra la longitud real del cono oblicuo por rotación. Los pasos son los siguientes.

1. Primero divide la mitad del círculo base, es decir la circunferencia del círculo base en varias partes iguales (en el diagrama en 6 partes iguales).

2. con el pie vertical O como centro del círculo, O1, O2, …, O6 como radio del arco, y 1 ~ 7 intersección de líneas en 2 “y así en cada punto.

3. Traza una línea desde los puntos 2″, etc., hasta O', donde O'2′, etc., es la longitud real de la línea que pasa por los equinoccios. En otras palabras, O'2′ es la proyección ortogonal de la línea O2 y O'2″ es la longitud real de la línea O2.

El siguiente diagrama muestra las longitudes reales de los prismas de una articulación cuadrada utilizando el método de rotación y expansión de los mismos.

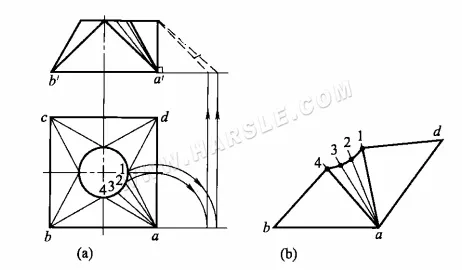
Los pasos para dibujar las longitudes reales de los prismas son

1. Dibuje la vista principal y la vista superior, compare la abertura del círculo de la vista superior y conecte las líneas simples correspondientes.

2. Gire las líneas simples a1, (a4), a2, (a3) y dibuje líneas verticales hacia arriba para derivar sus longitudes reales a-1, (a-4) y a-2, (a-3) en el lado derecho de la vista principal.

3. Utilizando las longitudes reales de las líneas simples, las longitudes de los bordes de la boca cuadrada y las longitudes de extensión de arco equivalentes de la boca redonda, dibuje las extensiones de 1/4 por turno.

Cuando la sección de transición del tubo cuadrado se encuentra frente al tubo redondo, debe haber una unión cuadrado-redonda. La boca cuadrada puede ser cuadrada o rectangular, y la boca redonda puede estar en el centro, a un lado o en una esquina. Por lo tanto, la forma de estas uniones puede variar, pero el método para determinar la longitud real de las uniones cuadrada y redonda es básicamente el mismo.

Método del triángulo rectángulo

El método del triángulo rectángulo es un método comúnmente utilizado para encontrar la longitud real.

El principio del método del triángulo rectángulo y el método de dibujo: el siguiente diagrama (a) es el diagrama principal del método del triángulo rectángulo para longitud real. El segmento AB no es paralelo al plano de proyección, y su proyección ab y a'b' no reflejan la longitud real. En el plano ABba, se traza una línea paralela a ab a través del punto A e interseca a Bb en el punto B1, dando como resultado el triángulo rectángulo ABB1. En este triángulo, la longitud real de la hipotenusa AB del triángulo rectángulo se puede encontrar conociendo las longitudes de los dos lados rectángulos AB1 y BB1. Y las longitudes de AB1 y BB1 se encuentran en el diagrama de proyección como AB1 = ab, BB1 = b'b1′ o BB1 = b'bx – a'ax. Conociendo estos dos lados rectángulos se dibuja de manera única el triángulo rectángulo buscado.

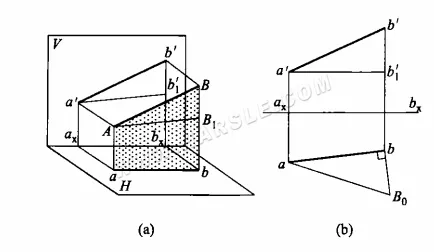
La figura (b) muestra el uso del método del triángulo rectángulo para determinar la longitud real. La proyección de la línea AB se conoce como ab y a'b'. Para determinar la longitud real de AB, primero se traza una línea horizontal que pasa por el punto a' y cruza la línea bb' en los puntos b1' y b1', es decir, la longitud de un lado recto del segmento. A continuación, se traza la vista superior de la línea ab para otro lado recto, sobre el punto b, una línea vertical y una intersección con bB0 = b'b1', conectada con aB0, es decir, la longitud real del segmento.

Ejemplo: El diagrama a continuación muestra una junta de boca cuadrada pequeña y grande, intente encontrar la longitud real de su línea principal AC y línea auxiliar BC.

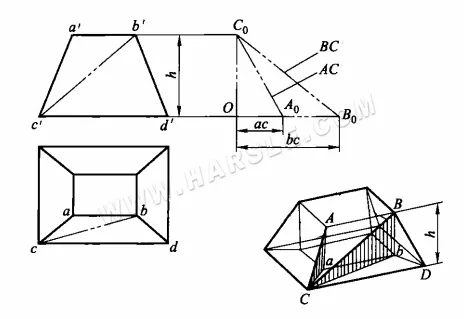
El diagrama muestra que la longitud real AC se encuentra en un triángulo rectángulo con aC y Aa como lados rectos, mientras que la longitud real BC se encuentra en el triángulo rectángulo BbC. En ambos triángulos, Aa = Bb = h, que es igual a la altura de la articulación. Los otros dos lados rectos aC y bC son iguales a las proyecciones ac y bc de AC y BC en la vista superior, respectivamente. De esta manera, las longitudes reales de AC y BC se pueden obtener como se indica a continuación.

1. Haz un ángulo recto B0OC0.

2. intercepta OA0 y OB0 en el lado horizontal de ese ángulo recto respectivamente igual a ac y bc en la vista superior, e intercepta OC0 en el lado vertical igual a la altura h en la vista principal.

3. conecta C0A0 y C0B0, entonces las hipotenusas C0A0 y C0B0 son las longitudes reales de los AC y BC solicitados.

El método del trapezoide de ángulo recto

El método del trapezoide rectángulo también es un método común para encontrar longitudes reales.

Principio del método del trapezoide rectángulo para longitudes reales y método de dibujo: el siguiente diagrama muestra el principio del uso del método del trapezoide rectángulo para longitudes reales. La ubicación general de la línea AB en las superficies V y H no puede reflejar la longitud real, pero los dos extremos de la línea AB y la distancia entre las superficies V se pueden obtener en la superficie H, es decir, Aa y Bb. Lo mismo, los dos puntos A, B y la distancia entre las superficies H también se pueden obtener en la superficie V, es decir, Aa y Bb. Con base en este principio, la longitud real de la línea AB se puede encontrar utilizando el método del trapezoide rectángulo. Hay dos métodos específicos para graficar las longitudes reales.

1. utilizando la proyección ortográfica de la longitud real de la recta AB: la proyección ortográfica de AB a'b' como el borde inferior del trapezoide rectángulo, desde a', b' dos puntos respectivamente hacia arriba de la recta vertical, intercepta la longitud de Aa', Bb', conectada a AB, es decir, para lo solicitado.

2. es el uso de la proyección horizontal de la longitud real del segmento de recta AB: la proyección horizontal de AB como el borde inferior de un trapezoide rectángulo, desde a, b dos puntos respectivamente hacia arriba de la recta vertical, intercepta la longitud de Aa, Bb, conecta AB que es el solicitado.

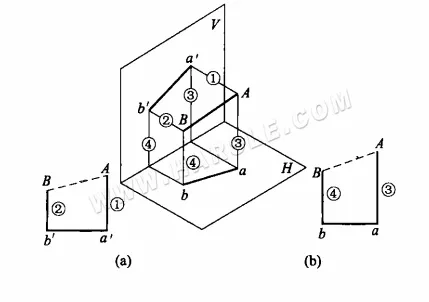
Ejemplo: La siguiente figura muestra una junta de deformación de herradura, su boca superior e inferior son círculos, pero los dos círculos no son paralelos ni iguales en diámetro, intente hacer un método de trapezoide en ángulo recto a partir de su longitud de línea y diagrama de expansión.

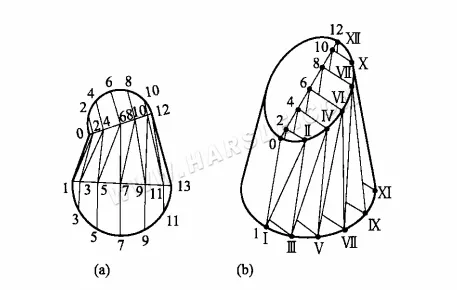
De la figura (a) anterior se desprende que, dado que su superficie no es cónica, para elaborar su diagrama de expansión solo se puede usar la línea que va y viene de la superficie en varios triángulos, y uno por uno para determinar la forma real de estos triángulos. Los pasos específicos para la graficación son los siguientes.

1. Haz 12 partes iguales de la boca superior e inferior y divide la superficie en 24 triángulos como se muestra en el diagrama.

2. Encuentra las longitudes reales de las líneas Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII, y luego construye la forma real de la serie de triángulos.

En estos ejemplos, si se utiliza el método de rotación o el método del triángulo rectángulo para determinar la longitud real, es necesario proyectar el segmento de línea en la vista superior. Dado que la superficie superior de la articulación de deformación en herradura y el plano de proyección horizontal están inclinados, la superficie superior en la vista superior se refleja como una elipse. Obviamente, estos dos métodos para la expansión del mapa presentan mayores dificultades, por lo que resulta apropiado utilizar el método del trapezoide rectángulo.

Como se muestra en la figura (b), la superficie plegada Ⅰ-1-Ⅱ-2-Ⅲ-3…XII-12 se extiende a la figura que se muestra a continuación, y luego a la figura sobre la línea de pliegue Ⅰ-Ⅱ-Ⅲ…XII, es decir, las longitudes reales Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII, y así sucesivamente. Este método para calcular las longitudes reales se denomina método del trapezoide rectángulo.

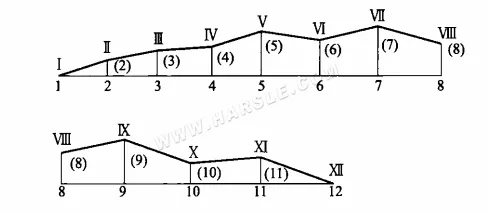
Como se puede observar en el método de diagramación, el método del trapezoide rectángulo también se basa en la proyección de una línea inclinada como base, con la distancia de los dos extremos de la línea inclinada desde el mismo plano de proyección que los dos lados rectos. Tras formar un trapezoide rectángulo, se obtiene la hipotenusa del trapezoide rectángulo, es decir, la longitud real de la línea solicitada. El triángulo rectángulo puede considerarse un caso especial del método del trapezoide rectángulo, donde la longitud del lado recto es igual a cero.

El método anterior se utiliza para obtener las dos líneas laterales de cada triángulo en la superficie de la junta de deformación en herradura, cuyo otro lado es la longitud de las aberturas circulares superior e inferior, igual al arco desplegado. De esta manera, se puede formar una serie de triángulos mediante el método de triángulos con tres lados conocidos, que se disponen para obtener el siguiente diagrama de la junta de deformación en herradura.

Método de cambio de cara

Además de los métodos anteriores para encontrar la longitud real de la línea, también existe el método común de cambiar la superficie.

El principio del método de cambio de superficie para la longitud real y el método de dibujo: El principio del método de cambio de superficie consiste en mantener el segmento espacial sin cambios y crear una nueva superficie de proyección para que sea paralela al segmento solicitado y perpendicular a la original. La proyección del segmento sobre la nueva superficie de proyección reflejará su longitud real. El diagrama anterior muestra un diagrama esquemático de la longitud real de un segmento de línea.

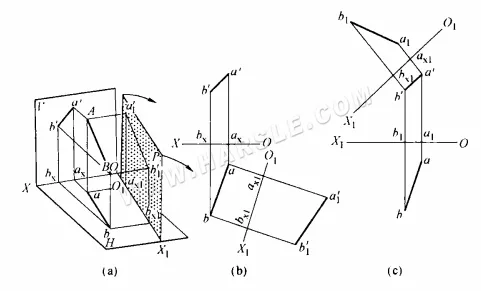
Como se puede observar en el diagrama anterior (a), el segmento AB no es paralelo a los planos de proyección H y V, y su proyección no refleja la longitud real. La nueva proyección a1'b1' refleja la longitud real de AB. Un análisis más detallado del espacio mostrado en la figura (a) revela las siguientes relaciones de proyección para el método de cambio de superficie.

1. Dado que la nueva superficie de proyección P es paralela a AB y perpendicular al plano H, entonces la línea de intersección entre la nueva superficie de proyección P y el plano H, O1X1 (llamada el nuevo eje de proyección), es necesariamente paralela a la proyección del plano H ab de la línea AB, O1X1 // ab, como se refleja en la proyección del plano H.

2. Puesto que las superficies P y V son simultáneamente perpendiculares a la superficie H, la distancia desde la proyección a1'b1' de la superficie P a O1X1 y la distancia desde la proyección a'b' de la superficie V a OX deben reflejar simultáneamente las distancias perpendiculares desde los dos puntos finales A y B de la línea espacial a la superficie H, y son iguales entre sí, a1ax1 = a'ax = Aa y b1'bx1 = Bb. Para facilitar la designación, la proyección recién hecha paralela a AB La proyección a1'b1' que refleja la longitud real se llama la nueva proyección, la proyección a'b' que originalmente no reflejaba la longitud real se llama la proyección antigua o de reemplazo, y la proyección del plano H que es perpendicular a ellas al mismo tiempo se llama la proyección invariante. De esta manera, esta relación de proyección para el método de superficie de reemplazo se puede expresar como la distancia desde la nueva proyección al nuevo eje que es igual a la distancia desde la proyección antigua al eje antiguo.

3. Dado que las superficies P y V son perpendiculares a la superficie H, la conexión entre la proyección P y la proyección H en cualquier punto de la línea debe ser perpendicular al nuevo eje de proyección O1X1, la línea entre la proyección invariante y las proyecciones antigua y nueva es perpendicular a los ejes de proyección antiguo y nuevo respectivamente, después del despliegue.

De acuerdo con la relación de proyección anterior del método de permutación, los pasos de graficación deben ser

1. como se muestra en (b) arriba, haga que el nuevo eje de proyección O1X1 sea paralelo a ab.

2. Dibuje una línea perpendicular a través de los puntos a y b hasta el eje O1X1 e interseca O1X1 en los puntos ax1 y bx1.

3. Mueva las proyecciones a' y b' del plano V al eje OX al nuevo plano de proyección, mida ax1a1'=axa' y bx1b1'=bxb' en las líneas verticales.

4. Une los puntos a1′ y b1′, la nueva proyección a1'b1′ de la recta AB, que refleja la longitud real de AB.

Ejemplo: El diagrama a continuación muestra el uso del método del plano de proyección auxiliar para encontrar la forma real de una sección cilíndrica.

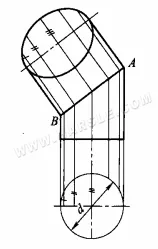
Los pasos del dibujo son los siguientes.

1. Haz una vista principal y superior, dividiendo la vista superior por la mitad de la circunferencia del círculo en 6 partes iguales.

2. Dibuje una línea vertical hacia arriba a través del punto equidistante para indicar la posición de la línea principal en la vista principal.

3. Dibujar perpendiculares hacia abajo desde los puntos equidistantes para intersecar la línea central inferior, el ancho entre las líneas simples de la sección.

4. dibujar líneas perpendiculares a través de la intersección de las líneas en la abertura oblicua de la sección hasta el eje largo paralelo a la abertura oblicua de la sección, y luego dibujar la distancia entre los puntos equidistantes en la vista superior y la línea central del círculo inferior, a su vez, hasta los puntos en la vista secundaria, de acuerdo con la regla de “ancho igual”.

5. Conecta los puntos para crear una elipse sólida de la sección.

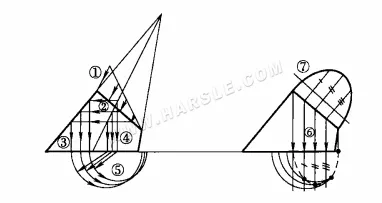
El diagrama a continuación muestra el uso del método del plano de proyección auxiliar para determinar la forma real de la sección del ortocono. Los diagramas ①, ②, … (7) indican el orden de trazado y las líneas de conexión.

En general, no es necesario dibujar líneas en la superficie del cono para representar la forma real de la sección cónica, pero es mejor usar el método del círculo de trama, como se muestra en la figura anterior. Para que las líneas sean más claras, en este ejemplo se dibujarán por separado los tres pasos del diagrama; no es necesario separar el diagrama real. Los pasos son los siguientes.

1. Círculos de trama: la línea de proyección de la sección se divide en 6 partes iguales; la línea horizontal de los puntos iguales anteriores se interseca con la línea de contorno; la línea vertical se dibuja hacia abajo desde cada punto de intersección en la línea de contorno y se interseca en la parte inferior del cono; los círculos de trama se dibujan a su vez con el centro del círculo O, véase la figura (a) anterior.

2. Vista superior de la sección transversal: al trazar una línea vertical hacia abajo a través de cada equivoco de las líneas de la sección transversal en la vista principal, intersectando con el círculo de latitud correspondiente, se obtiene una serie de puntos de intersección; al conectar los puntos de intersección, se puede obtener la proyección de la vista superior de la sección transversal, consulte la figura (b) anterior.

3. Para determinar la forma real de la sección: dibuje una elipse paralela al eje longitudinal de la sección (1″7″); trace líneas perpendiculares desde cada punto igual de la sección (1~7) hasta el eje longitudinal (1″7″); siguiendo el principio de igualdad de anchos, dibuje una serie de anchos (a, b, c, d y e) de la sección en la vista superior hacia la proyección auxiliar, resultando en puntos de 2″, 3″, 4″, 5″ y 6″; conecte los puntos, es decir, la forma real de la sección cónica (véase el diagrama (b) arriba). Figura (c) arriba.

El diagrama a continuación muestra el uso del método de superficie de proyección auxiliar para encontrar la forma real de la sección cónica oblicua.

El uso de la vista auxiliar para la forma real de la sección cónica oblicua es similar al de la forma real de la sección cónica ortogonal. Sin embargo, el cono oblicuo tiene la característica de que su vértice está inclinado hacia un lado y su eje también lo está, de modo que el centro de una serie de círculos de trama no se encuentra en el mismo punto del mismo eje. Por lo tanto, en lugar de crear círculos concéntricos, se crea un cono con un centro para cada círculo de trama. Esta característica se puede dominar siguiendo los tres pasos descritos anteriormente para dibujar la vista auxiliar de una sección sólida.

Los pasos específicos del dibujo son los siguientes.

1. Para el círculo de trama: la línea de sección 4 partes iguales; para puntos iguales de la línea horizontal, intersectando con la línea de contorno; desde la línea de contorno en los puntos hacia abajo hasta la línea vertical, intersectando con el círculo inferior; puntos iguales de la línea horizontal y el eje de intersección de los puntos para el círculo de trama del centro, el centro del círculo al círculo inferior; respectivamente, el centro del círculo de trama y el radio correspondiente para el círculo de trama.

2. Vista superior de la sección: a través de la vista principal de las líneas de sección de cada equivoco, líneas verticales descendentes y la intersección del círculo de latitud correspondiente, resultando en una serie de puntos de intersección; junto con los puntos de intersección, puede obtener la vista superior de la proyección de la sección.

3. Para hacer la forma real de la sección: de acuerdo con el ancho de la forma de la sección que se encuentra en la vista superior, haga 1/2 vista auxiliar para dibujar la forma real 1/2 de la sección cónica oblicua.

Comparación de métodos de longitud real

Con base en el análisis anterior, se puede hacer una comparación simple entre los cuatro métodos para encontrar la longitud real de una línea real.

El método de rotación resuelve la longitud real cambiando la posición de la figura en el espacio, sin cambiar la posición del plano de proyección.

El método de permutación resuelve la longitud real cambiando la posición del plano de proyección sin cambiar la posición de la figura.

El método del triángulo rectángulo y el método del trapezoide rectángulo (el método del triángulo rectángulo puede considerarse un caso especial del método del trapezoide rectángulo) resuelven la línea de longitud real sin cambiar ni la posición de la figura espacial ni la posición del plano de proyección.