Predicción del radio de flexión interior al utilizar una prensa plegadora
A medida que profundizo en el tema de la predicción Curvatura de radio interior Al usar una prensa plegadora, he descubierto que comprender las complejidades de este proceso puede influir significativamente en la calidad de nuestros proyectos de fabricación de metal. El radio interior es crucial para garantizar plegados precisos y lograr los resultados deseados. En este artículo, compartiré conocimientos y técnicas que me han ayudado a predecir eficazmente el radio interior al usar una prensa plegadora, mejorando así la eficiencia y la precisión de nuestras operaciones. ¡Acompáñenme a explorar este aspecto esencial de la metalurgia!
Predecir el radio nunca es 100 por ciento exacto, pero esto es lo mejor que se puede conseguir.
Puede utilizar algunas reglas generales para predecir el radio de curvatura interior al realizar el conformado por aire, y los resultados que obtiene suelen ser bastante cercanos, pero con la ayuda de algunas calculadoras en línea, puede acercarse aún más.
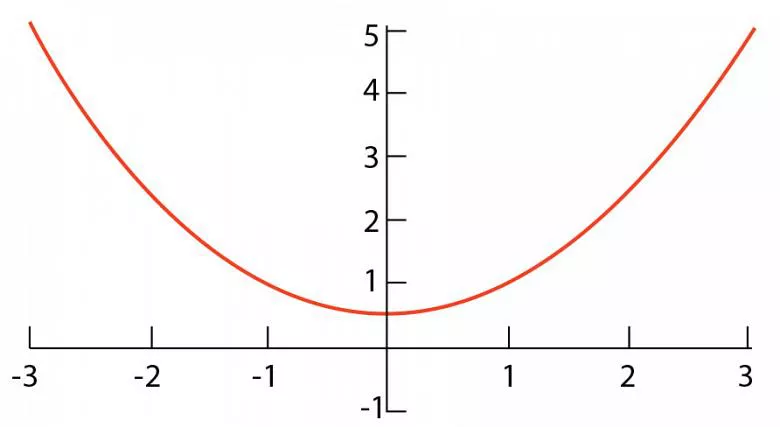
Muchas veces, durante el formado, no estamos formando un radio verdadero, sino una parábola.
Si ha estado siguiendo en los últimos meses nuestra discusión sobre radio de curvatura Y de dónde viene, bienvenido de nuevo. En cualquier caso, veamos qué tan profundo es este agujero del radio.
En artículos anteriores, he analizado varias reglas generales que los operadores usan en el taller para realizar su trabajo. Estas reglas pueden aproximar la predicción del radio de curvatura interior, pero usted puede aproximarse aún más.
¿Qué diferencia hay?
Considere una situación típica en la que se utiliza la regla del 20 por ciento, que establece que un radio doblado al aire se forma como un porcentaje de la apertura de la matriz, del 20 al 22 por ciento para el acero inoxidable y aproximadamente el 16 por ciento para el acero laminado en frío de 60 KSI, nuestro material de base.
Supongamos que dobla aluminio blando de 13 KSI con un ancho de matriz de 0,984 pulgadas y un punzón con un radio de 0,032 pulgadas. Como punto de partida, calcula que el radio de curvatura interior al 16 % de la abertura de la matriz es de 0,157 pulgadas, aunque esto es para material de 60 KSI, por lo que deberá adaptarse al tipo de material. Mientras tanto, al calcular si la curva se volverá cerrada, descubre que el radio mínimo antes de que el punzón de 0,032 pulgadas comience a marcar la línea de curvatura es de 0,172 pulgadas. Finalmente, realiza un doblez de prueba, solo para descubrir que el radio real es de 0,170 pulgadas.
Tienes el radio de 0,157 pulgadas calculado con la regla del 20%, y luego el radio de 0,172 pulgadas calculado con los cálculos de curvatura cerrada. Esa es una diferencia de radio de 0,015 pulgadas. ¿No es mucho? En este caso, la diferencia al aplicar la deducción por curvatura puede alcanzar 0,009 pulgadas por curva.
¿Alguna vez has construido una pieza con cuatro bridas laterales y cuatro bridas adicionales en la parte superior, solo para descubrir que una esquina queda perfecta, dos esquinas son marginalmente satisfactorias y una se ve horrible? ¿Por qué sucede esto? Un pequeño error en la deducción del pliegue, causado por discrepancias en los cálculos del radio de pliegue interior, marca una gran diferencia si quieres piezas perfectas a la primera.
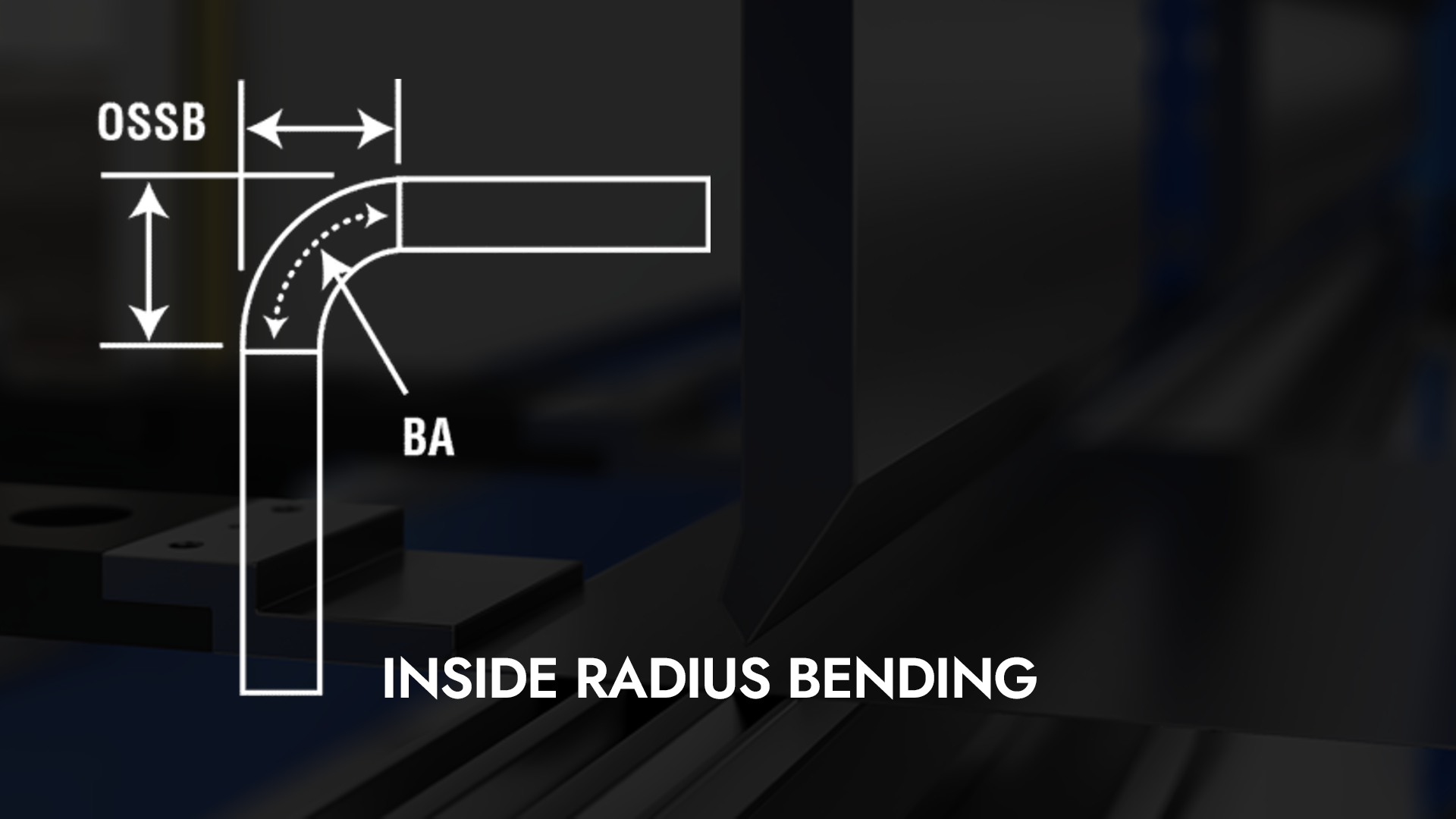
La clave de cualquier operación de plegado es el radio interior de la curva. Si se puede calcular la deducción por curvatura basándose en los resultados reales, se garantiza la precisión. El único fallo de esta teoría es que, a menudo, durante el conformado no se forma un radio real. La forma que se forma puede ser una parábola, una curva simétrica reflejada, generalmente en forma de U al orientarse como se muestra en la Figura 1. El radio final que se obtiene es el resultado de la recuperación elástica.
- Efectos de recuperación elástica
Entonces, ¿cómo predecimos el radio de curvatura interior más preciso y la deducción correcta del doblez? Para lograrlo manualmente, las matemáticas son complejas, así que no entraré en detalles. En su lugar, simplemente usaremos dos calculadoras web diferentes.
El primero está en www.harsle.com. Haga clic en la Calculadora completa de arcos circulares. Tenga en cuenta que la etiqueta Ancho del arco en la calculadora coincide con el ancho de la matriz, y que el Ángulo subtendido por el arco coincide con el ángulo de plegado incluido.
Asegúrese de que la configuración de dimensiones de la calculadora sea correcta para los datos que está utilizando (pulgadas, pies, milímetros, etc.). Tenga en cuenta que cuando hacemos clic en Entrar, las respuestas que obtenemos son puramente matemáticas y no se han tenido en cuenta para la resistencia a la tracción del material.
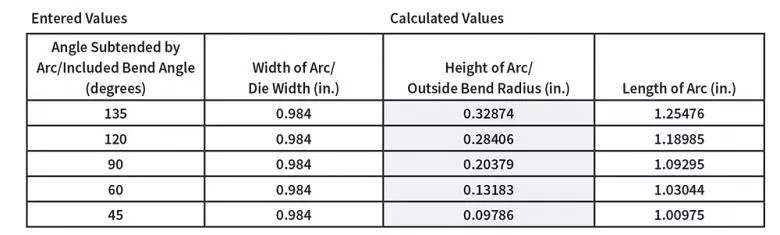
Como se muestra en este cálculo de The Complete Circular Arc Calculator en www.harsle.com, a medida que aumenta el ángulo de curvatura incluido, también lo hace el radio (altura del arco).
La información que buscamos en la calculadora es la altura del arco, que equivale al radio de curvatura exterior. Encuentremos un valor para nuestra referencia: acero laminado en frío de 60 kSI, de 0,125 pulgadas de espesor, con un ancho de matriz de 0,984 pulgadas. Tenga en cuenta que se trata de conformado por aire, por lo que el ángulo de la matriz no influirá; puede ser una matriz de canal, aguda o en V. Lo que importa es el ancho.
Primero, entremos en el ángulo relajado: esos 90 grados que queremos lograr.
Valores ingresados
Ángulo subtendido por el arco (ángulo de curvatura incluido): 90 grados
Ancho del arco (ancho de matriz): 0,984 pulg.
Valor calculado
Altura del arco (radio de curvatura exterior): 0,20379 pulg.
Sin embargo, estos cálculos no consideran la recuperación elástica. En nuestro ejemplo, usaremos un valor de 1 grado para la recuperación elástica, que se produce cuando tenemos una relación aproximada de 1 a 1 entre el espesor del material y el radio de curvatura interior. Después de que el punzón libera la presión de conformado, el material recupera elásticamente 1 grado; por lo tanto, para compensar, ahora usamos un ángulo de curvatura de 89 grados incluido. De nuevo, utilizando la Calculadora Completa de Arco Circular en harsle.com, ingresamos lo siguiente:
Valores ingresados
Ancho del arco (ancho de matriz): 0,984 pulg.
Ángulo subtendido por el arco (ángulo de curvatura incluido): 89 grados
Valor calculado
Altura del arco (radio de curvatura exterior): 0,201 pulg.
Ahora tomamos el valor de la Altura del Arco para nuestro nuevo ángulo de curvatura y lo introducimos en la siguiente fórmula:
Altura del arco – (2 × Espesor del material2) = Radio interior
0,201 – (2 × 0,01562) = Radio de curvatura interior
0,201 – 0,031 = 0,170 pulgadas de radio de curvatura interior
Tenga en cuenta que este enfoque de la altura del arco es diferente al utilizado en la columna Fundamentos de plegado del mes pasado, cuando utilizamos la longitud del arco. El mes pasado calculamos un radio interior basado en el ancho de la abertura de la matriz; esta vez, utilizamos un radio específico.
El mes pasado calculamos un radio de 0,136 pulgadas, y ahora mismo calculamos el radio interior con un método diferente y obtuvimos 0,170 pulgadas, una diferencia de 0,034 pulgadas. Además, si usáramos la regla del 20 % (de nuevo, para el acero laminado en frío de 60 kSI, el radio se calcula aproximadamente en el 16 % del ancho de la matriz), obtendríamos un radio interior de 0,157 pulgadas, un valor intermedio entre las dos mediciones anteriores. Todas estas son maneras diferentes de calcular el radio, con resultados ligeramente distintos. Pero sí, ¡el problema se profundiza!
- Parábola y curvas cerradas
Si utiliza un valor de radio de punzón igual o menor que el radio de curvatura pronunciada mínimo para el conformado de una pieza con aire, ya no estará creando un radio en la pieza (para obtener más información sobre curvaturas pronunciadas, En su lugar, estará creando una parábola. En efecto, está introduciendo una longitud de arco diferente en la abertura de la matriz.
Para predecir cómo se formará esta parábola, podemos recurrir a otra calculadora en línea:
Introducimos el radio exterior y el ancho de la matriz para calcular la longitud del arco de la parábola. El valor de la altura en esta calculadora en línea equivale al radio de curvatura exterior, mientras que el valor del ancho equivale al ancho de la matriz.
Valores ingresados
Altura: (radio exterior): 0,201 pulg.
Ancho (ancho de matriz): 0,984 pulg.
Valor calculado
Longitud del arco: 1,0845 pulg.
Aquí, la profundidad de la parábola (o altura del arco) es de 0,201 pulgadas y la longitud del arco es de 1,0845 pulgadas. Recuerde estos valores. Volviendo a la Calculadora Completa de Arcos Circulares en www.harsle.com, ingresamos la longitud del arco en 1,0845 pulgadas y el ancho de la matriz en 0,984 pulgadas.
Valores ingresados
Longitud del arco: 1,0845 pulg.
Ancho del arco (ancho de matriz): 0,984 pulg.
Valores calculados
Altura del arco (radio de curvatura exterior): 0,195 pulg.
Ángulo subtendido por el arco
(ángulo de curvatura incluido): 86,679 grados
Al hacer esto, verá que la altura del arco (es decir, el radio exterior) es de 0,195 pulgadas, un poco menor que el radio exterior de 0,201 pulgadas de la calculadora anterior, que no tuvo en cuenta el efecto de la parábola. Sabiendo esto, podemos afirmar con seguridad que el radio interior disminuye cuando se forma una parábola, lo que ocurre al utilizar un radio de punzón menor que el radio mínimo de curvatura cerrada. Tenga en cuenta que la parábola también requiere un mayor ángulo de curvatura para producir el ángulo de curvatura relajado deseado; pasamos de un ángulo de curvatura incluido de 89 a 86,68 grados, lo que supone 2,32 grados adicionales de recuperación elástica. Tenga en cuenta también que el radio interior de la pieza no será menor que el radio de la punta del punzón.
- Ángulos y radios de curvatura
Recuerde que cualquier cambio en el radio implica un cambio en el ángulo de plegado. Si ingresamos el ancho de la matriz y el ángulo de plegado en www.harsle.com, obtenemos los resultados que se muestran en la Figura 2.
Los resultados muestran que cuando se forma el aire, el radio disminuye con el ángulo de curvatura incluido (curvas cerradas excluidas).
Esta relación ángulo/radio de curvatura se detiene en ángulos incluidos menores a 28 grados incluidos (152 grados complementarios), aunque el ángulo mínimo incluido puede ser mayor en materiales con una recuperación elástica significativa.
Esto se debe en parte a que el ángulo mínimo de punzón de la plegadora es de 28 grados. Dicho esto, si se continúa cerrando el pliegue más allá de los 28 grados, se producirá algún tipo de aplanamiento. El radio se reducirá hasta que se alcance el ángulo de pliegue deseado o se complete el engatillado. (A modo de apunte, para un engatillado cerrado, el radio es cero y la deducción por pliegue se calcula como un porcentaje del espesor del material: 43 % en condiciones ideales, aunque es una operación muy dependiente del operador).
- Factorización de la resistencia a la tracción
En el ejemplo anterior, utilizamos 1 grado de recuperación elástica para realizar los cálculos. Para el acero dulce laminado en frío de 60 kSI, la recuperación elástica promedio es de 1 grado o menos. ¿Qué ocurre con otros materiales?
Para ello, podemos predecir la recuperación elástica con un grado de precisión razonable utilizando la siguiente fórmula, que requiere convertir todos los valores al sistema métrico. Tenga en cuenta que predecir la recuperación elástica nunca es 100% preciso. Sin embargo, estas fórmulas son bastante eficaces.
[(Radio interior en milímetros/2)/
Espesor del material en milímetros] × Factor de tracción
Factor de tracción = Resistencia a la tracción del material en PSI/60 000
Primero, calculemos la recuperación elástica como si estuviéramos trabajando con nuestro material de base de 60 KSI con un radio de curvatura interior de 0,170 pulgadas:
[(Radio interior en milímetros/2)/
Espesor del material en milímetros] × Factor de tracción
Espesor del material: 0,125 pulg. × 25,4 = 3,175 mm
Radio de curvatura interior: 0,170 pulg. × 25,4 = 4,318 mm
(4.318/2) /3.175
2,159 mm / 3,175 mm = 0,68 grados de recuperación elástica
En este ejemplo, redondearemos esto a 1 grado. Luego, podemos aplicar el factor de tensión para el acero inoxidable 304 de 88-KSI.
Factor de tracción = Resistencia a la tracción del material en PSI/60 000
88,000/60,000 = 1.466666
1,0 grados × 1,466666
Esto nos da 1,46 grados para el acero inoxidable 304 de 88-KSI. Redondeando hacia arriba, esto nos da 1,5 grados de recuperación elástica estimada con una relación de 1 a 1 entre el radio interior y el espesor del material.
- Volver a la calculadora
Ahora que puede estimar la recuperación elástica con un nivel de precisión razonable, puede compensarla. Para determinar el ángulo necesario para compensar la recuperación elástica, simplemente reste el valor de la recuperación elástica si trabaja con ángulos de curvatura incluidos, o sume ese valor si utiliza ángulos de curvatura complementarios. La calculadora de arco circular en www.harsle.com funciona con ángulos de curvatura incluidos (de nuevo, denominados "Ángulo de arco subtendido").
Una vez que conozca el radio interior (es decir, el radio interior real que aparecerá en la pieza terminada), puede insertar ese valor de radio en sus fórmulas de doblado (ver barra lateral).
Conclusión
Al predecir correctamente el radio interior, podemos calcular con precisión las deducciones por curvatura. De las diversas maneras de predecir el radio interior, ninguna es perfecta, pero esta es prácticamente la mejor. Aun así, la curvatura tiene demasiadas variables para lograr una precisión del 100 %.
También es fundamental, en el conformado por aire, que el ingeniero o programador informe al técnico sobre los conjuntos de herramientas con los que se diseñó cada curva. Además, el técnico debe comprender la importancia fundamental de usar dichas herramientas para lograr piezas de calidad.
El próximo mes veremos cómo calcular el radio interior de los pliegues donde la relación entre este y el espesor del material es muy grande: el pliegue de radio profundo. Los pliegues de radio grande presentan problemas con el ángulo y el ancho de la matriz, la multirrotura y, por supuesto, una recuperación elástica muy alta.
El agujero del conejo todavía tiene un largo camino por recorrer, pero vale la pena el viaje.
Una revisión de las fórmulas de flexión
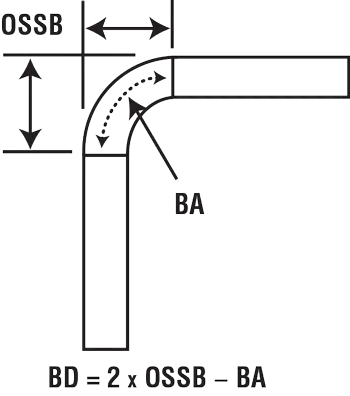
Estas fórmulas para tolerancia de curvatura, retroceso exterior y deducción de curvatura están bien establecidas, y cada valor se puede usar de diferentes maneras para calcular la disposición de la pieza en bruto plana.
Fórmulas
BA = [(0,017453 × Rp) + (0,0078 × Mt)]
× Grados de curvatura complementarios
OSSB = [Tangente (grado de ángulo de curvatura/2)]
× (Mt + Rp)
BD = (OSSB × 2) – BA
Llave
Rp = Radio de la punta del punzón (fondo)
o el radio interior flotado (formación de aire)
Mt = Espesor del material
BA = Margen de curvatura
BD = Deducción por curvatura
OSSB = Retroceso exterior
0,017453 = π/180
0,0078 = factor K × π /180
Factor K = 0,446











America-Customer-Feedback-1.jpg)
America-Miami-Customer-Feeback-1.jpg)
Uzbekistan-Customer-Feedback1.png)
Kosovo-Customer-Feedback11.png)
Russia-Customer-Feedback.jpg)
Russia-Customer-Feedback-3.jpg)




