En mi experiencia trabajando con doblado de ranurasCalcular la longitud desplegada es esencial para obtener resultados precisos en la fabricación de metal. Esta longitud determina la cantidad de material necesario antes del doblado, y realizar este cálculo correctamente es crucial para evitar desperdicios y garantizar un ajuste adecuado. A lo largo de los años, he desarrollado un enfoque sistemático para calcular la longitud desplegada En este artículo, compartiré mis conocimientos sobre cómo calcular la longitud desplegada del doblado de ranuras, brindando consejos prácticos que pueden mejorar la precisión del doblado en diversas aplicaciones.

Comprensión de la flexión de ranuras

Antes de profundizar en los cálculos, es importante comprender qué implica el doblado con ranuras. Este proceso implica crear una ranura a lo largo del material para facilitar el doblado en un ángulo específico. La ranura suele ayudar a controlar el doblado y a garantizar un plegado más limpio y preciso. Sin embargo, para lograr el ángulo y la forma deseados, es necesario conocer la longitud correcta del material sin doblar.

La fórmula para la longitud desplegada

Como se muestra en la figura, ahora se utiliza el cepillado para doblar un tubo cuadrado de 20 × 20 con un espesor de placa de 1 mm.

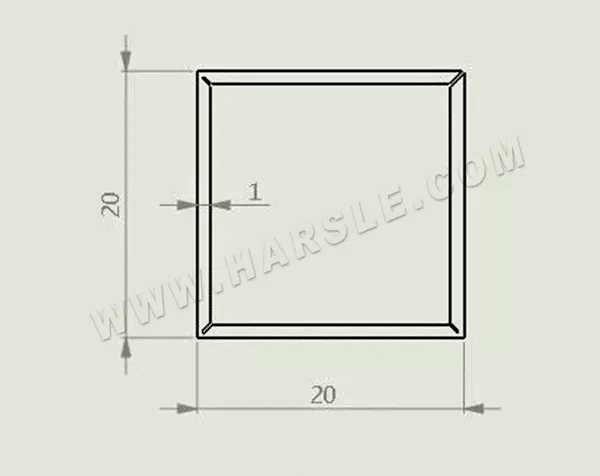
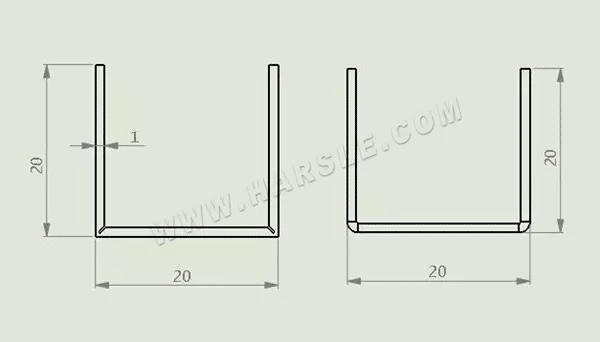
El espesor restante del material a de la ranura de cepillado está relacionado con el tamaño del arco en ángulo recto después del doblado por el cliente, así como con el espesor del material t. En general, cuando el espesor del material es menor o igual a 1 mm, a = 0,4 mm, y cuando es mayor a 1 mm, a = t/2.

L=2×(L1+L2)=2x((longitud del lado-1xa-0,2)+(longitud del lado-2xa)) del ejemplo ilustrado

=2x((20-1×0,4-0,2)+(20-2×0,4))=77,2 mm

Nota: Se cepilla un extremo de L1, sin importar el grosor del material, se deducen 0,2 mm.

Comparemos la diferencia entre el cálculo de flexión y desplegado mediante flexión ranurada y flexión no ranurada:

Para curvas ranuradas, el método para calcular la longitud total es:

L=20-0,4+20-2X0,4+20-0,4=58,4

Para curvas sin ranuras, el método para calcular la longitud total es:

●L=(20-1xt+k)+(20-2xt+2xk)+(20-1xt+1xk)=(20-1+0,2)+(20-2+2×0,2)+(20-1+ 0,2)=56,8 mm

●t es el espesor del material, k es el coeficiente, el tamaño de k está relacionado con el espesor del material, generalmente entre 0,2-0,25, cuanto más grueso sea el material, mayor será el valor K. En este ejemplo, k se selecciona como 0,2.

La siguiente es una combinación de una ranura en forma de Z y ninguna ranura para calcular la longitud desplegada de la curva:

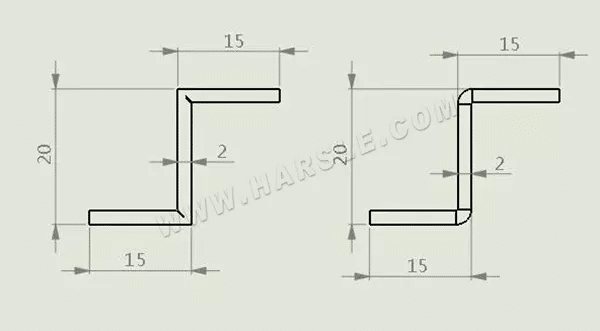
Para el tablero de 2 mm, el espesor del material restante a de la ranura de cepillado se toma como t/2 = 1 mm (si el cliente requiere que el arco directo sea más pequeño, el valor a debe seleccionarse menor a 1 mm), por lo que la longitud de expansión:

L=15-1+20-2×1+15-1=46 mm

Para un tablero de 2 mm de espesor, sin ranurar ni doblar, el coeficiente k se selecciona como 0,25, por lo que la longitud desplegada:

L=(15-2+0,25)+(20-2×2+2×0,25)+(15-2+0,25)=43mm

A continuación se describe el método de cálculo con un ejemplo de ranurado y no ranurado de una pieza de trabajo con múltiples curvas:

Para la placa de 3 mm de espesor, se supone que el cliente requiere que el arco de ángulo recto sea más pequeño, entonces el espesor del material restante es de 0,5 mm y la longitud expandida L = (40-0,5) + (30-2 × 0,5) + (30-2 × 0,5) + (10-0,5) = 107 mm;

Para una placa de 3 mm de espesor, el coeficiente k se selecciona como 0,25, por lo que la longitud desplegada:

L=(40-3+0,25)+(30-6+2×0,25)+(30-6+2×0,25)+(10-3+0,25)=93,5 mm

A continuación se muestra un ejemplo de flexión inversa después del ranurado para presentar el método de cálculo de la expansión:

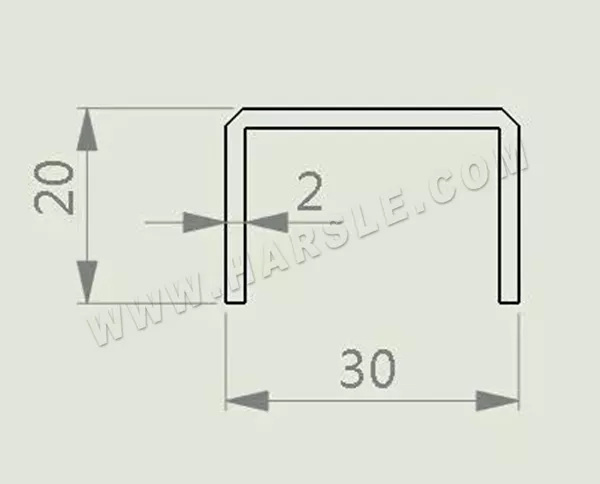
Para curvas hacia atrás después de ranurar como se muestra

Calcular la longitud de la expansión como

L=(20-2+0,2)+(30-2×2+2×0,2)+(20-2+0,2)=62,8 mm