Previsione della piegatura del raggio interno quando si utilizza una pressa piegatrice
Mentre approfondisco l'argomento della previsione Curvatura del raggio interno Utilizzando una pressa piegatrice, ho scoperto che comprendere le complessità di questo processo può avere un impatto significativo sulla qualità dei nostri progetti di lavorazione dei metalli. Il raggio interno gioca un ruolo cruciale nel garantire piegature precise e ottenere i risultati desiderati. In questo articolo, condividerò spunti e tecniche che mi hanno aiutato a prevedere efficacemente il raggio interno durante l'utilizzo di una pressa piegatrice, migliorando sia l'efficienza che la precisione delle nostre operazioni. Unitevi a me per esplorare questo aspetto essenziale della lavorazione dei metalli!
Prevedere il raggio non è mai accurato al 100%, ma questo è il massimo che si possa ottenere.
È possibile utilizzare alcune regole pratiche comuni per prevedere il raggio di curvatura interno durante la formazione dell'aria; i risultati ottenuti sono solitamente abbastanza precisi, ma con l'aiuto di alcuni calcolatori online è possibile avvicinarsi ancora di più.
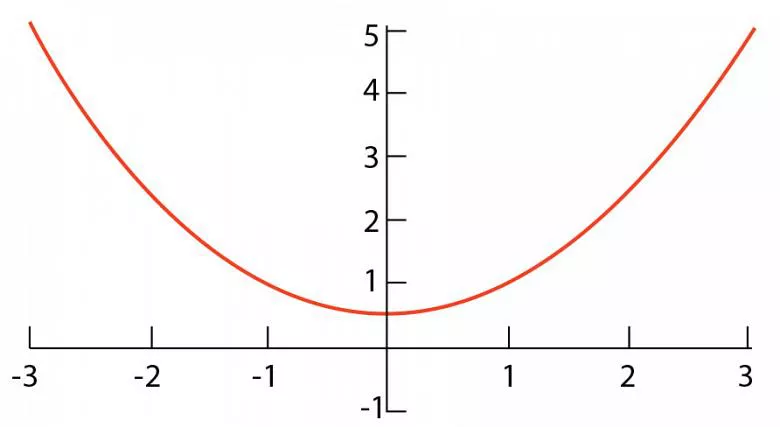
Spesso durante la formazione non si forma un vero raggio, bensì una parabola.
Se avete seguito negli ultimi mesi la nostra discussione su raggio di curvatura E da dove viene, bentornati. In ogni caso, vediamo quanto è profonda questa tana del Bianconiglio.
In articoli precedenti ho discusso diverse regole pratiche che gli operatori utilizzano in officina per portare a termine il lavoro. Queste regole possono aiutarti a prevedere il raggio di curvatura interno in modo più preciso, ma puoi anche avvicinarti ancora di più.
Che differenza fa?
Consideriamo una situazione tipica in cui si utilizza la regola del 20 percento, che stabilisce che il raggio di curvatura in aria si forma come percentuale dell'apertura della matrice, dal 20 al 22 percento per l'acciaio inossidabile e circa il 16 percento per l'acciaio laminato a freddo 60-KSI, il nostro materiale di base.
Supponiamo di piegare alluminio morbido da 13 KSI con una matrice da 0,984 pollici e un punzone con raggio di 0,032 pollici. Come punto di partenza, calcoli che il raggio di piegatura interno al 16% dell'apertura della matrice sia di 0,157 pollici, sebbene questo sia per un materiale da 60 KSI, quindi dovrai adattarlo al tipo di materiale. Nel frattempo, quando calcoli per vedere se la piega diventerà stretta, scopri che il raggio minimo prima che il tuo punzone da 0,032 pollici inizi a piegare la linea di piega è di 0,172 pollici. Infine, esegui una piegatura di prova, solo per scoprire che il raggio effettivo è di 0,170 pollici.
Hai il raggio di 0,157 pollici calcolato con la regola del 20%, poi hai il raggio di 0,172 pollici dai calcoli delle curve strette. Questa è una differenza di raggio di 0,015 pollici. Non molto, dici? In questo caso, la differenza, applicata alla detrazione per curvatura, può raggiungere 0,009 pollici per curva.
Hai mai costruito un componente con quattro flange laterali e quattro flange aggiuntive lungo la parte superiore, per poi scoprire che un angolo è perfetto, due sono appena soddisfacenti e uno è orribile? Perché succede questo? Un piccolo errore nella deduzione della curvatura causato da discrepanze nei calcoli del raggio di curvatura interno fa una grande differenza se vuoi componenti perfetti fin dal primo tentativo.
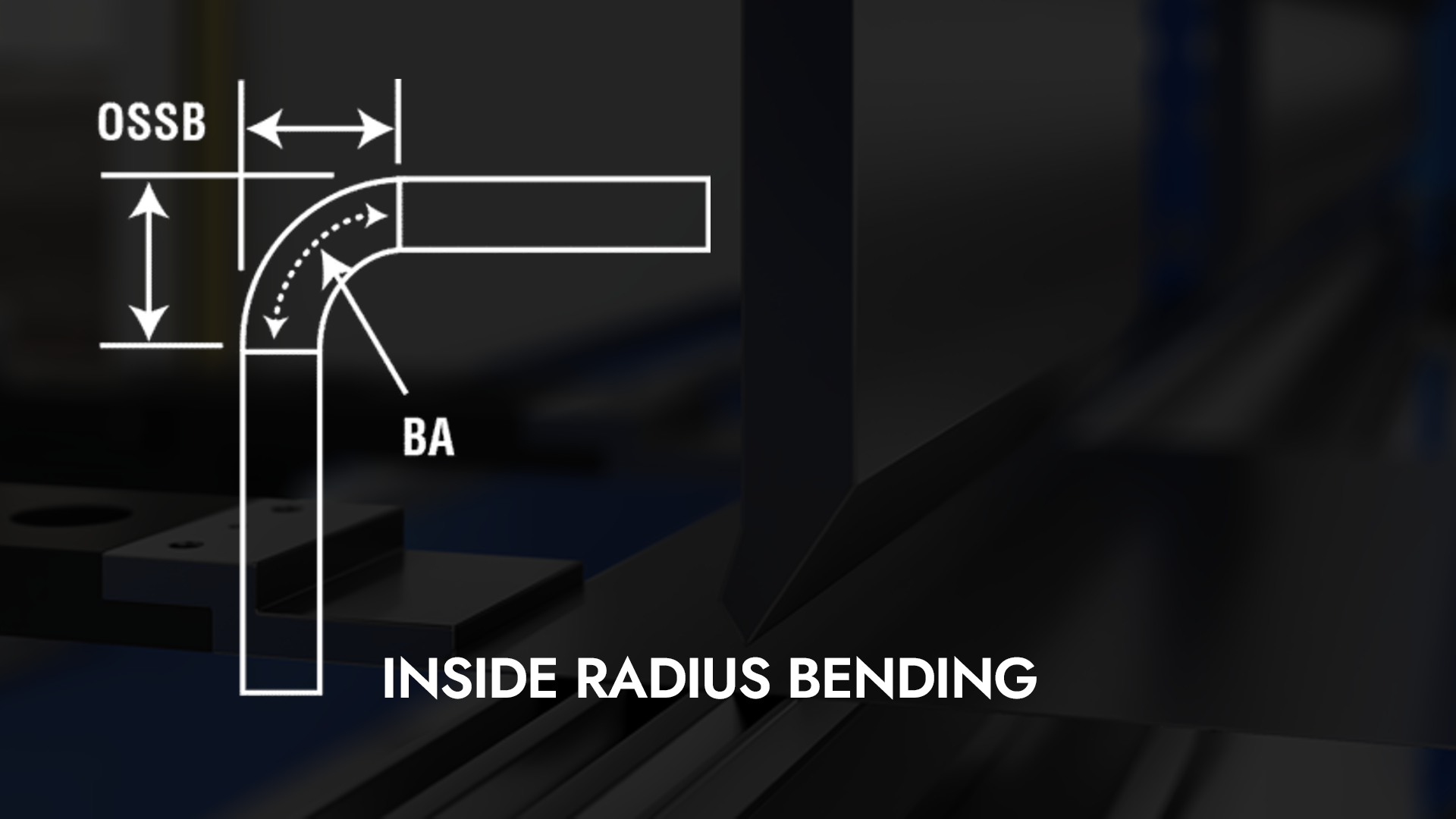
Il cuore di qualsiasi operazione di piegatura è il raggio interno della curva. Se si riesce a calcolare la deduzione di piega in base ai risultati effettivi, la precisione è assicurata. L'unico difetto di questa teoria è che spesso durante la formatura non si forma un raggio reale. La forma che si sta formando può essere una parabola, una curva speculare simmetrica, generalmente a forma di U se orientata come mostrato in Figura 1. E il raggio finale ottenuto è il risultato del ritorno elastico.
- Effetti di ritorno elastico
Come possiamo quindi prevedere la curvatura interna più accurata e la corretta deduzione della curvatura? Per farlo manualmente, la matematica si addentra nei dettagli, quindi non entrerò nei dettagli. Utilizzeremo semplicemente due diversi calcolatori online.
Il primo è su www.harsle.com. Clicca su "The Complete Circular Arc Calculator". Nota che l'etichetta "Larghezza dell'arco" nella calcolatrice corrisponde alla larghezza della matrice, e "Angolo sotteso dall'arco" corrisponde all'angolo di piega incluso.
Assicuratevi che le impostazioni dimensionali della calcolatrice siano corrette per i dati che state utilizzando: pollici, piedi, millimetri, ecc. Notate che quando clicchiamo su Invio, le risposte che otteniamo sono puramente matematiche e non sono state considerate per la resistenza alla trazione del materiale.
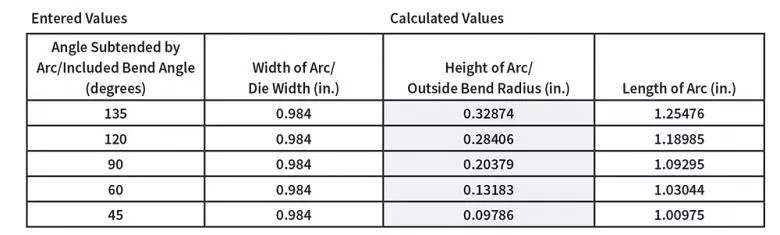
Come mostrato in questo calcolo tratto da The Complete Circular Arc Calculator su www.harsle.com, all'aumentare dell'angolo di piegatura incluso aumenta anche il raggio (altezza dell'arco).
L'informazione che stiamo cercando sulla calcolatrice è l'altezza dell'arco, che equivale al raggio di curvatura esterno. Troviamo un valore per il nostro acciaio di base, laminato a freddo da 60 KSI, spesso 0,125 pollici, utilizzando una matrice di 0,984 pollici di larghezza. Si noti che stiamo parlando di formatura ad aria, quindi l'angolo della matrice non farà differenza; può essere una matrice a canale, a punta o a V. È la larghezza che conta.
Per prima cosa, entriamo nell'angolo rilassato, ovvero i 90 gradi che vogliamo raggiungere.
Valori immessi
Angolo sotteso dall'arco (angolo di piegatura incluso): 90 gradi
Larghezza dell'arco (larghezza della matrice): 0,984 pollici.
Valore calcolato
Altezza dell'arco (raggio di curvatura esterno): 0,20379 pollici.
Questi calcoli, tuttavia, non tengono conto del ritorno elastico. Nel nostro esempio, utilizzeremo un valore di 1 grado per il ritorno elastico, che si verifica quando abbiamo un rapporto approssimativo di 1 a 1 tra lo spessore del materiale e il raggio di piegatura interno. Dopo che il punzone rilascia la pressione di formatura, il materiale torna elastico di 1 grado, quindi per compensare utilizziamo un angolo di piegatura di 89 gradi inclusi. Utilizzando nuovamente il calcolatore completo dell'arco circolare su harsle.com, inseriamo quanto segue:
Valori immessi
Larghezza dell'arco (larghezza della matrice): 0,984 pollici.
Angolo sotteso dall'arco (angolo di piegatura incluso): 89 gradi
Valore calcolato
Altezza dell'arco (raggio di curvatura esterno): 0,201 pollici.
Ora prendiamo il valore dell'altezza dell'arco per il nostro nuovo angolo di piegatura e lo inseriamo nella seguente formula:
Altezza dell'arco – (2 × Spessore del materiale2) = Raggio interno
0,201 – (2 × 0,01562) = Raggio di curvatura interno
0,201 – 0,031 = 0,170 pollici Raggio di curvatura interno
Si noti che questo approccio basato sull'altezza dell'arco è diverso da quello adottato nella rubrica "Nozioni di base sulla piegatura" del mese scorso, quando abbiamo utilizzato la lunghezza dell'arco. Il mese scorso abbiamo calcolato un raggio interno in base alla larghezza dell'apertura della matrice; questa volta utilizziamo un raggio specifico.
Il mese scorso abbiamo calcolato un raggio di 0,136 pollici, e poco fa abbiamo calcolato il raggio interno usando un metodo diverso e siamo arrivati a 0,170 pollici, una differenza di 0,034 pollici. Inoltre, se usassimo la regola del 20% (di nuovo, per l'acciaio laminato a freddo da 60 KSI il raggio è calcolato essere circa il 16% della larghezza della matrice), calcoleremmo un raggio interno di 0,157 pollici, a metà strada tra le due misurazioni precedenti. Questi sono tutti modi diversi per calcolare un raggio, con risultati leggermente diversi. Ma sì, la tana del Bianconiglio si fa più profonda!
- Parabola e curve strette
Se si utilizza un valore del raggio del punzone uguale o inferiore al raggio minimo di piegatura a gomito per la formazione di un pezzo in aria, non si creerà più un raggio nel pezzo (per maggiori informazioni sulle piegature a gomito, si creerà invece una parabola). In effetti si sta tirando una lunghezza di arco diversa nell'apertura dello stampo.
Per prevedere come si formerà questa parabola, possiamo ricorrere a un altro calcolatore online:
Inseriamo il raggio esterno e la larghezza della matrice per trovare la lunghezza dell'arco della parabola. Il valore di Altezza in questo calcolatore online è equivalente al raggio di curvatura esterno, mentre il valore di Larghezza è equivalente alla larghezza della matrice:
Valori immessi
Altezza: (raggio esterno): 0,201 pollici.
Larghezza (larghezza della matrice): 0,984 pollici.
Valore calcolato
Lunghezza dell'arco: 1,0845 pollici.
Qui la profondità della parabola (o altezza dell'arco) è 0,201 pollici e la lunghezza dell'arco della parabola è 1,0845 pollici. Ricordate questi valori. Tornando ora a The Complete Circular Arc Calculator su www.harsle.com, inseriamo la lunghezza dell'arco a 1,0845 pollici e la larghezza della matrice a 0,984 pollici.
Valori immessi
Lunghezza dell'arco: 1,0845 pollici.
Larghezza dell'arco (larghezza della matrice): 0,984 pollici.
Valori calcolati
Altezza dell'arco (raggio di curvatura esterno): 0,195 pollici.
Angolo sotteso dall'arco
(angolo di piegatura incluso): 86,679 gradi
Facendo questo, vedrete che l'altezza dell'arco (ovvero il raggio esterno) è di 0,195 pollici, leggermente inferiore al raggio esterno di 0,201 pollici del calcolatore precedente, che non teneva conto dell'effetto parabola. Sapendo questo, possiamo affermare con sicurezza che il raggio interno diminuisce quando si forma una parabola, il che si verifica quando si utilizza un raggio del punzone inferiore al raggio minimo di piegatura a gomito. Si noti che la parabola richiede anche un angolo di piegatura maggiore per produrre l'angolo di piegatura rilassato desiderato; siamo passati da un angolo di piegatura incluso di 89 a uno di 86,68 gradi, con un ritorno elastico aggiuntivo di 2,32 gradi. Si noti inoltre che il raggio interno del pezzo non sarà inferiore al raggio della punta del punzone.
- Angolo e raggi di curvatura
Ricordate che qualsiasi variazione di raggio comporta una variazione dell'angolo di piega. Se inseriamo la larghezza della matrice e l'angolo di piega incluso su www.harsle.com, otteniamo i risultati mostrati in Figura 2.
I risultati mostrano che quando si forma l'aria, il raggio diminuisce con l'angolo di piegatura incluso (escluse le curve strette).
Questa relazione angolo di piegatura/raggio si interrompe ad angoli inclusi inferiori a 28 gradi inclusi (152 gradi complementari), sebbene l'angolo incluso minimo possa essere maggiore nei materiali con un ritorno elastico significativo.
Ciò è vero in parte perché l'angolo minimo di punzonatura della pressa piegatrice è di 28 gradi inclusi. Detto questo, continuare a chiudere la piega oltre i 28 gradi inclusi comporterà una qualche forma di appiattimento. Il raggio verrà compresso fino al raggiungimento dell'angolo di piega desiderato o al completamento di un'operazione di graffatura. (Come nota a margine, per un orlo chiuso il raggio è zero e la detrazione della piega è calcolata come percentuale dello spessore del materiale: il 43% in condizioni perfette, sebbene sia un'operazione che dipende molto dall'operatore.)
- Fattorizzazione per la resistenza alla trazione
Nell'esempio precedente, abbiamo utilizzato 1 grado di ritorno elastico per effettuare i calcoli. Per l'acciaio dolce laminato a freddo da 60 KSI, il ritorno elastico medio è di 1 grado o meno. E per gli altri materiali?
Per questo, possiamo prevedere lo springback con un ragionevole grado di accuratezza utilizzando la seguente formula, che richiede di convertire tutti i valori in unità di misura metriche. Si noti che la previsione dello springback non è mai accurata al 100%. Tuttavia, queste formule svolgono un ottimo lavoro.
[(Raggio interno in millimetri/2)/
Spessore del materiale in millimetri] × Fattore di trazione
Fattore di trazione = Resistenza alla trazione del materiale in PSI/60.000
Per prima cosa calcoliamo il ritorno elastico come se stessimo lavorando con il nostro materiale di base da 60 KSI con un raggio di curvatura interno di 0,170 pollici:
[(Raggio interno in millimetri/2)/
Spessore del materiale in millimetri] × Fattore di trazione
Spessore del materiale: 0,125 pollici × 25,4 = 3,175 mm
Raggio di curvatura interno: 0,170 pollici × 25,4 = 4,318 mm
(4.318/2) /3.175
2,159 mm /3,175 mm = 0,68 gradi di ritorno elastico
In questo esempio, arrotondiamo questo valore a 1 grado. Possiamo quindi applicare il fattore di trazione per l'acciaio inossidabile 88-KSI 304.
Fattore di trazione = Resistenza alla trazione del materiale in PSI/60.000
88,000/60,000 = 1.466666
1,0 grado × 1,466666
Ciò ci dà 1,46 gradi per l'acciaio inossidabile 88-KSI 304. Arrotondando per eccesso, otteniamo 1,5 gradi di ritorno elastico stimato con un rapporto 1 a 1 tra raggio interno e spessore del materiale.
- Torna alla calcolatrice
Ora che puoi stimare il ritorno elastico con un ragionevole livello di accuratezza, puoi compensarlo. Per determinare l'angolo necessario per compensare il ritorno elastico, è sufficiente sottrarre il valore del ritorno elastico se si lavora con angoli di piega inclusi, oppure aggiungerlo se si utilizzano angoli di piega complementari. Il calcolatore dell'arco circolare su www.harsle.com funziona con gli angoli di piega inclusi (di nuovo, etichettati come Angolo di arco sotteso).
Una volta che si conosce il raggio interno, ovvero il raggio interno effettivo che apparirà nel pezzo finito, è possibile inserire il valore del raggio nelle formule di piegatura (vedere la barra laterale).
Conclusione
Prevedendo correttamente il raggio interno, possiamo calcolare con precisione le deduzioni di curvatura. Tra i diversi modi in cui è possibile prevedere il raggio interno, nessuno è perfetto, ma questo è il migliore possibile. Tuttavia, la curvatura ha troppe variabili per raggiungere una precisione del 100%.
Anche nella formatura ad aria compressa è fondamentale che l'ingegnere o il programmatore informi il tecnico sui set di utensili con cui è stata progettata ogni piega. Inoltre, il tecnico deve comprendere l'importanza fondamentale dell'utilizzo di tali utensili per ottenere pezzi di qualità.
Il mese prossimo parleremo di come calcolare il raggio interno delle curve in cui il rapporto tra raggio interno e spessore del materiale diventa molto elevato: le curve a raggio profondo. Le curve a raggio ampio presentano problemi con l'angolo e la larghezza della matrice, la rottura multipla e, naturalmente, un ritorno elastico molto elevato.
La tana del Bianconiglio ha ancora molta strada da fare, ma ne vale sicuramente la pena.
Una revisione delle formule di flessione
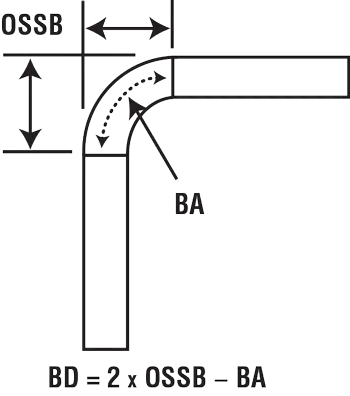
Queste formule per la tolleranza di piegatura, l'arretramento esterno e la deduzione di piegatura sono ben consolidate e ogni valore può essere utilizzato in modi diversi per calcolare il layout del pezzo piatto.
Formule
BA = [(0,017453 × Rp) + (0,0078 × Mt)]
× Gradi di curvatura complementari
OSSB = [Tangente (grado dell'angolo di piega/2)]
× (Mt + Rp)
BD = (OSSB × 2) – BA
Chiave
Rp = Raggio del naso del punzone (fondo)
o il raggio interno flottante (formazione di aria)
Mt = Spessore del materiale
BA = Tolleranza di piegatura
BD = Deduzione di piega
OSSB = Arretramento esterno
0,017453 = π/180
0,0078 = fattore K × π /180
Fattore K = 0,446











America-Customer-Feedback-1.jpg)
America-Miami-Customer-Feeback-1.jpg)
Uzbekistan-Customer-Feedback1.png)
Kosovo-Customer-Feedback11.png)
Russia-Customer-Feedback.jpg)
Russia-Customer-Feedback-3.jpg)




