Obliczenie prawidłowego układu wzoru płaskiego jest kluczowe dla uzyskania dobrej jakości gotowego elementu. prasa krawędziowaJednak wielu programistów CAD i CNC nie ma pojęcia, jak obliczyć wymagane wartości. Lata temu prawdziwi eksperci tworzyli ściągi i wieszali je na ścianie. Uczyli nowego aplikanta jedynie, jak stosować wyniki przedstawione na ściągach, a nie jak obliczać liczby. Cóż, teraz ci eksperci przeszli na emeryturę i nadszedł czas, aby nowe pokolenie nauczyło się prawidłowo obliczać układ płaskiego wzoru. Możesz również skorzystać z naszych kalkulator naddatku na zginanie Lub kalkulator odliczeń od zginania aby łatwo uzyskać wyniki.

Obliczenie długości płaskiego wzoru z części 3D naprawdę nie jest takie trudne. Chociaż można znaleźć kilka różnych wzorów, które twierdzą, że… obliczyć Naddatek na zginanie (patrz Definicje gięcia) – zazwyczaj jest to ten sam wzór, uproszczony jedynie poprzez podanie kąta lub współczynnika K. Aha, i tak, musisz znać współczynnik K, aby obliczyć naddatek na zginanie.

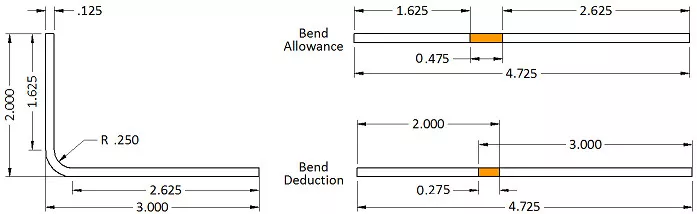
Weźmy na przykład prosty wspornik kątowy. Ma on dwie nogi, jedną o długości 2 cali, a drugą 3 cali, grubość materiału 0,125 cala i wewnętrzny promień gięcia 0,250 cala. Kąt gięcia wynosi 90 stopni. Aby obliczyć długość płaską, nie mierzy się jej od powierzchni wewnętrznej ani zewnętrznej, lecz od osi neutralnej. W tym przypadku wykorzystywany jest współczynnik K. Współczynnik K reprezentuje położenie osi neutralnej jako procent grubości materiału. Do tego obliczenia użyjemy współczynnika K równego 0,42, aby określić prawidłowy naddatek na zagięcie i wzór płaskiego przekroju.

Wzór (patrz Wzory na zginanie) jest następujący: 

Dodatek na zgięcie = Kąt * (π / 180) * (Promień + współczynnik K * Grubość). 

Podstawiając nasze liczby, otrzymujemy: Naddatek na zgięcie = 90 * (π / 180) * (0,250 + 0,42 * 0,125) = 0,475″

Długość płaskiego wzoru wynosi zatem 1,625” + 2,625” + 0,475″, co daje 4,725″. Jeśli zsumujesz płaską długość wszystkich kołnierzy i dodasz jeden naddatek na zgięcie dla każdego obszaru zgięcia, otrzymasz prawidłową płaską długość elementu.

Przyjrzyjmy się teraz bliżej rysunkowi. W rzeczywistym projektowaniu blach, wymiary są zazwyczaj podawane do przecięcia kołnierzy – jest to znane jako linia formy. Z tego powodu należy odjąć od sumy dwukrotność grubości materiału plus promień gięcia, aby uwzględnić każdy obszar gięcia. Wartość ta nazywa się odsunięciem. W takich przypadkach użycie kompensacji gięcia jest często prostsze. Kompensacja gięcia pozwala na użycie wymiarów linii formy dla każdego kołnierza, a następnie skorygowanie sumy poprzez dodanie jednej wartości kompensacji na każde gięcie. W tym przypadku kompensacja wynosi -0,275, więc 5 cali po odjęciu staje się 4,725 cala.

Definicje:

Dodatek na zgięcie = Kąt * (π / 180) * (Promień + współczynnik K * Grubość) 

Kompensacja zagięcia = Dodatek na zagięcie – (2 * Odsunięcie)

Odsunięcie wewnętrzne = tan (kąt / 2) * promień zewnętrzny 

Odsunięcie = tan (kąt / 2) * (promień + grubość)

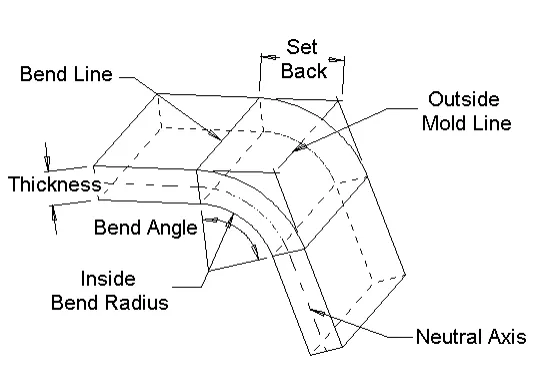
Naddatek na zginanie – Długość łuku przechodzącego przez obszar zagięcia w osi neutralnej.

Kąt zgięcia – Kąt zawarty między łukiem a podstawą powstały w wyniku gięcia.

Kompensacja zgięcia – Wartość, o jaką materiał jest rozciągany lub ściskany w procesie gięcia. Zakłada się, że wszelkie rozciąganie lub ściskanie ma miejsce w obszarze gięcia.

Linie zagięcia – Proste linie na wewnętrznej i zewnętrznej powierzchni materiału, w miejscu, gdzie granica kołnierza styka się z obszarem gięcia.

Wewnętrzny promień gięcia – Promień łuku na wewnętrznej powierzchni obszaru gięcia.

Współczynnik K – Określa położenie osi neutralnej. Jest ona mierzona jako odległość od wewnętrznej strony materiału do osi neutralnej podzielona przez grubość materiału.

Linie form – W przypadku gięcia o kącie mniejszym niż 180 stopni, linie formy to linie proste, w których przecinają się powierzchnie kołnierza ograniczające obszar gięcia. Dzieje się tak zarówno na wewnętrznej, jak i zewnętrznej powierzchni gięcia.

Oś neutralna – Patrząc na przekrój poprzeczny zagięcia, oś obojętna to teoretyczne miejsce, w którym materiał nie jest ani ściskany, ani rozciągany.

Cofać – W przypadku gięcia pod kątem mniejszym niż 180 stopni, odsunięcie jest odległością od linii gięcia do linii formy.

Jak obliczyć współczynnik „K”:

O ile mi wiadomo, nie ma wzoru na obliczenie współczynnika k. Jestem pewien, że gdzieś jakiś inżynier matematyk ma wzór. Ale jest on prawdopodobnie zbyt skomplikowany, by większość z nas mogła go zrozumieć lub wykorzystać.

Współczynnik k to procent grubości materiału, przy którym nie występuje rozciąganie ani ściskanie materiału w obszarze gięcia. Zatem oś neutralna!

Im twardszy materiał, tym mniejsze jest ściskanie po wewnętrznej stronie zagięcia. W związku z tym, większe jest rozciąganie po stronie zewnętrznej, a oś neutralna przesuwa się do wewnątrz zagięcia. Miększe materiały pozwalają na większe ściskanie po stronie wewnętrznej, a oś neutralna pozostaje bliżej środka grubości materiału.

Promień gięcia ma podobny efekt. Im mniejszy promień gięcia, tym większa potrzeba ściskania, a oś neutralna przesuwa się do wewnątrz gięcia. Przy większym promieniu oś neutralna pozostaje w pobliżu środka grubości materiału.

Ogólne współczynniki K	Aluminium		Stal
Promień	Miękkie materiały	Materiały średnie	Materiały twarde
Gięcie powietrza
od 0 do grubości	0.33	0.38	0.40
Grubość do 3×grubości	0.40	0.43	0.45
Grubość większa niż 3×	0.50	0.50	0.50
Dotarcie do dna
od 0 do grubości	0.42	0.44	0.46
Grubość do 3×grubości	0.46	0.47	0.48
Grubość większa niż 3×	0.50	0.50	0.50
Wybijanie monet
od 0 do grubości	0.38	0.41	0.44
Grubość do 3×grubości	0.44	0.46	0.47
Grubość większa niż 3×	0.50	0.50	0.50

Zamiast tabeli można zastosować poniższy wzór, który będzie dobrym przybliżeniem współczynnika K dla zginania powietrza:

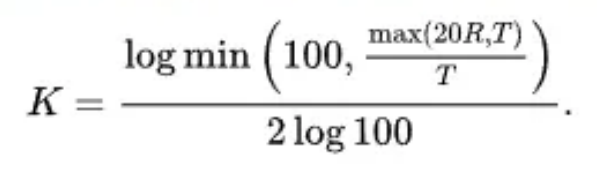
Diagram i wzory obliczeniowe dla naddatku na zginanie

Aby ułatwić i przyspieszyć naukę wzoru na długość gięcia po rozłożeniu, przygotowaliśmy cztery popularne tabele współczynników, zilustrowaliśmy szesnaście wzorów na długość gięcia po rozłożeniu oraz przedstawiliśmy kilka przykładów dla lepszego zrozumienia. Mamy nadzieję, że poniższe informacje okażą się pomocne w praktyce. W razie pytań prosimy o kontakt.

Szerokość rowka V\grubość płyty	0.6	0.8	1.0	1.2	1.5	2.0	2.5	3.0	3.5	4.0	4.5	5.0	Najkrótszy rozmiar
Wersja 4	0.9	1.4											2.8
Wersja 6		1.5	1.7	2.0									4.5
Wersja 7			1.8	2.1	2.4								5.0
V8			1.9	2.2	2.5								5.5
Wersja 10			2.1	2.3	2.7								7.0
Wersja 12			2.2	2.5	2.8	3.4							8.5
Wersja 14						3.5	3.8			6.4	6.8		10.0
Wersja 16					3.1	3.8	4.5	5.0					11.0
Wersja 18					3.3	4.0							13.0
Wersja 20						4.0	4.9	5.1		6.6	7.2	7.8	14.0
V25						4.4	5.0	5.5		6.8	7.8	8.3	16.5
Wersja 32						5.0	5.5	6.1		8.7

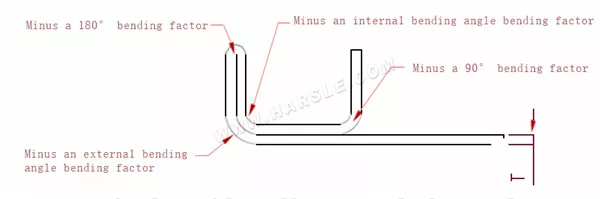
Notatka: Jeśli rozmiar graficzny części jest oznaczony tolerancją ujemną, wartość współczynnika gięcia można zwiększyć, jak pokazano w tabeli. Czerwona część może zostać zwiększona do: 2,8; 2,82; 3,4; 3,43 lub 3,44: 4,5; 4,6; 5,5: 5,6

Grubość mm\kąt	Rowek formy szerokość		90°	Wewnętrzny róg	Zewnętrzny róg		180°
1.5	Wersja 10		3.0	3.2	4.1		0.8
2.0	Wersja 12		3.8	3.7	4.6		1.0
2.5	Wersja 16		4.5	4.8	6.1		1.3

Grubość  mm\kąt	30°		45°		60°			120°			135°			145°
1.0	0.35		0.7		1.1			1.0			0.6			0.4
1.2	0.4		0.8		1.2			1.0			0.6			0.4
1.5	0.5		1.0		1.6			1.4			0.9			0.6
2.0	0.6		1.2		2.0			1.7			1.1			0.7
2.5	0.8		1.6		2.6			2.2			1.4			0.85
3.0	1.0		2.2		3.4			2.8			2.0			1.2
4.0								3.7			2.4			1.4

Grubość mm		0.5	1.0	1.2		1.5	2.0		2.5	3.0		4.0	5.0		6.0
Otwór procesowy mm		1.Brak dziur 2.Można otworzyć otwór φ2		φ2		φ2,5	φ3,0		φ3,5	φ4,0		φ5,5	φ6,0		φ7,0

Notatka: Jeśli istnieją szczególne potrzeby, można zastosować większy stopień przysłony.

Schemat i wzór obliczeniowy dla jednego zakrętu

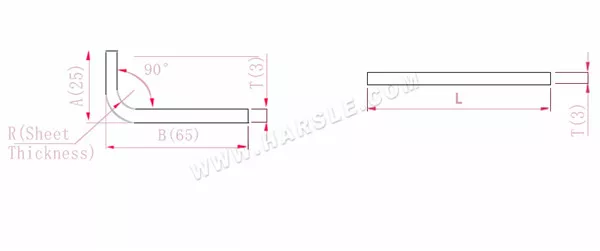
A, B— długość gięcia przedmiotu obrabianego

P'—współczynnik gięcia krawędziowego (współczynnik gięcia: jeden współczynnik minus jedno zgięcie)

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość po rozciągnięciu L=A+B-P', która wynosi L=25+65-5,5=84,5

Zgodnie z tabelą 1 grubość płyty wynosi 3, dolna matryca to V25, a współczynnik gięcia wynosi 5,5

Uwaga: Zgodnie z tabelą 1, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Schemat i wzór obliczeniowy dla dwuzgięciowego

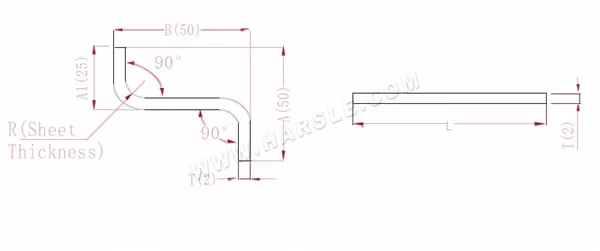
A(A1), B— długość gięcia przedmiotu obrabianego

P'—współczynnik gięcia krawędziowego (współczynnik gięcia: jeden współczynnik minus jedno zgięcie)

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość po rozciągnięciu L=A+T+B-2*P', która wynosi L=50+2+50-2*3,4=95,2

Zgodnie z tabelą 1 grubość płyty wynosi 2, dolna matryca to V12, a współczynnik gięcia wynosi 3,4

Uwaga: Zgodnie z tabelą 1, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Schemat i wzór obliczeniowy trójfazowego

A(A1), B (B1) – długość gięcia przedmiotu obrabianego

P'—współczynnik gięcia krawędziowego (współczynnik gięcia: jeden współczynnik minus jedno zgięcie)

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość po rozciągnięciu L=A+T+B+T-3*P', która wynosi L=50+2+90+2-3*3,4=133,8

Zgodnie z tabelą 1 grubość płyty wynosi 2, dolna matryca to V12, a współczynnik gięcia wynosi 3,4

Uwaga: Zgodnie z tabelą 1, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Schemat i wzór obliczeniowy dla czterokątów 

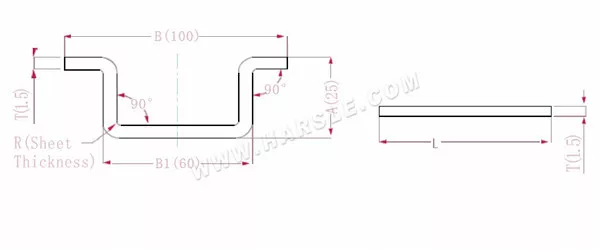
A, B (B1) – długość gięcia przedmiotu obrabianego

P'—współczynnik gięcia krawędziowego (współczynnik gięcia: jeden współczynnik minus jedno zgięcie)

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość po rozciągnięciu L=A+A+B+T+T-4*P', która wynosi l = 25+25+100+1,5+1,5-4 * 2,8 = 141,8

Zgodnie z tabelą 1 grubość płyty wynosi 1,5, dolna matryca to V12, a współczynnik gięcia wynosi 2,8

Uwaga: Zgodnie z tabelą 1, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Schemat i wzór obliczeniowy dla sześciozgięciowego 

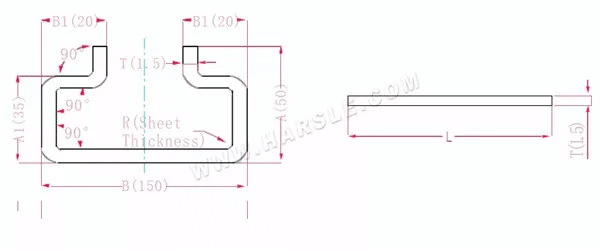
A(A1), B (B1) – długość gięcia przedmiotu obrabianego

P'—współczynnik gięcia krawędziowego (współczynnik gięcia: jeden współczynnik minus jedno zgięcie)

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość po rozszerzeniu L=A+T+A+T+B+B1+B1-6*P'

co wynosi l = 50+1,5+50+1,5+150+20+20-6 * 2,8 = 276,2

Zgodnie z tabelą 1 grubość płyty wynosi 1,5, dolna matryca to V12, a współczynnik gięcia wynosi 2,8

Uwaga: Zgodnie z tabelą 1, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Schemat i wzór obliczeniowy gięcia o 180 stopni

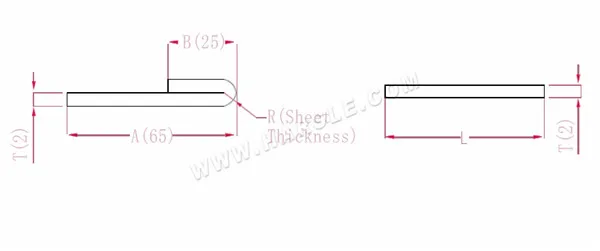
A, B— długość gięcia przedmiotu obrabianego

P'—współczynnik gięcia wyokrąglenia spłaszczającego

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość po rozciągnięciu L=A+B-P', która wynosi L=25+65-1=89

Zgodnie z tabelą 2 grubość płyty wynosi 2, dolna matryca to V12, a współczynnik gięcia wynosi połowę grubości płyty

Uwaga: Zgodnie z Tabelą 2, wybór różnych dolnych matryc wiąże się z różnymi współczynnikami gięcia i różnymi grubościami płyt.

Schemat i wzór obliczeniowy gięcia dwuwarstwowego 

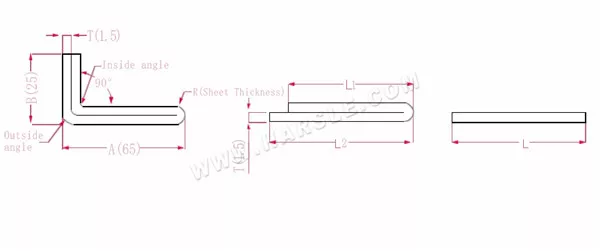
A, B— długość gięcia przedmiotu obrabianego

P1— współczynnik ugięcia narożnika wewnętrznego

P2— współczynnik zgięcia zewnętrznego kąta zgięcia

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość po rozszerzeniu L1=(A-1,5) +(B-1,5)-P1, czyli L1= (65-1,5) +(25-1,5)-3,2=83,8

L2=A+B-P2, czyli L2=65+25-4,1=85,9

L=L1+L2-T/2, czyli L=83,8+85,9-0,75=168,95

Zgodnie z tabelą 2 grubość płyty wynosi 1,5, dolna matryca to V12, współczynnik gięcia naroża wewnętrznego wynosi 3,2, współczynnik gięcia naroża zewnętrznego wynosi 4,1, a współczynnik gięcia 180° wynosi 0,75.

Uwaga: Zgodnie z tabelą 2, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Schemat i wzór obliczeniowy gięcia dwuwarstwowego z jedną krawędzią

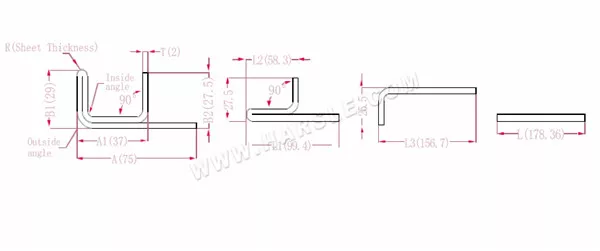
A, A1, A2, B1, B2, L, L1, L2, L3 — długość gięcia przedmiotu obrabianego

P1— współczynnik ugięcia narożnika wewnętrznego

P2— współczynnik zgięcia zewnętrznego kąta zgięcia

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość po rozszerzeniu L1=(A1-T) +(B2-T)-P1, która wynosi L1= (35-2) +(34-2)-3,7=61,3

L2=(B1-T) +(A2-T)-P1, czyli L2= (50-2) +(34-2)-3,7=76,3

L3=A+B1+B2-2*P2, czyli L3=70+35+50-2*4,6+145,8

L=L1+L2+L3-2*P3, czyli L=61,3+75,3+145,8-2*1=280,4

Zgodnie z tabelą 2 grubość płyty wynosi 2, dolna matryca to V12, współczynnik gięcia naroży wewnętrznych wynosi 3,7, współczynnik gięcia naroży zewnętrznych wynosi 4,6, a współczynnik gięcia pod kątem 90° wynosi 1.

Uwaga: Zgodnie z tabelą 2, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Schemat i wzór obliczeniowy gięcia dwuwarstwowego z dwiema krawędziami

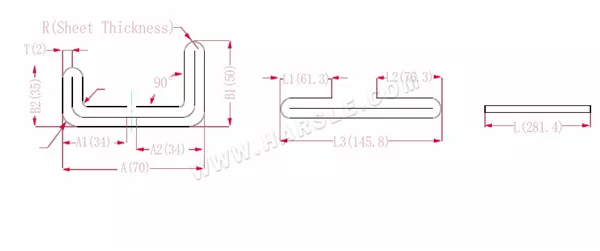
A, A1, A2, B1, B2, L, L1, L2, L3 — długość gięcia przedmiotu obrabianego

P1— współczynnik ugięcia narożnika wewnętrznego

P2— współczynnik zgięcia zewnętrznego kąta zgięcia

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość po rozszerzeniu L1=(A1-T) +(B2-T)-P1, która wynosi L1= (35-2) +(34-2)-3,7=61,3

L2=(B1-T) +(A2-T)-P1, czyli L2= (50-2) +(34-2)-3,7=76,3

L3=A+B1+B2-2*P2, czyli L3=70+35+50-2*4,6+145,8

L=L1+L2+L3-2*P3, czyli L=61,3+75,3+145,8-2*1=280,4

Zgodnie z tabelą 2 grubość płyty wynosi 2, dolna matryca to V12, współczynnik gięcia naroży wewnętrznych wynosi 3,7, współczynnik gięcia naroży zewnętrznych wynosi 4,6, a współczynnik gięcia pod kątem 90° wynosi 1.

Uwaga: Zgodnie z tabelą 2, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Schemat i wzór obliczeniowy gięcia schodkowego

A, B— długość gięcia przedmiotu obrabianego

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość po rozłożeniu L=A+1

Uwaga: Jeżeli grubość stopnia jest równa grubości dwóch płyt, należy dodać 0,5 dla każdego stopnia i 1 dla każdego stopnia.

Schemat i wzór obliczeniowy kąta specjalnego gięcia 1

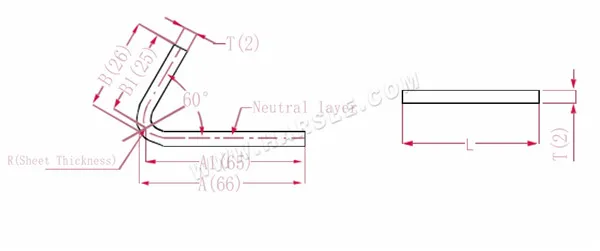
A(A1), B (B1) – długość gięcia przedmiotu obrabianego

P'—współczynnik gięcia krawędziowego (współczynnik gięcia: jeden współczynnik minus jedno zgięcie)

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość rozszerzenia L=(AT) +(BT)-P', która wynosi L= (66-1) +(26-1)-2=65+25-2=88

Zgodnie z tabelą 3 grubość blachy wynosi 2, dolna matryca to V12, a współczynnik gięcia 60 wynosi 2

Uwaga: Zgodnie z tabelą 3, warstwa neutralna jest wybierana jako długość i szerokość gięcia.

Schemat i wzór obliczeniowy kąta specjalnego gięcia 2

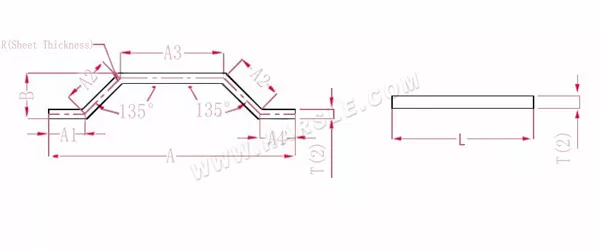
A (A1, A2, A3, A4), B — długość gięcia przedmiotu obrabianego

P— współczynnik gięcia 135 kątów gięcia

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Długość po rozszerzeniu L = A1+A2+A3+A2+A4-PP.

Uwaga: ten sam krok gięcia ciśnienia wymaga jedynie zmniejszenia dwóch współczynników

Zgodnie z tabelą 3: grubość płyty wynosi 2, dolna matryca to V12, a współczynnik gięcia przy 135 wynosi 1,1.

Schemat i wzór obliczeniowy kąta specjalnego gięcia 3

A (A1, A2), B (B1, B2) – długość gięcia przedmiotu obrabianego

P1—współczynnik gięcia 120°

P2—współczynnik zgięcia 145°

P3—współczynnik gięcia 90°

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

Uwaga: jeśli na kształcie zaznaczony jest rozmiar grafiki, wówczas podczas obliczania długości rozwinięcia należy przeliczyć rozmiar kształtu na rozmiar warstwy neutralnej;

Długość po rozszerzeniu L=A11+B11+B21+A21-P1-P2-P3, która wynosi l = 80+50+103+70-1,7-0,7-3,4 = 297,2

Zgodnie z tabelą 3: grubość płyty wynosi 2, dolna matryca to V12, współczynnik gięcia 120 wynosi 1,7, współczynnik gięcia 145 wynosi 0,7, a współczynnik gięcia 90 wynosi 3,4

Uwaga: Zgodnie z tabelą 3, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Schemat i wzór obliczeniowy wiązania wspólnego 1

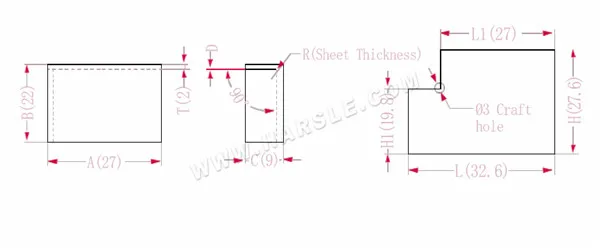
A, B, C — długość, szerokość i wysokość krawędzi gięcia przedmiotu obrabianego

P— współczynnik zginania

R—gięcie i wyokrąglenie (zwykle grubość blachy)

H(H1), l (L1) – rozłożona długość każdego boku

T— grubość materiału

D— luz w procesie gięcia (zwykle 0~0,5)

Długość po rozszerzeniu L1=A, która wynosi L1=27

L=A+CP, czyli L=27+9-3,4=32,6

H1=BTD, czyli H1=22-2-0,2=19,8. Uwaga: D wynosi 0,2.

H=B+CP, czyli H=22+9-3,4=27,6

Zgodnie z tabelą 1: grubość blachy wynosi 2, dolna matryca to V12, a współczynnik gięcia wynosi 3,4

Uwaga: Zgodnie z tabelą 1, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Schemat i wzór obliczeniowy wiązania wspólnego 2

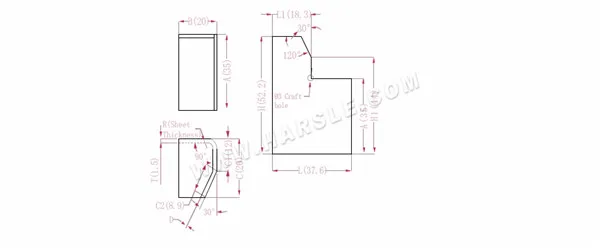
A, B, C — długość, szerokość i wysokość krawędzi gięcia przedmiotu obrabianego

H(H1), L(L1) – rozłożona długość każdego boku

P—współczynnik gięcia 90° P1—współczynnik gięcia 30°

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

D— luz w procesie gięcia (zwykle 0~0,5)

Długość po rozszerzeniu L1=BTD, czyli L1=20-1,5-0,2=18,3

L=B+C1+C2-P-P1, czyli L=20+12+8,9-2,8-0,5=37,6

H1=C1+APD, czyli H1=12+35-2,8-0,2=44. Uwaga: D wynosi 0,2.

H=A+CP, czyli H=35+20-2,8=52,2

Zgodnie z tabelą 1: grubość blachy wynosi 1,5, dolna matryca to V12, współczynnik gięcia wynosi 2,8, a współczynnik gięcia 30 wynosi 0,5

Uwaga: Zgodnie z tabelą 1, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Schemat i wzór obliczeniowy wiązania wspólnego 3

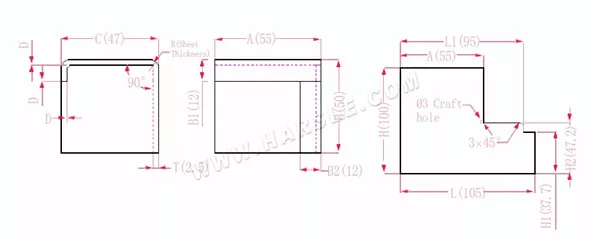
A, B, C — długość, szerokość i wysokość krawędzi gięcia przedmiotu obrabianego

H(H1), L(L1) – rozłożona długość każdego boku

P— współczynnik zginania

R—gięcie i wyokrąglenie (zwykle grubość blachy)

T— grubość materiału

D— luz w procesie gięcia (zwykle 0~0,5)

Długość po rozszerzeniu H1=B-B1-D, czyli H1=50-12-0,3=37,7. Uwaga: D wynosi 0,2.

H2=BTD, czyli H2=50-2,5-0,3=47,2

H=B+C+B1-2*P, czyli H=50+47+12-2*4,5=100

L1=A+CTDP, czyli L1=55+47-2,5-0,3-4,5=94,7

L=A+C+B2-2*P, czyli L=55+47+12-2*4,5=105

Zgodnie z tabelą 1: grubość blachy wynosi 1,5, dolna matryca to V16, a współczynnik gięcia wynosi 4,5

Uwaga: Zgodnie z tabelą 1, różne współczynniki gięcia dla dolnych matryc i różnych grubości płyt są różne.

Demo wideo