Jak obliczyć długość gięcia rowkowego po rozłożeniu?
Z mojego doświadczenia wynika, że pracuję z gięcie rowkoweObliczenie długości po rozłożeniu jest niezbędne do uzyskania dokładnych i precyzyjnych rezultatów w obróbce metalu. Długość po rozłożeniu określa, ile materiału potrzeba przed gięciem, a prawidłowe obliczenie jest kluczowe dla uniknięcia strat i zapewnienia prawidłowego dopasowania. Przez lata wypracowałem systematyczne podejście do obliczania długości po rozłożeniu. długość po rozłożeniu gięcia rowkowego, uwzględniając takie czynniki jak promień gięcia i grubość materiału. W tym artykule podzielę się swoimi spostrzeżeniami na temat obliczania długości gięcia rowkowego po rozwinięciu, podając praktyczne wskazówki, które mogą zwiększyć dokładność gięcia w różnych zastosowaniach.
Zrozumienie gięcia rowkowego
Zanim przejdziemy do obliczeń, ważne jest zrozumienie, na czym polega gięcie rowkowe. Proces ten polega na utworzeniu rowka wzdłuż materiału, aby ułatwić gięcie pod określonym kątem. Rowek zazwyczaj pomaga kontrolować gięcie i zapewnia czystsze, bardziej precyzyjne gięcie. Jednak, aby uzyskać pożądany kąt i kształt, należy znać prawidłową długość materiału po rozłożeniu.
Wzór na rozłożoną długość
Jak pokazano na rysunku, struganie jest teraz używane do gięcia rury kwadratowej o wymiarach 20×20 i grubości blachy wynoszącej 1 mm.
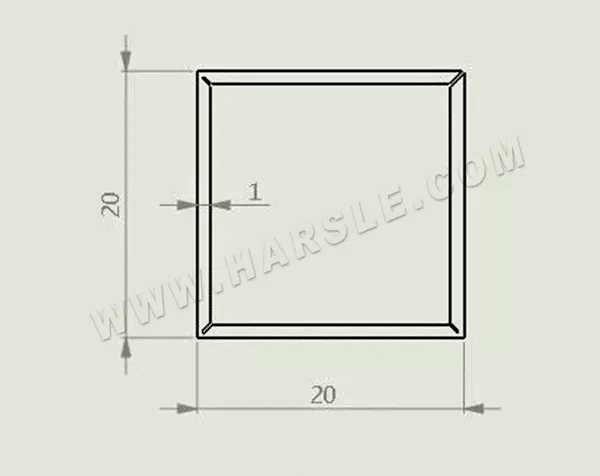
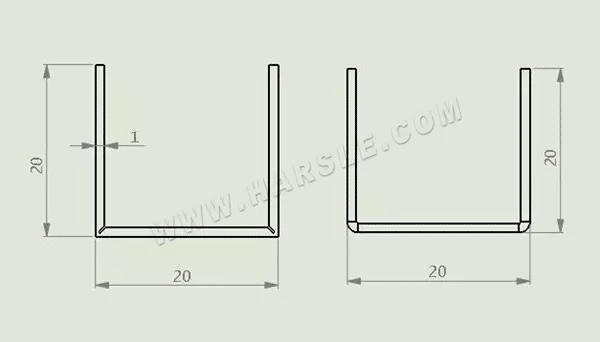
Pozostała grubość materiału a rowka strugania jest związana z rozmiarem łuku prostego po gięciu przez klienta, a także z grubością materiału t. Ogólnie rzecz biorąc, gdy grubość materiału jest mniejsza lub równa 1 mm, a = 0,4 mm, a gdy grubość materiału jest większa niż 1 mm, a = t/2.
L=2×(L1+L2)=2x((długość boku-1xa-0,2)+(długość boku-2xa)) zilustrowanego przykładu
=2x((20-1×0,4-0,2)+(20-2×0,4))=77,2 mm
Uwaga: Jeden koniec L1 jest strugany, bez względu na grubość materiału, odejmuje się 0,2 mm
Porównajmy różnicę pomiędzy obliczeniami gięcia i rozwijania poprzez gięcie szczelinowe i bez szczelinowe:

W przypadku łuków szczelinowych metoda obliczania całkowitej długości jest następująca:
L=20-0,4+20-2X0,4+20-0,4=58,4
W przypadku łuków bez szczelin, metoda obliczania całkowitej długości jest następująca:
●L=(20-1xt+k)+(20-2xt+2xk)+(20-1xt+1xk)=(20-1+0,2)+(20-2+2×0,2)+(20-1+ 0,2)=56,8 mm
●t to grubość materiału, k to współczynnik, którego wartość k jest związana z grubością materiału i zwykle wynosi od 0,2 do 0,25. Im grubszy materiał, tym większa wartość K. W tym przykładzie k wynosi 0,2.
Poniżej przedstawiono kombinację szczeliny w kształcie litery Z i jej braku, służącą do obliczenia długości rozłożonego gięcia:
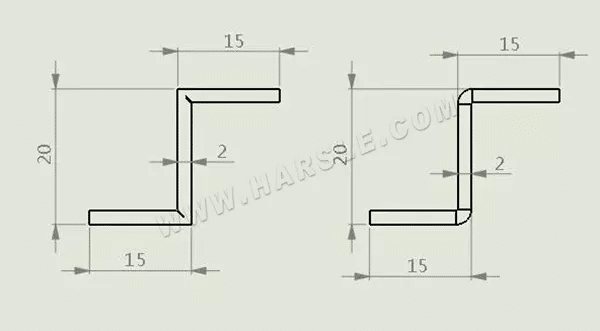
W przypadku płyty o grubości 2 mm pozostałą grubość materiału a rowka strugania przyjmuje się jako t/2=1 mm (jeśli klient wymaga mniejszego łuku bezpośredniego, należy wybrać wartość a mniejszą niż 1 mm). Tak więc długość rozszerzenia:
Długość = 15-1 + 20-2 × 1 + 15-1 = 46 mm
Dla płyty o grubości 2 mm, bez rowkowania i gięcia, współczynnik k przyjmuje się na poziomie 0,25, więc długość po rozłożeniu wynosi:
L=(15-2+0,25)+(20-2×2+2×0,25)+(15-2+0,25)=43mm
Poniżej opisano metodę obliczeniową na przykładzie rowkowania i nierowkowania przedmiotu obrabianego wielogiętego:

W przypadku płyty o grubości 3 mm przyjmuje się, że klient wymaga mniejszego łuku prostego, wówczas pozostała grubość materiału wynosi 0,5 mm, a długość po rozciągnięciu L=(40-0,5)+(30-2×0,5)+(30-2×0,5) +(10-0,5)=107 mm;
Dla płyty o grubości 3 mm współczynnik k przyjmuje wartość 0,25, więc długość po rozłożeniu wynosi:
L=(40-3+0,25)+(30-6+2×0,25)+(30-6+2×0,25)+(10-3+0,25)=93,5mm
Poniżej przedstawiono przykład gięcia odwrotnego po rowkowaniu, mający na celu wprowadzenie do metody obliczania rozszerzalności:
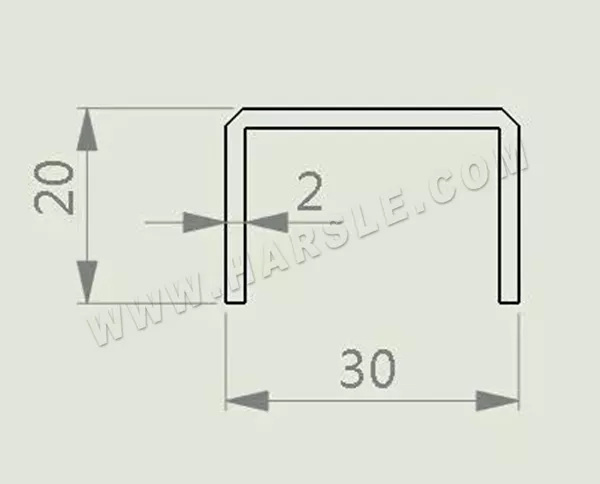
Do wygięć pleców po wyżłobieniu, jak pokazano
Oblicz długość rozszerzenia jako
Długość = (20-2+0,2) + (30-2×2+2×0,2) + (20-2+0,2) = 62,8 mm









