Die Berechnung des richtigen Flachmuster-Layouts ist entscheidend, um ein qualitativ hochwertiges Fertigteil von Ihrem Abkantpresse. Dennoch haben viele CAD- und CNC-Programmierer keine Ahnung, wie sie die erforderlichen Werte berechnen sollen. Früher haben die echten Experten Spickzettel erstellt und an die Wand geheftet. Sie haben dem neuen Lehrling nur beigebracht, wie man die auf dem Spickzettel gezeigten Ergebnisse anwendet, nicht, wie man die Zahlen berechnet. Nun sind diese Experten in Rente gegangen, und es ist Zeit für eine neue Generation, die richtige Berechnung des richtigen Abwicklungslayouts zu erlernen. Sie können auch unsere Biegezugaberechner oder Biegeabzugsrechner um die Ergebnisse einfach zu erhalten.

Die Berechnung der Abwicklungslänge aus dem 3D-Teil ist wirklich nicht so schwierig. Obwohl Sie verschiedene Formeln finden, die behaupten, berechnen Sie die Biegezugabe (siehe Biegedefinitionen). Normalerweise handelt es sich um dieselbe Formel, die nur durch das Einfügen des Winkels oder eines K-Faktors vereinfacht wird. Ach ja, und ja, Sie müssen den K-Faktor kennen, um die Biegezugabe zu berechnen.

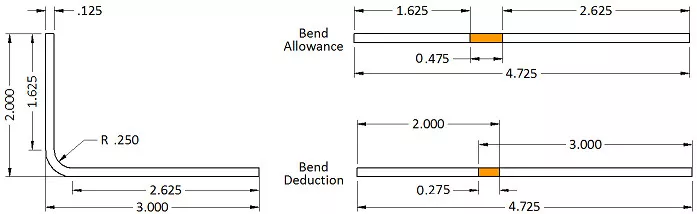
Nehmen wir als Beispiel eine einfache L-Klammer. Sie hat zwei Schenkel, einen 2 Zoll und einen 3 Zoll langen, mit einer Materialstärke von 0,125 Zoll und einem inneren Biegeradius von 0,250 Zoll. Der Biegewinkel beträgt 90 Grad. Um die flache Länge zu bestimmen, messen Sie nicht von der Innen- oder Außenfläche, sondern berücksichtigen die neutrale Achse. Hier kommt der K-Faktor zum Einsatz. Der K-Faktor gibt die Position der neutralen Achse als Prozentsatz der Materialstärke an. Für diese Berechnung verwenden wir einen K-Faktor von 0,42, um die richtige Biegezugabe und das richtige flache Muster zu bestimmen.

Die Formel (siehe Biegeformeln) lautet: 

Biegezugabe = Winkel * (π / 180) * (Radius + K-Faktor * Dicke). 

Wenn wir unsere Zahlen einsetzen, erhalten wir: Biegezugabe = 90 * (π / 180) * (0,250 + 0,42 * 0,125) = 0,475″

Die Länge des Abwicklungsmusters beträgt also 1,625" + 2,625" + 0,475", was 4,725" entspricht. Wenn Sie also die Abwicklungslänge aller Flansche addieren und für jeden Biegebereich eine Biegezugabe hinzufügen, erhalten Sie die richtige Abwicklungslänge des Teils.

Sehen Sie sich nun die Zeichnung genauer an. In der realen Blechkonstruktion werden die Abmessungen üblicherweise bis zum Schnittpunkt der Flansche angegeben – dies wird als Formlinie bezeichnet. Aus diesem Grund müssen Sie vom Gesamtwert die doppelte Materialstärke plus den Biegeradius abziehen, um jeden Biegebereich zu berücksichtigen. Dieser Wert wird als Rücksprung bezeichnet. In solchen Fällen ist die Verwendung der Biegekompensation oft einfacher. Mit der Biegekompensation können Sie für jeden Flansch Formlinienabmessungen verwenden und dann den Gesamtwert anpassen, indem Sie pro Biegung einen Kompensationswert hinzufügen. Hier beträgt die Kompensation -0,275, sodass aus 5 Zoll nach der Subtraktion 4,725 Zoll werden.

Definitionen:

Biegezugabe = Winkel * (π / 180) * (Radius + K-Faktor * Dicke) 

Biegekompensation = Biegezugabe – (2 * Rückschlag)

Innenversatz = tan (Winkel / 2) * Außenradius 

Zurückversatz = tan (Winkel / 2) * (Radius + Dicke)

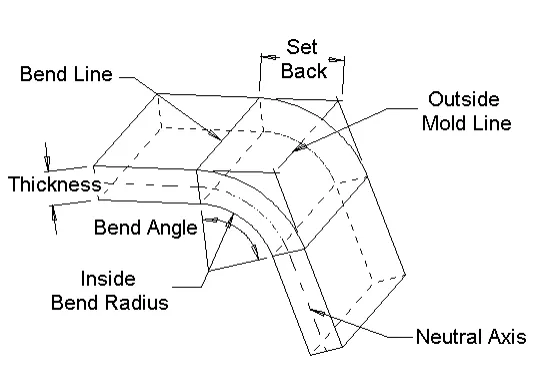
Biegezugabe – Die Länge des Bogens durch den Biegebereich an der neutralen Achse.

Biegewinkel – Der eingeschlossene Winkel des durch den Biegevorgang gebildeten Bogens.

Biegekompensation – Der Betrag, um den das Material durch den Biegevorgang gedehnt oder gestaucht wird. Es wird davon ausgegangen, dass die gesamte Dehnung oder Stauchung im Biegebereich erfolgt.

Biegelinien – Die geraden Linien auf der Innen- und Außenfläche des Materials, wo die Flanschgrenze auf den Biegebereich trifft.

Innerer Biegeradius – Der Radius des Bogens auf der Innenfläche des Biegebereichs.

K-Faktor – Definiert die Position der neutralen Achse. Sie wird als Abstand von der Innenseite des Materials zur neutralen Achse geteilt durch die Materialdicke gemessen.

Formlinien – Bei Biegungen unter 180 Grad sind die Formlinien die geraden Linien, an denen sich die den Biegebereich begrenzenden Flanschflächen schneiden. Dies geschieht sowohl auf der Innen- als auch auf der Außenfläche der Biegung.

Neutrale Achse – Betrachtet man den Querschnitt der Biegung, ist die neutrale Achse der theoretische Ort, an dem das Material weder komprimiert noch gedehnt wird.

Zurücksetzen – Bei Biegungen von weniger als 180 Grad ist der Rücksprung der Abstand von den Biegelinien zur Formlinie.

So berechnen Sie den „K“-Faktor:

Meines Wissens gibt es keine Formel zur Berechnung des K-Faktors. Ich bin mir sicher, dass irgendwo ein Mathematiker eine Formel hat. Aber sie ist für die meisten von uns wahrscheinlich zu komplex, um sie zu verstehen oder anwenden zu können.

Der K-Faktor ist der Prozentsatz der Materialdicke, bei dem es im Biegebereich weder zu einer Dehnung noch zu einer Stauchung des Materials kommt. Also die neutrale Achse!

Je härter das Material, desto geringer ist die Kompression auf der Innenseite der Biegung. Daher erfolgt eine stärkere Dehnung auf der Außenseite und die neutrale Achse verschiebt sich zur Innenseite der Biegung. Weichere Materialien ermöglichen eine stärkere Kompression auf der Innenseite und die neutrale Achse bleibt näher an der Mitte der Materialdicke.

Der Biegeradius hat einen ähnlichen Effekt. Je kleiner der Biegeradius, desto größer ist der Kompressionsbedarf und die neutrale Achse verschiebt sich zur Innenseite der Biegung. Bei einem größeren Radius bleibt die neutrale Achse nahe der Mitte der Materialdicke.

Generische K-Faktoren	Aluminium		Stahl
Radius	Weiche Materialien	Mittlere Materialien	Harte Materialien
Luftbiegen
0 bis Dicke	0.33	0.38	0.40
Dicke bis 3×Dicke	0.40	0.43	0.45
Größer als 3×Dicke	0.50	0.50	0.50
Bodenbildung
0 bis Dicke	0.42	0.44	0.46
Dicke bis 3×Dicke	0.46	0.47	0.48
Größer als 3×Dicke	0.50	0.50	0.50
Prägung
0 bis Dicke	0.38	0.41	0.44
Dicke bis 3×Dicke	0.44	0.46	0.47
Größer als 3×Dicke	0.50	0.50	0.50

Als gute Näherung für den K-Faktor beim Freibiegen kann anstelle der Tabelle folgende Formel verwendet werden:

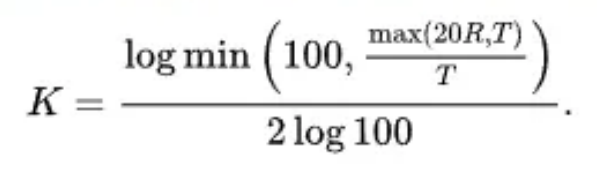
Diagramm und Berechnungsformeln für die Biegezugabe

Um Ihnen die Berechnungsformel für die Biegelänge einfacher und schneller zu machen, haben wir vier gängige Koeffiziententabellen zusammengestellt, sechzehn Berechnungsformeln für die Biegelänge veranschaulicht und einige Beispiele zum besseren Verständnis angeführt. Ich hoffe, die folgenden Inhalte helfen Ihnen in der Praxis. Bei Fragen stehen wir Ihnen gerne zur Verfügung.

V-Nutbreite\Plattendicke	0.6	0.8	1.0	1.2	1.5	2.0	2.5	3.0	3.5	4.0	4.5	5.0	Kleinste Größe
V4	0.9	1.4											2.8
V6		1.5	1.7	2.0									4.5
V7			1.8	2.1	2.4								5.0
V8			1.9	2.2	2.5								5.5
V10			2.1	2.3	2.7								7.0
V12			2.2	2.5	2.8	3.4							8.5
V14						3.5	3.8			6.4	6.8		10.0
V16					3.1	3.8	4.5	5.0					11.0
V18					3.3	4.0							13.0
V20						4.0	4.9	5.1		6.6	7.2	7.8	14.0
V25						4.4	5.0	5.5		6.8	7.8	8.3	16.5
V32						5.0	5.5	6.1		8.7

Notiz: Wenn die grafische Teilegröße mit negativer Toleranz markiert ist, kann der Biegefaktorwert erhöht werden, wie in der Tabelle gezeigt. Der rote Teil kann auf 2,8, 2,82, 3,4, 3,43 oder 3,44:4,5, 4,6, 5,5:5,6 erhöht werden.

Dicke mm\Winkel	Formnut Breite		90°	Innenecke	Außenecke		180°
1.5	V10		3.0	3.2	4.1		0.8
2.0	V12		3.8	3.7	4.6		1.0
2.5	V16		4.5	4.8	6.1		1.3

Dicke  mm\Winkel	30°		45°		60°			120°			135°			145°
1.0	0.35		0.7		1.1			1.0			0.6			0.4
1.2	0.4		0.8		1.2			1.0			0.6			0.4
1.5	0.5		1.0		1.6			1.4			0.9			0.6
2.0	0.6		1.2		2.0			1.7			1.1			0.7
2.5	0.8		1.6		2.6			2.2			1.4			0.85
3.0	1.0		2.2		3.4			2.8			2.0			1.2
4.0								3.7			2.4			1.4

Dicke mm		0.5	1.0	1.2		1.5	2.0		2.5	3.0		4.0	5.0		6.0
Prozessloch mm		1. Keine Löcher 2.Kann φ2-Loch öffnen		φ2		φ2,5	φ3,0		φ3,5	φ4.0		φ5,5	φ6,0		φ7,0

Notiz: Wenn besondere Anforderungen bestehen, kann eine größere Blendengröße verwendet werden.

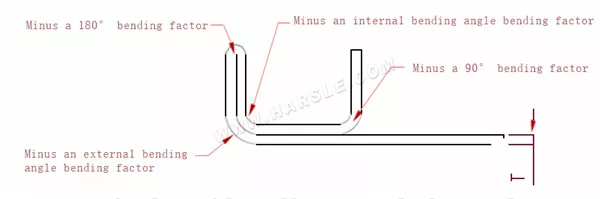
Diagramm und Berechnungsformel für einen Bogen

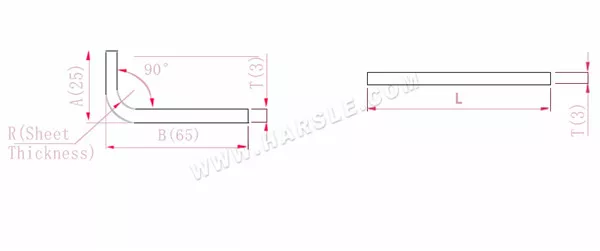
A, B – Biegelänge des Werkstücks

P' – Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Die erweiterte Länge L=A+B-P', also L=25+65-5,5=84,5

Gemäß Tabelle 1 beträgt die Plattendicke 3, die untere Matrize V25 und der Biegekoeffizient 5,5

Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Diagramm und Berechnungsformel des Zweibogens

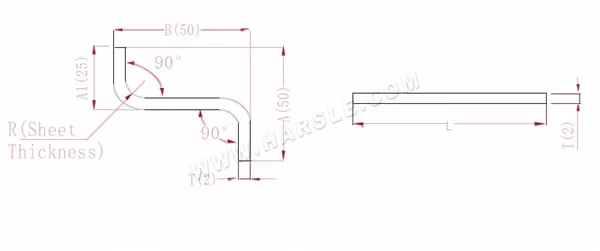
A(A1), B— Biegelänge des Werkstücks

P' – Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Die erweiterte Länge L=A+T+B-2*P', also L=50+2+50-2*3,4=95,2

Gemäß Tabelle 1 beträgt die Plattendicke 2, die untere Matrize V12 und der Biegekoeffizient 3,4

Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Diagramm und Berechnungsformel des Dreibogens

A(A1), B (B1) – Biegelänge des Werkstücks

P' – Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Die erweiterte Länge L=A+T+B+T-3*P', also L=50+2+90+2-3*3,4=133,8

Gemäß Tabelle 1 beträgt die Plattendicke 2, die untere Matrize V12 und der Biegekoeffizient 3,4

Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Diagramm und Berechnungsformel des Vierbogens 

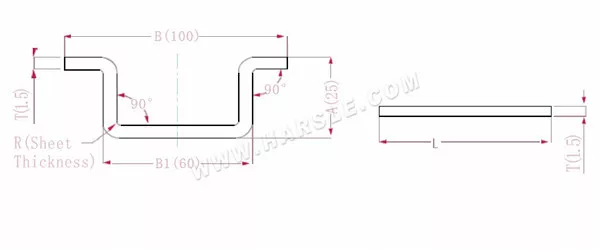
A, B (B1) – Biegelänge des Werkstücks

P' – Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Die erweiterte Länge L=A+A+B+T+T-4*P', also l = 25+25+100+1,5+1,5-4 * 2,8 = 141,8

Gemäß Tabelle 1 beträgt die Plattendicke 1,5, die untere Matrize ist V12 und der Biegekoeffizient beträgt 2,8

Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Diagramm und Berechnungsformel des Sechsbogens 

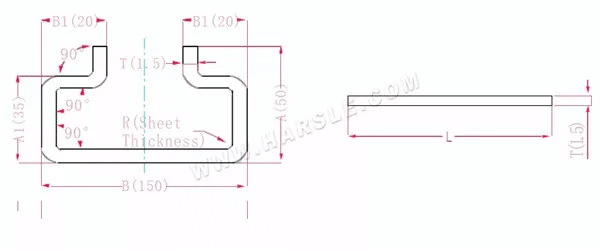
A(A1), B (B1) – Biegelänge des Werkstücks

P' – Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Die Expansionslänge L=A+T+A+T+B+B1+B1-6*P‘

das ist l = 50+1,5+50+1,5+150+20+20-6 * 2,8 = 276,2

Gemäß Tabelle 1 beträgt die Plattendicke 1,5, die untere Matrize ist V12 und der Biegekoeffizient beträgt 2,8

Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Diagramm und Berechnungsformel der Biegung um 180 Grad

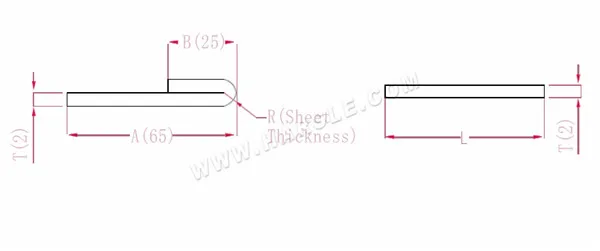
A, B – Biegelänge des Werkstücks

P' – Abflachungs-Kehlenbiegungskoeffizient

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Die erweiterte Länge L=A+B-P', also L=25+65-1=89

Gemäß Tabelle 2 beträgt die Plattendicke 2, die untere Matrize ist V12 und der Biegefaktor beträgt die Hälfte der Plattendicke

Hinweis: Gemäß Tabelle 2 ergeben sich durch die Auswahl unterschiedlicher Unterwerkzeuge unterschiedliche Biegekoeffizienten und unterschiedliche Plattendicken.

Diagramm und Berechnungsformel der Doppellagenbiegung 

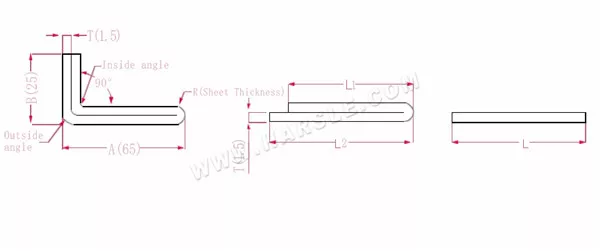
A, B – Biegelänge des Werkstücks

P1 – Biegekoeffizient der Innenecke

P2 – Biegekoeffizient des äußeren Biegewinkels

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Die erweiterte Länge L1=(A-1,5) +(B-1,5)-P1, also L1= (65-1,5) +(25-1,5)-3,2=83,8

L2=A+B-P2, also L2=65+25-4,1=85,9

L=L1+L2-T/2, also L=83,8+85,9-0,75=168,95

Gemäß Tabelle 2 beträgt die Plattendicke 1,5, die untere Matrize V12, der Biegekoeffizient der inneren Ecke 3,2, der Biegekoeffizient der äußeren Ecke 4,1 und der Biegekoeffizient bei 180 Grad 0,75.

Hinweis: Gemäß Tabelle 2 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Diagramm und Berechnungsformel der zweilagigen Biegung mit einer Kante

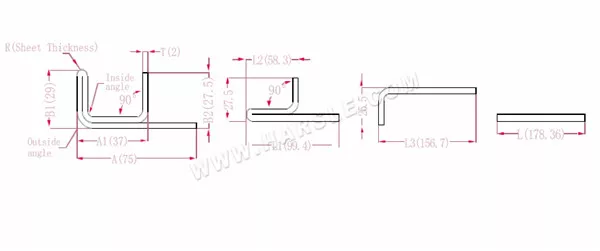
A, A1, A2, B1, B2, L, L1, L2, L3 – Biegelänge des Werkstücks

P1 – Biegekoeffizient der Innenecke

P2 – Biegekoeffizient des äußeren Biegewinkels

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Die erweiterte Länge L1=(A1-T) +(B2-T)-P1, also L1= (35-2) +(34-2)-3,7=61,3

L2=(B1-T) +(A2-T)-P1, also L2= (50-2) +(34-2)-3,7=76,3

L3=A+B1+B2-2*P2, also L3=70+35+50-2*4,6+145,8

L=L1+L2+L3-2*P3, also L=61,3+75,3+145,8-2*1=280,4

Gemäß Tabelle 2 beträgt die Plattendicke 2, die untere Matrize V12, der innere Eckbiegekoeffizient 3,7, der äußere Eckbiegekoeffizient 4,6 und der 90-Grad-Biegekoeffizient 1.

Hinweis: Gemäß Tabelle 2 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Diagramm und Berechnungsformel der zweilagigen Biegung mit zwei Kanten

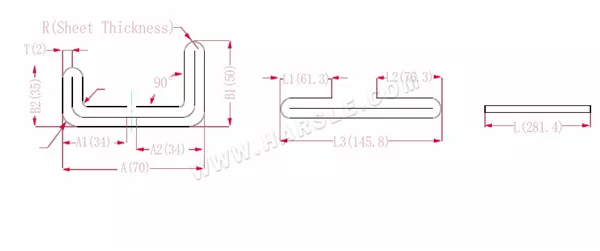
A, A1, A2, B1, B2, L, L1, L2, L3 – Biegelänge des Werkstücks

P1 – Biegekoeffizient der Innenecke

P2 – Biegekoeffizient des äußeren Biegewinkels

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Die erweiterte Länge L1=(A1-T) +(B2-T)-P1, also L1= (35-2) +(34-2)-3,7=61,3

L2=(B1-T) +(A2-T)-P1, also L2= (50-2) +(34-2)-3,7=76,3

L3=A+B1+B2-2*P2, also L3=70+35+50-2*4,6+145,8

L=L1+L2+L3-2*P3, also L=61,3+75,3+145,8-2*1=280,4

Gemäß Tabelle 2 beträgt die Plattendicke 2, die untere Matrize V12, der innere Eckbiegekoeffizient 3,7, der äußere Eckbiegekoeffizient 4,6 und der 90-Grad-Biegekoeffizient 1.

Hinweis: Gemäß Tabelle 2 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Diagramm und Berechnungsformel der Stufenbiegung

A, B – Biegelänge des Werkstücks

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Entfaltete Länge L=A+1

Hinweis: Wenn der Schritt der Dicke zweier Platten entspricht, addieren Sie 0,5 für jeden Schritt und 1 für jeden Schritt.

Diagramm und Berechnungsformel für die Biegung des Sonderwinkels 1

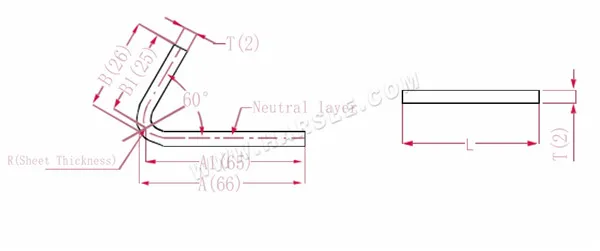
A(A1), B (B1) – Biegelänge des Werkstücks

P' – Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Die Expansionslänge L=(AT) +(BT)-P', also L= (66-1) +(26-1)-2=65+25-2=88

Gemäß Tabelle 3 beträgt die Plattendicke 2, die untere Matrize V12 und der 60-Biegekoeffizient 2

Hinweis: Gemäß Tabelle 3 wird die neutrale Schicht als Biegelänge und -breite gewählt.

Diagramm und Berechnungsformel der Biegung Sonderwinkel 2

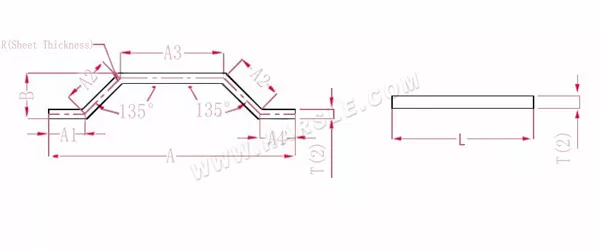
A (A1, A2, A3, A4), B— Biegelänge des Werkstücks

P— Biegefaktor von 135 Biegewinkeln

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Die Expansionslänge L = A1+A2+A3+A2+A4-PP.

Hinweis: Der gleiche Druckschritt Biegen muss nur zwei Koeffizienten reduzieren

Gemäß Tabelle 3 beträgt die Plattendicke 2, die untere Matrize V12 und der Biegekoeffizient bei 135 beträgt 1,1.

Diagramm und Berechnungsformel der Biegung Sonderwinkel 3

A (A1, A2), B (B1, B2) – Biegelänge des Werkstücks

P1 – 120°-Biegekoeffizient

P2 – 145°-Biegekoeffizient

P3 – 90°-Biegekoeffizient

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

Hinweis: Wenn die Grafikgröße auf der Form markiert ist, sollte die Formgröße bei der Berechnung der Entfaltungslänge in die neutrale Schichtgröße umgewandelt werden.

Die Expandlänge L=A11+B11+B21+A21-P1-P2-P3, also l = 80+50+103+70-1,7-0,7-3,4 = 297,2

Gemäß Tabelle 3: Die Plattendicke beträgt 2, die untere Matrize ist V12, der 120-Biegekoeffizient beträgt 1,7, der 145-Biegekoeffizient beträgt 0,7 und der 90-Biegekoeffizient beträgt 3,4

Hinweis: Gemäß Tabelle 3 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Diagramm und Berechnungsformel der gemeinsamen Bindung 1

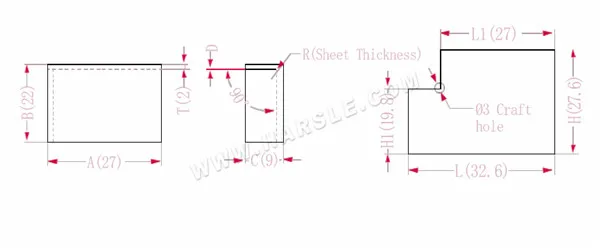
A, B, C – Länge, Breite und Höhe der Biegekante des Werkstücks

P – Biegekoeffizient

R – Biegung und Rundung (im Allgemeinen Plattendicke)

H(H1), l (L1) – die entfaltete Länge jeder Seite

T – Materialstärke

D – Biegeprozessspiel (im Allgemeinen 0–0,5)

Die erweiterte Länge L1=A, also L1=27

L=A+CP, also L=27+9-3,4=32,6

H1=BTD, also H1=22-2-0,2=19,8. Hinweis: D ist 0,2.

H=B+CP, also H=22+9-3,4=27,6

Gemäß Tabelle 1: Die Plattendicke beträgt 2, die Unterform ist V12 und der Biegekoeffizient beträgt 3,4

Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Diagramm und Berechnungsformel der gemeinsamen Bindung 2

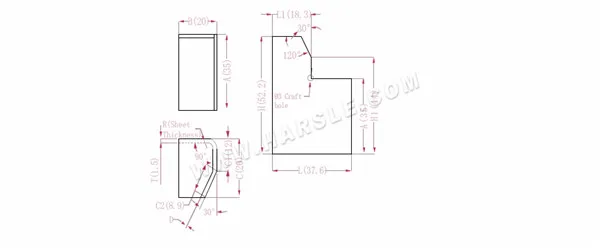
A, B, C – Länge, Breite und Höhe der Biegekante des Werkstücks

H(H1), L (L1) – die entfaltete Länge jeder Seite

P – 90°-Biegekoeffizient P1 – 30°-Biegekoeffizient

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

D – Biegeprozessspiel (im Allgemeinen 0–0,5)

Die erweiterte Länge L1=BTD, also L1=20-1,5-0,2=18,3

L=B+C1+C2-P-P1, also L=20+12+8,9-2,8-0,5=37,6

H1=C1+APD, also H1=12+35-2,8-0,2=44. Hinweis: D ist 0,2.

H=A+CP, also H=35+20-2,8=52,2

Gemäß Tabelle 1: Die Plattendicke beträgt 1,5, die untere Matrize ist V12, der Biegekoeffizient beträgt 2,8 und der 30-Biegekoeffizient beträgt 0,5

Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Diagramm und Berechnungsformel der gemeinsamen Bindung 3

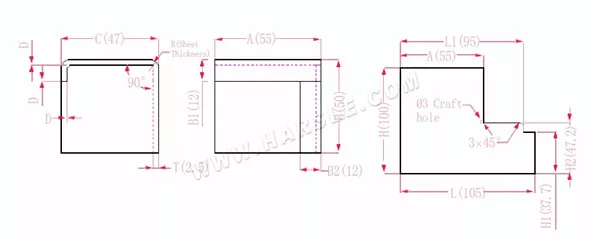
A, B, C – Länge, Breite und Höhe der Biegekante des Werkstücks

H(H1), L (L1) – die entfaltete Länge jeder Seite

P – Biegekoeffizient

R – Biegung und Rundung (im Allgemeinen Plattendicke)

T – Materialstärke

D – Biegeprozessspiel (im Allgemeinen 0–0,5)

Die erweiterte Länge H1=B-B1-D beträgt H1=50-12-0,3=37,7. Hinweis: D ist 0,2.

H2=BTD, also H2=50-2,5-0,3=47,2

H=B+C+B1-2*P, also H=50+47+12-2*4,5=100

L1=A+CTDP, also L1=55+47-2,5-0,3-4,5=94,7

L=A+C+B2-2*P, also L=55+47+12-2*4,5=105

Gemäß Tabelle 1: Die Plattendicke beträgt 1,5, die Unterform ist V16 und der Biegekoeffizient beträgt 4,5

Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

Videodemo