Entwurf einer Schwanenhals-Biegeform und Intensitätsanalyse
Mit der breiten Anwendung der Schwanenhals-Biegematrize Im Bereich des Stanzens werden die Herstellungskosten der gebogenen Formteile erheblich reduziert. Gleichzeitig ist das Problem der Formschäden, das bei der Verwendung der Schwanenhals-Biegeform auftritt, zu einem häufigen Trägheitsproblem in der Produktionswerkstatt geworden, und der Schaden wird durch eine unzureichende Formfestigkeitskonstruktion und eine unangemessene Formkonstruktionsstruktur verursacht.
1. Prozessanalyse von Teilen
Am Beispiel der Seitensäule eines Güterwagens werden der Konstruktionsprozess und die Kraftanalyse der Schwanenhals-Biegematrize werden detailliert beschrieben. Abbildung 1 zeigt den Querschnitt der Seitensäule des Exportwaggons. Die Dicke beträgt 12 mm. Das Material ist Q450NQR1. Der hochfeste und korrosionsbeständige Stahl für Eisenbahnwaggons hat eine Länge von 2530 mm. Der Prozessablauf ist: Kugelstrahlen, Lackieren → Schneiden → Schneiden → Richten → Biegen → Lagern.
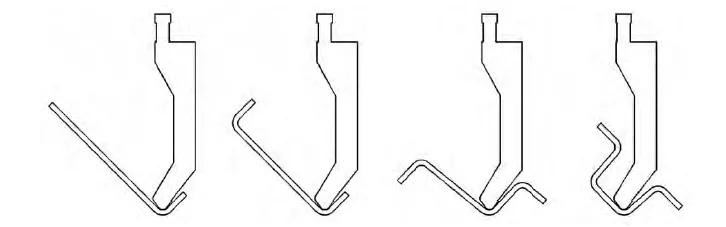
Wie in Abb. 2 dargestellt, ist der Biegevorgang in vier Schritte unterteilt. Während des Biegevorgangs in Schritt 4 spielt der Schwanenhals-Biegemodus eine Rolle. Daher erfolgt im Entwurfsprozess des Schwanenhals-Biegewerkzeugs die Parameterauslegung des Schwanenhals-Biegewerkzeugs hauptsächlich gemäß Schritt 4.
2. Berechnung der Biegekraft
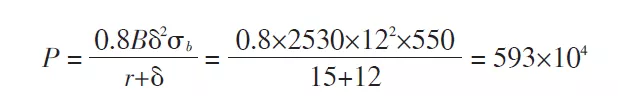
P——Gesamtbiegekraft, N
B——Biegebreite, mm
δ——Materialdicke, mm
σb——Zugfestigkeit, MPa
R——innerer Biegeradius, mm
Die für die Berechnung des Teils erforderliche Biegekraft beträgt 5930 kN, was bedeutet, dass das Biegewerkzeug einem Druck von 5930 kN der Biegemaschine standhalten muss.
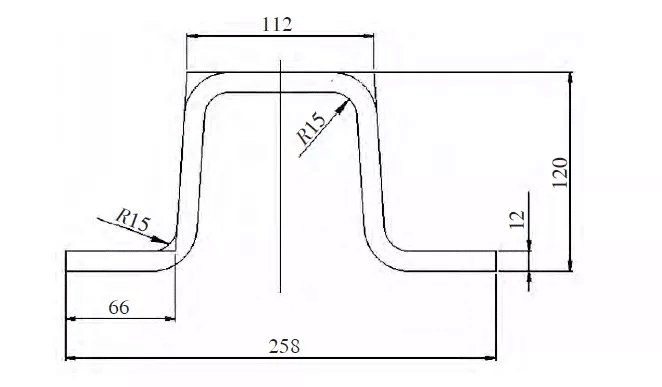
3. Konstruktionsprinzip der Schwanenhals-Biegeform
Wie in Biegeschritt 4 in Abb. 2 gezeigt, stört das Werkstück den Biegevorgang, wenn kein Schwanenhalsstrukturteil vorhanden ist. Dadurch wird der Biegevorgang abgebrochen und das Werkstück kann nicht mehr geformt werden. Das Konstruktionsprinzip der Schwanenhalsform besteht darin, den Schwanenhalsteil der Form zu verwenden, um zu vermeiden, dass das Werkstück während des Formgebungsprozesses mit der Form kollidiert.
4. Bestimmung der Parameter der Schwanenhals-Biegeform
Wie in Abb. 3 dargestellt, handelt es sich um eine schematische Darstellung eines Schwanenhals-Biegewerkzeugs. Die Exzentrizität L und die Breite t des Schwanenhalses sind die wichtigsten Parameter, die die Festigkeit des Werkzeugs beeinflussen. Um den Anforderungen der Formteile gerecht zu werden, beträgt die anfängliche Schwanenhalsbreite 50 mm und die Exzentrizität L des Schwanenhalses sollte (t/2+2,5) mm betragen, wobei t die Breite des am weitesten vom Druckmittelpunkt entfernten Formabschnitts ist, d. h. t = 50 mm.
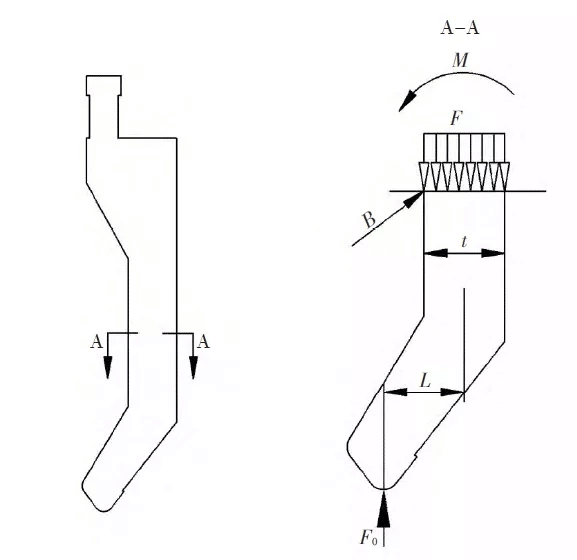
5. Intensitätsanalyse
Es wird eine Festigkeitsanalyse des Schwanenhalsabschnitts der Form durchgeführt. Zusätzlich zum Druck der Biegemaschine wirkt auf die Form ein Biegemoment, das durch den Druck im Schwanenhalsabschnitt verursacht wird. Wählen Sie Abschnitt AA des Schwanenhalses für die Festigkeitsanalyse aus und berechnen Sie die Spaltengleichung: Bei der Festigkeitsanalyse des Schwanenhalsabschnitts der Form wirkt auf die Form zusätzlich zum Druck der Biegemaschine auch ein Biegemoment. Wie in Abb. 4 dargestellt, zeigt die Analyse des Spannungszustands AA des gefährlichen Abschnitts des Schwanenhalses, dass die Abschnittsbreite t beträgt, der vertikale Abstand zwischen dem Druckmittelpunkt der Biegemaschine und dem Schwerpunkt des Abschnitts AA L ist, der von der Biegemaschine auf die Biegematrize ausgeübte Druck F ist, die Reaktionskraft F0 des Werkstücks auf die Biegematrize, das Biegemoment des Abschnitts M ist und an Punkt B des Abschnitts die Möglichkeit eines Bruchs besteht. Nach der Analyse wird ein vereinfachtes Diagramm des Kraftzustands des in Abb. 4 dargestellten Abschnitts AA gezeichnet.
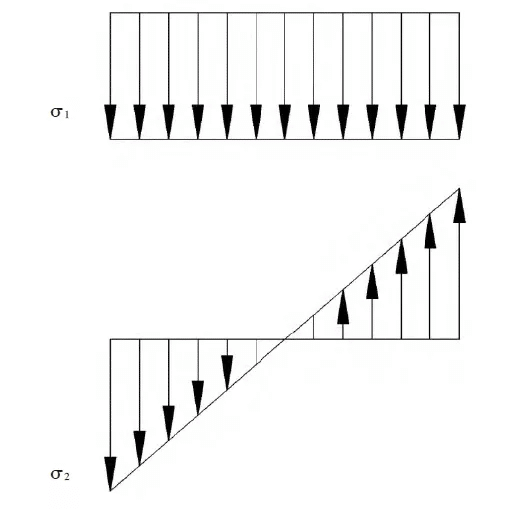

σ1——Spannung, die durch die äußere Kraft F0 erzeugt wird
σ2 – die durch das Biegemoment erzeugte Spannung
In Gleichung (5) ist W der Biegequerschnittskoeffizient. Da der Querschnitt AA ein Rechteck mit der Höhe t und der Länge h ist, gilt w = t2h/6.
Aus Formel (2) folgt M=F0×L. Setzen Sie W und M in die Formel ein:
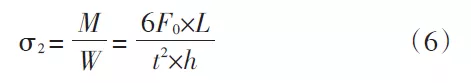
t——die Dicke des A-Abschnitts, mm
L——der vertikale Abstand zwischen dem Druckzentrum der Biegemaschine und dem Schwerpunkt des A-Abschnitts, mm
h——die Länge des Biegewerkzeugs, mm
Das Einsetzen der Werte σ1 und σ2 in Gleichung (3) ergibt σ3 als:
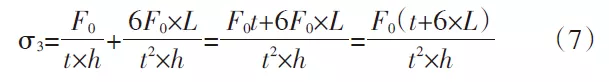
σ3 – die Summe aus Biegemoment und Spannung, die durch M und die äußere Kraft F0 erzeugt wird
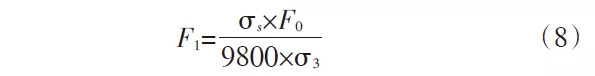
F1——Maximale Belastung, der der gefährliche Abschnitt AA der Form standhalten kann
δs – die Streckgrenze des Biegemodusmaterials
Durch Einsetzen des Ergebnisses σ3 der Formel (7) in die Formel (8) erhält man F1
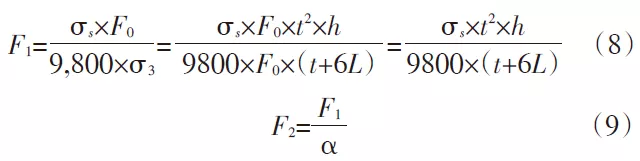
In Formel (9) ist α der Sicherheitsfaktor, der üblicherweise einen Wert zwischen 1,1 und 1,2 annimmt. In dieser Berechnung wird α=1,15 angenommen und die Werte α und F1 werden in Formel (9) eingesetzt:
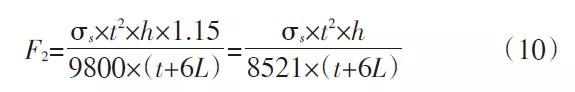
δs = 450 MPa, h = 2530 mm, t = 50 mm, L = 27,5 mm. Wird dies in Formel (10) eingesetzt, beträgt der F2-Wert 1553 t. Dies bedeutet, dass der entworfene AA-Abschnitt mit großer Biegekraft einer Spannung von 1553 t standhalten kann. Dieser Wert ist viel größer als die Biegekraft beim Formen des Teils und kann die Formanforderungen des Teils erfüllen.
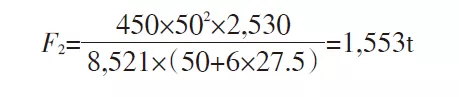
6. Strukturoptimierung
Gemäß den obigen Berechnungsergebnissen beträgt die Spannung des gefährlichen Abschnitts AA 15530 kN, was viel größer ist als die Biegekraft der Werkstückformung von 5930 kN, wodurch die Formanforderungen des Werkstücks erfüllt werden können.
Um jedoch die Arbeitsintensität des Bedieners weiter zu reduzieren und die Herstellungskosten der Form zu senken, ist es notwendig, das Design der Form zu optimieren, damit sie die Realisierung des Produkts erfüllen kann, die
Arbeitsintensität des Bedieners und Reduzierung der Herstellungskosten der Form.
Gemäß Formel (10) hängt die Spannung im gefährlichen Abschnitt AA von der Streckgrenze σs des Formmaterials, der Dicke t des Abschnitts A, der Länge h des Biegemodus und dem vertikalen Abstand L zwischen dem Druckzentrum der Biegemaschine und dem Schwerpunkt des Abschnitts A ab. Da das Formmaterial normalerweise nicht geändert wird, ist σs ein fester Wert. Die Länge des Werkstücks beträgt 2530 mm, was ebenfalls ein fester Wert ist: L = t/2 + 2,5. Daher ist die Variable in der Formel nur t, und der Wert von t wird schrittweise optimiert:
Führen Sie eine Neuberechnung durch, indem Sie den Wert von t von 50 auf 30 ändern:

Zur Neuberechnung den Wert von t von 30 auf 25 umrechnen:
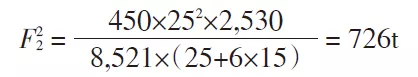
Führen Sie eine Neuberechnung durch, indem Sie den Wert von t von 25 auf 20 ändern:
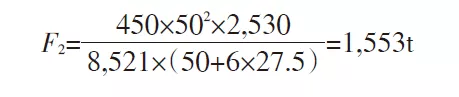
Aus den obigen Berechnungsergebnissen ist ersichtlich, dass F32 kleiner ist als die maximale Biegekraft beim Formen des Teils und F12 und F22 größer als die maximale Biegekraft beim Formen des Teils. Die Herstellungskosten der Form sind jedoch gering, was dem Bediener den Ein- und Ausbau der Form erleichtert. Daher wurde schließlich festgestellt, dass der gefährliche Abschnitt AA der Form eine Breite von 25 mm hat. Die Dicke des Arbeitsteils des verbleibenden Teils der Form ist auf 25 mm ausgelegt. Die Krümmung des Schwanenhalses ist übermäßig gekrümmt, um lokale Spannungskonzentrationen zu vermeiden. Die Größe der Schnittstelle zwischen Form und Gerät kann entsprechend dem Klemmmechanismus des Geräts ausgelegt werden.
7. Wirkungsüberprüfung
Die Praxis hat bewiesen, dass die Form dem Spannungszustand des gebogenen Teils standhält und ihre Steifigkeit und Festigkeit den tatsächlichen Produktionsanforderungen entsprechen. Um sich an die Hauptmelodie der heutigen hocheffizienten, kostengünstigen und schnelllebigen Teilefertigungswerkstatt anzupassen, ist die Formenkonstruktion als Kostenquelle ein wichtiger Bestandteil der Teilekosten. Die Formel und der Berechnungsprozess können im Konstruktionsprozess der Schwanenhalsform gefördert und angewendet werden.
8. Fazit
Der gefährliche Abschnitt des Schwanenhals-Biegewerkzeugs ist am weitesten vom Druckzentrum entfernt. Unter der Bedingung eines bestimmten Formmaterials und einer bestimmten Formstruktur ist die Festigkeit des gefährlichen Abschnitts proportional zur Dickenabmessung des gefährlichen Abschnitts.





















