Nach meiner Erfahrung in der Arbeit mit NutbiegenDie Berechnung der ungefalteten Länge ist entscheidend für präzise Ergebnisse in der Metallverarbeitung. Die ungefaltete Länge bestimmt, wie viel Material vor dem Biegen benötigt wird. Eine korrekte Berechnung ist entscheidend, um Abfall zu vermeiden und die richtige Passform zu gewährleisten. Im Laufe der Jahre habe ich einen systematischen Ansatz zur Berechnung der entfaltete Länge der Nutbiegung unter Berücksichtigung von Faktoren wie Biegeradius und Materialstärke. In diesem Artikel teile ich meine Erkenntnisse zur Berechnung der ungefalteten Länge der Nutbiegung und gebe praktische Tipps, die Ihre Biegegenauigkeit in verschiedenen Anwendungen verbessern können.

Rillenbiegen verstehen

Bevor wir uns in die Berechnungen vertiefen, ist es wichtig zu verstehen, was das Rillenbiegen beinhaltet. Bei diesem Verfahren wird entlang des Materials eine Rille erzeugt, um das Biegen in einem bestimmten Winkel zu ermöglichen. Die Rille hilft in der Regel dabei, die Biegung zu kontrollieren und eine sauberere, präzisere Faltung zu gewährleisten. Um jedoch den gewünschten Winkel und die gewünschte Form zu erreichen, müssen Sie die korrekte ungefaltete Länge des Materials kennen.

Die Formel für die entfaltete Länge

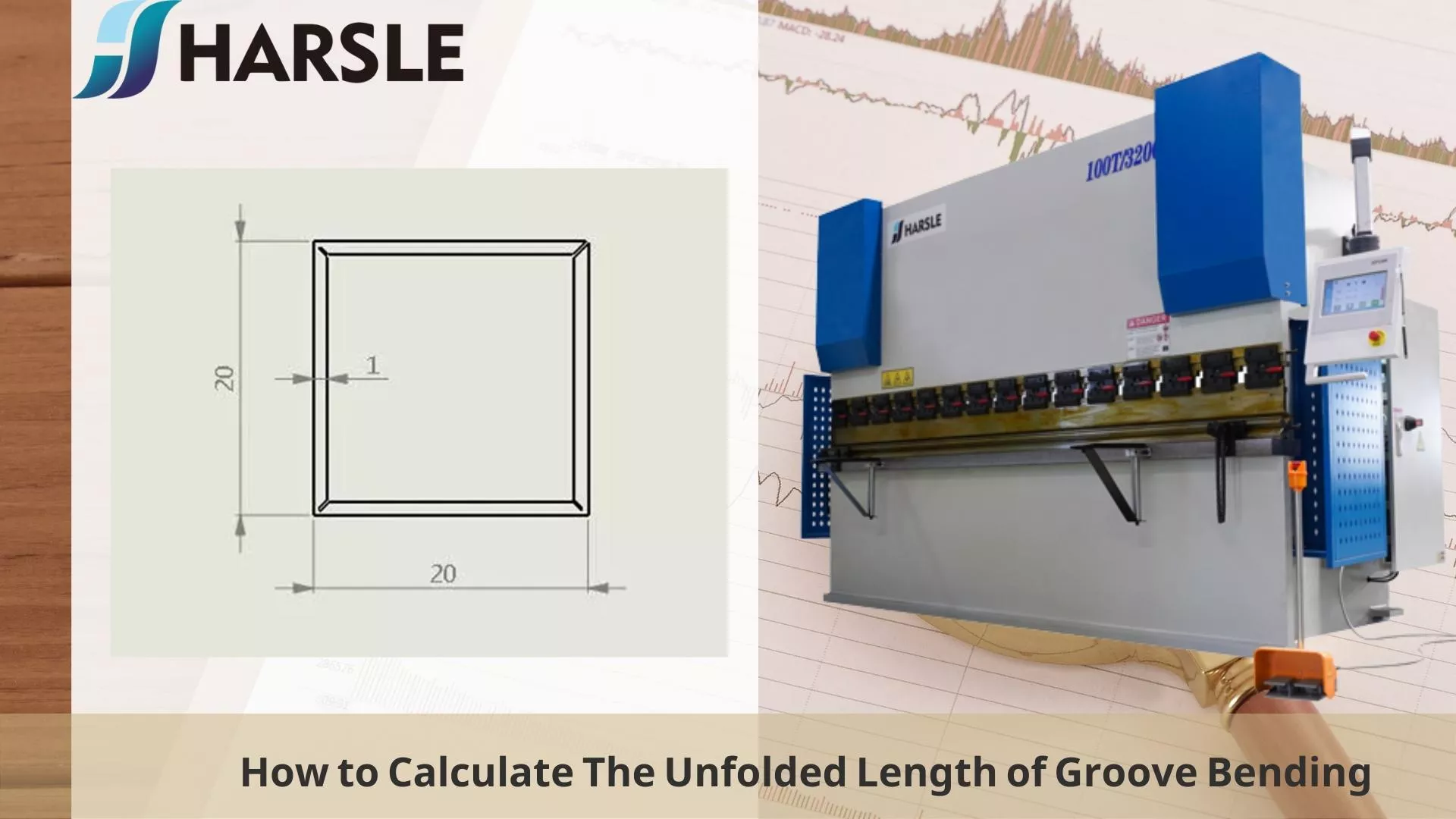
Wie in der Abbildung dargestellt, wird nun mittels Hobeln ein 20×20 Quadratrohr mit einer Blechstärke von 1mm gebogen.

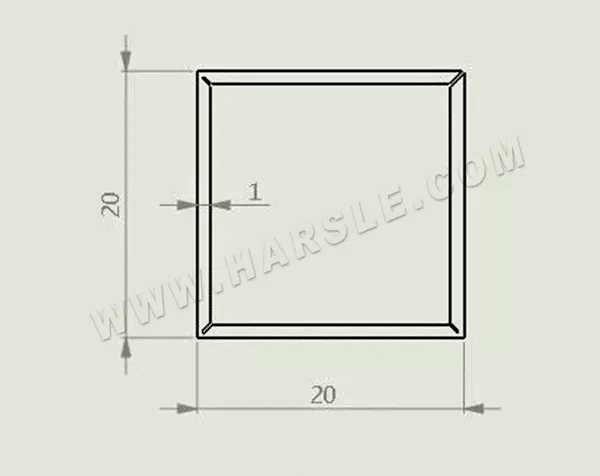
Die verbleibende Materialstärke a der Hobelnut hängt von der Größe des rechtwinkligen Bogens nach dem Biegen durch den Kunden und auch von der Größe der Materialstärke t ab. Im Allgemeinen gilt: Wenn die Materialstärke kleiner oder gleich 1 mm ist, ist a = 0,4 mm, und wenn die Materialstärke größer als 1 mm ist, ist a = t/2.

L=2×(L1+L2)=2x((Seitenlänge-1xa-0,2)+(Seitenlänge-2xa)) des dargestellten Beispiels

=2x((20-1×0,4-0,2)+(20-2×0,4))=77,2mm

Hinweis: Ein Ende von L1 wird abgehobelt, egal wie dick das Material ist, es werden 0,2mm abgezogen

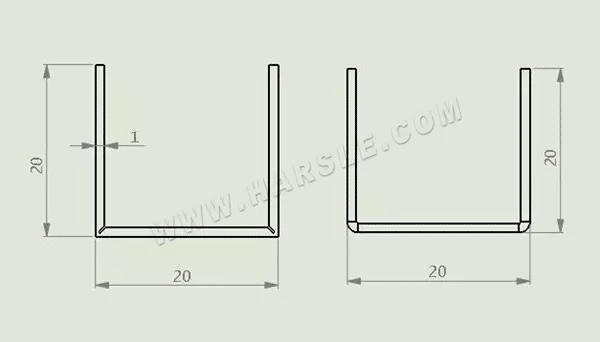
Vergleichen wir den Unterschied zwischen der Berechnung der Biegung und Entfaltung durch geschlitzte Biegung und ungeschlitzte Biegung:

Bei Schlitzbögen wird die Gesamtlänge folgendermaßen berechnet:

L=20-0,4+20-2X0,4+20-0,4=58,4

Bei nicht geschlitzten Bögen lautet die Berechnungsmethode für die Gesamtlänge:

●L=(20-1xt+k)+(20-2xt+2xk)+(20-1xt+1xk)=(20-1+0,2)+(20-2+2×0,2)+(20-1+ 0,2)=56,8 mm

●t ist die Materialdicke, k ist der Koeffizient. Die Größe von k hängt mit der Materialdicke zusammen und liegt im Allgemeinen zwischen 0,2 und 0,25. Je dicker das Material, desto höher der K-Wert. In diesem Beispiel wird k als 0,2 ausgewählt.

Das Folgende ist eine Kombination aus einem Z-förmigen Schlitz und keinem Schlitz, um die entfaltete Länge der Biegung zu berechnen:

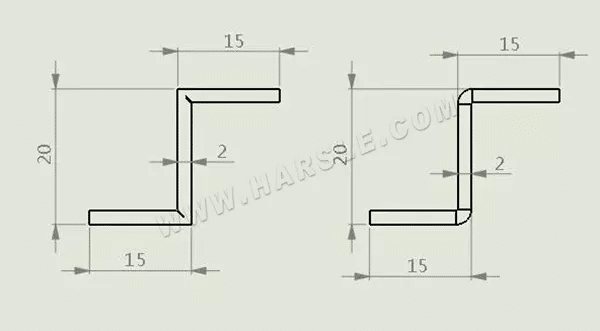
Bei der 2mm Platte wird die verbleibende Materialstärke a der Hobelnut mit t/2=1mm angenommen, (wenn der Kunde einen kleineren geraden Bogen wünscht, sollte der a-Wert kleiner als 1mm gewählt werden) Somit ergibt sich die Dehnungslänge:

L=15-1+20-2×1+15-1=46mm

Für eine 2 mm dicke Platte ohne Nuten und Biegungen wird der Koeffizient k mit 0,25 gewählt, also die ungefaltete Länge:

L=(15-2+0,25)+(20-2×2+2×0,25)+(15-2+0,25)=43mm

Die Berechnungsmethode wird im Folgenden anhand eines Beispiels für das Nuten und Nichtnuten eines mehrfach gebogenen Werkstücks beschrieben:

Bei der 3 mm dicken Platte wird davon ausgegangen, dass der Kunde einen kleineren rechtwinkligen Bogen benötigt, dann beträgt die verbleibende Materialdicke 0,5 mm und die erweiterte Länge L=(40-0,5)+(30-2×0,5)+(30-2×0,5) +(10-0,5)=107 mm;

Für eine 3 mm dicke Platte wird der Koeffizient k mit 0,25 gewählt, also die entfaltete Länge:

L=(40-3+0,25)+(30-6+2×0,25)+(30-6+2×0,25)+(10-3+0,25)=93,5mm

Nachfolgend ist ein Beispiel für das Rückbiegen nach dem Nuten dargestellt, um die Methode zur Berechnung der Ausdehnung vorzustellen:

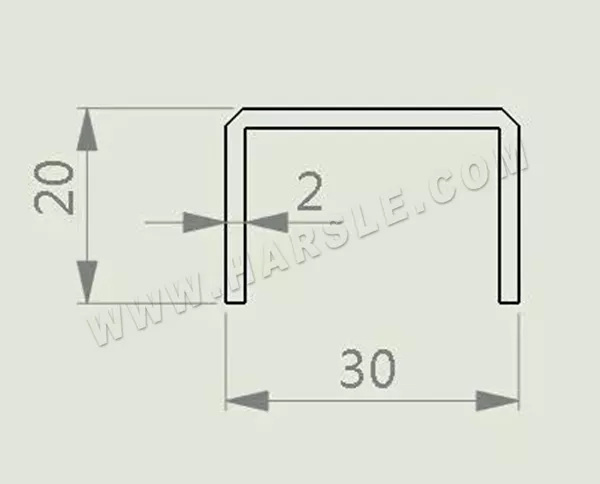
Für Rückbiegungen nach dem Fugenhobeln wie abgebildet

Berechnen Sie die Länge der Erweiterung als

L=(20-2+0,2)+(30-2×2+2×0,2)+(20-2+0,2)=62,8 mm