Conception d'une matrice de pliage à col de cygne et analyse d'intensité
Avec la large application de la matrice de pliage à col de cygne Dans le domaine de l'emboutissage, le coût de fabrication des pièces courbes est considérablement réduit. Parallèlement, les dommages aux moules survenant lors de l'utilisation de matrices de pliage à col de cygne sont devenus un problème d'inertie courant dans les ateliers de production. Ces dommages sont dus à une conception insuffisante et à une structure de moule déraisonnable.
1. Analyse du processus des pièces
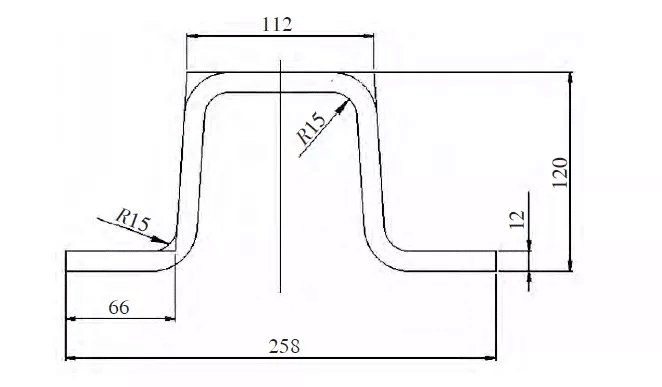
En prenant comme exemple la colonne latérale d'un wagon de marchandises ferroviaire, le processus de conception et l'analyse des forces de la matrice de pliage à col de cygne sont décrits en détail. La figure 1 montre la section transversale de la colonne latérale d'un wagon d'exportation. L'épaisseur est de 12 mm. Le matériau utilisé est le Q450NQR1. Cet acier haute résistance et résistant à la corrosion pour wagons a une longueur de 2 530 mm. Le processus est le suivant : grenaillage, peinture → découpe → découpe → planage → pliage → stockage.
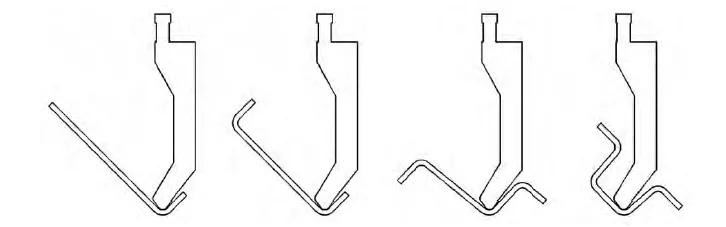
Comme le montre la figure 2, le processus de pliage est divisé en quatre étapes. Lors de l'étape 4, le mode de pliage en col de cygne joue un rôle important. Par conséquent, lors de la conception de la matrice de pliage en col de cygne, la conception des paramètres de la matrice est principalement réalisée selon l'étape 4.
2. Calcul de la force de flexion
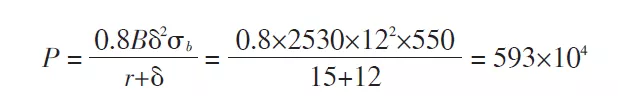
P——force de flexion totale, N
B——largeur de courbure, mm
δ——épaisseur du matériau, mm
σb——résistance à la traction, MPa
R——rayon de courbure intérieur, mm
La force de pliage requise pour le calcul de la pièce est de 5930 kN, ce qui signifie que la matrice de pliage doit résister à 5930 kN de pression de la machine de pliage.
3. Principe de conception du moule de pliage à col de cygne
Comme illustré à l'étape 4 du pliage (figure 2), en l'absence de col de cygne, la pièce interférera avec le pliage, ce qui interrompra le pliage et empêchera le formage de la pièce. Le principe de conception du moule à col de cygne est d'utiliser ce col de cygne pour éviter toute interférence de la pièce avec le moule pendant le formage.
4. Détermination des paramètres de la matrice de pliage à col de cygne
Comme le montre la figure 3, le schéma d'une matrice de pliage à col de cygne présente l'excentricité L et la largeur t du col de cygne comme paramètres clés de sa résistance. Pour répondre aux besoins de formage des pièces, la largeur initiale du col de cygne est de 50 mm et son excentricité L doit être de (t/2+2,5) mm, où t est la largeur de la section du moule la plus éloignée du centre de pression, soit t = 50 mm.
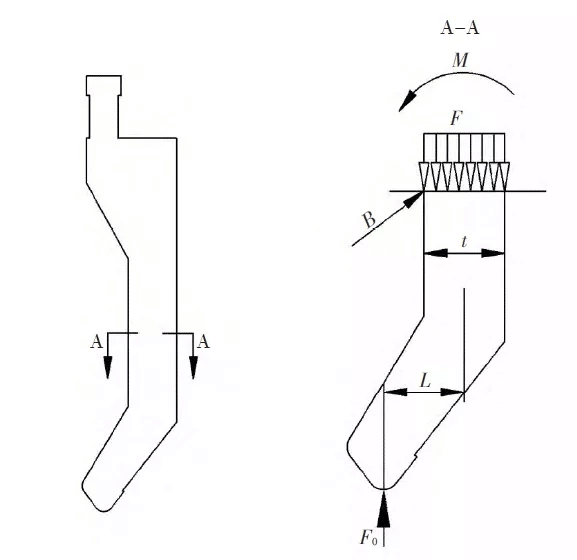
5. Analyse d'intensité
L'analyse de résistance de la partie col de cygne du moule est réalisée. Outre la pression exercée par la cintreuse, le moule est soumis au moment de flexion induit par la pression exercée dans la partie col de cygne. Sélectionnez la section AA du col de cygne pour l'analyse de résistance et calculez l'équation de colonne : analyse de résistance de la partie col de cygne du moule. Outre la pression exercée par la cintreuse, le moule est également soumis à la pression exercée dans la partie col de cygne. Le moment de flexion. Comme le montre la figure 4, l'analyse de l'état de contrainte AA de la section dangereuse du col de cygne montre que la largeur de la section est t, la distance verticale entre le centre de pression de la cintreuse et le centre de gravité de la section AA est L, la pression exercée par la cintreuse sur la matrice est F, la force F0 de réaction de la pièce sur la matrice, le moment de flexion de la section est M et il existe un risque de rupture au point B de la section. Après analyse, un diagramme simplifié de l'état de force de la section représentée sur la Fig. 4 AA est dessiné.
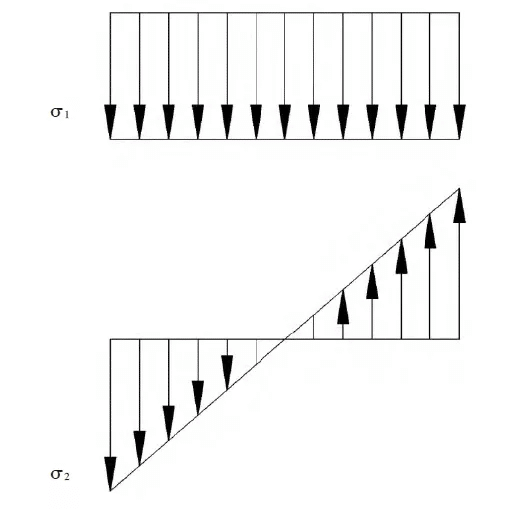

σ1——contrainte générée par la force externe F0
σ2——la contrainte générée par le moment de flexion
Dans l'équation (5), W est le coefficient de flexion de la section. La section AA étant un rectangle de hauteur t et de longueur h, w = t²h/6.
À partir de la formule (2), M=F0×L, et remplacez W et M dans la formule :
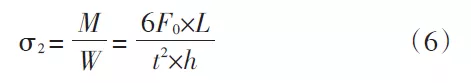
t——l'épaisseur de la section A, mm
L——la distance verticale entre le centre de pression de la cintreuse et le centroïde de la section A, en mm
h——la longueur de la matrice de pliage, mm
En remplaçant les valeurs σ1 et σ2 dans l'équation (3), on obtient σ3 sous la forme :
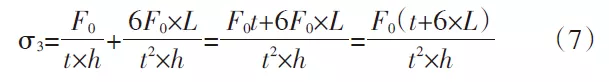
σ3 — la somme du moment de flexion et de la contrainte générée par M et la force externe F0
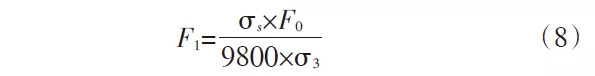
F1——Contrainte maximale pouvant être supportée par la section dangereuse AA du moule
δs — la limite d'élasticité du matériau en mode de flexion
En substituant le résultat σ3 de la formule (7) dans la formule (8) pour obtenir F1
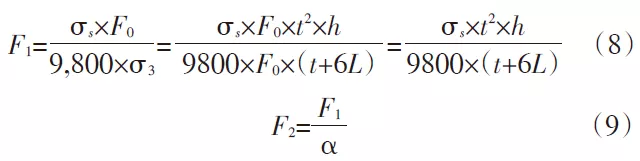
Dans la formule (9), α est le facteur de sécurité, généralement compris entre 1,1 et 1,2. Dans ce calcul, α = 1,15 est pris en compte, et les valeurs α et F1 sont substituées dans la formule (9) :
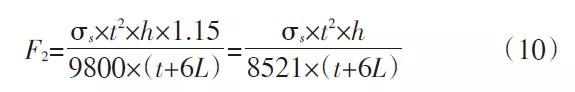
δs = 450 MPa, h = 2 530 mm, t = 50 mm, L = 27,5 mm. Dans la formule (10), la valeur F2 est de 1 553 t, ce qui signifie que la section AA conçue avec une force de flexion importante peut supporter une contrainte de 1 553 t. Cette valeur est bien supérieure à la force de flexion nécessaire au formage de la pièce, ce qui permet de répondre aux exigences de formage de la pièce.
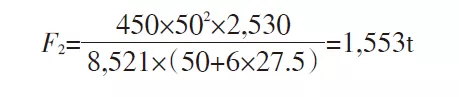
6. Optimisation structurelle
Selon les résultats du calcul ci-dessus, la contrainte de la section dangereuse AA est de 15 530 kN, ce qui est bien supérieur à la force de flexion de la pièce formant 5 930 kN, ce qui peut répondre aux exigences de moulage de la pièce.
Cependant, afin de réduire davantage l'intensité de travail de l'opérateur et de réduire le coût de fabrication du moule, il est nécessaire d'optimiser la conception du moule afin qu'il puisse satisfaire la réalisation du produit, réduire le
l'intensité du travail de l'opérateur et réduire le coût de fabrication du moule.
Selon la formule (10), la contrainte subie par la section dangereuse AA est liée à la limite d'élasticité σs du matériau du moule, à l'épaisseur t de la section A, à la longueur h du mode de pliage et à la distance verticale L entre le centre de pression de la cintreuse et le barycentre de la section A. Le matériau du moule étant généralement inchangé, σs est une valeur fixe ; la longueur de la pièce étant de 2 530 mm, elle aussi une valeur fixe L = t/2+2,5 ; la seule variable de la formule est donc t, et sa valeur est progressivement optimisée :
Recalculez en changeant la valeur de t de 50 à 30 :

Recalculez la valeur de t de 30 à 25 pour le recalcul :
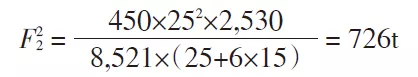
Recalculez en changeant la valeur de t de 25 à 20 :
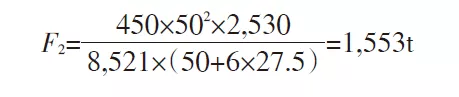
D'après les calculs ci-dessus, F32 est inférieur à la force de flexion maximale de la pièce formée, tandis que F12 et F22 sont supérieurs à cette force. Cependant, le coût de fabrication du moule est faible, ce qui facilite le montage et le démontage du moule. Il a donc été déterminé que la section dangereuse AA du moule avait une largeur de 25 mm. L'épaisseur de la partie active du reste du moule est de 25 mm. La courbure du col de cygne est excessivement courbée afin d'éviter toute concentration locale de contraintes. La taille de l'interface entre le moule et l'équipement peut être conçue en fonction du mécanisme de serrage de l'équipement.
7. Vérification des effets
La pratique a prouvé que le moule peut résister aux contraintes de la pièce pliée, et que sa rigidité et sa résistance répondent aux besoins réels de production. Afin de s'adapter aux exigences actuelles de la fabrication de pièces à haut rendement, à faible coût et à un rythme soutenu, la conception du moule, en tant que source de coûts, constitue un élément important du coût des pièces. La formule et le processus de calcul peuvent être appliqués à la conception du moule à col de cygne.
8. Conclusion
La section dangereuse de la matrice de cintrage à col de cygne est la plus éloignée du centre de pression. Selon le matériau et la structure du moule, la résistance de la section dangereuse est proportionnelle à son épaisseur.





















