Dans cet article, j'explorerai les Calcul de l'angle de courbure L'outil de pliage à grand arc est un aspect crucial du travail des métaux et de la fabrication. Comprendre le calcul précis des angles de pliage est essentiel pour obtenir des résultats précis et efficaces sur nos projets. Avec les méthodes et les outils appropriés, nous pouvons améliorer notre flux de travail et garantir que nos pliages répondent aux spécifications requises. Je vous présente les techniques et les considérations qui vous aideront à maîtriser ce calcul important et, à terme, à améliorer la qualité de votre travail.

Comprendre les angles de flexion

Angles de flexion sont fondamentaux pour déterminer le comportement des matériaux sous contrainte. Pour le pliage de grands arcs, le calcul devient encore plus crucial en raison de la taille et de la complexité des outils utilisés. Des calculs précis permettent d'éviter le gaspillage de matière et de garantir l'intégrité structurelle.

Les angles de pliage sont fondamentaux pour déterminer le comportement des matériaux sous contrainte. Pour le pliage de grands arcs, le calcul devient encore plus crucial en raison de la taille et de la complexité des outils utilisés. Des calculs précis permettent d'éviter le gaspillage de matière et de garantir l'intégrité structurelle.

Pourquoi le calcul de l’angle de courbure est-il important ?

La précision des calculs d'angle de pliage influence directement la qualité du produit fini. Un pliage incorrect peut entraîner des erreurs coûteuses, comme un mauvais alignement des pièces, des imprécisions dimensionnelles et une augmentation des déchets. Un calcul correct avant le début du processus de pliage permet de réduire les erreurs et de garantir que le pliage est conforme aux spécifications requises.

Première méthode-Calcul de l'angle de courbure

Épaisseur de la plaque : 2 mm, angle de pliage : 120 degrés, rayon extérieur : 30, rayon de la couche neutre : 29, pliage en arc. Nous calculons la longueur de l'arc de la couche neutre. Par conséquent, le nombre de couteaux de pliage et l'angle de pliage de chaque couteau sont également égaux à la moitié de l'épaisseur de la couche neutre multipliée par la longueur de celle-ci.

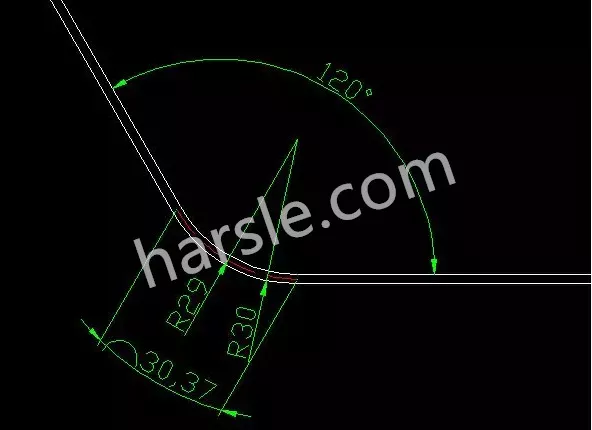
Dans l'image ci-dessus, combien de couteaux doivent être pliés pour le pliage en arc et quel est l'angle de pliage de chaque couteau ?

Si nous obtenons 2 mm par couteau.

Nombre de couteaux de pliage = longueur de l'arc / 2 mm = 30,37 / 2 = 15

Nombre de couteaux de pliage 15

Angle de courbure = 180- {(2/longueur de l'arc) X (180-angle de courbure)}=180-{(2/30,37)X60}=176

176 degrés par angle de pliage du couteau

Si nous n'avons pas de longueur d'arc lors du pliage, nous pouvons également calculer selon la formule suivante.

Angle de courbure = 180-{(2/3,14X rayon neutre) X180}=180-{(2/3,14X29)X180}=176

Si vous souhaitez saisir 3 mm par couteau, remplacez 2 dans la formule ci-dessus par 3.

Bien entendu, la formule ci-dessus est une formule de calcul théorique. Lors du traitement réel, les résultats calculés selon cette formule sont ajustés.

Deuxième méthode-Calcul de l'angle de courbure

Comment plier l'arc quand il n'y a pas de moule ?

Comme le montre la figure ci-dessus, l'épaisseur de la plaque est T = 2 mm et l'angle central est de 90°.

⒈Calculez d'abord la longueur de l'arc : longueur de l'arc L = 90 ° * 3,14 ÷ 180 ° * couche centrale R59 = 92,63

⒉Sélectionnez la matrice de pliage : la matrice supérieure avec une épée droite, la matrice inférieure avec 8v.

⒊Calculer l'avance par pli : avance par pli = la moitié de la largeur V de la matrice sélectionnée.

⒋Calculez le nombre de plis : le nombre de plis doit être = longueur de l'arc L92,63 ÷ largeur V moitié 4 mm = 23 plis.

⒌Calculez la taille de positionnement de chaque pli : la taille de positionnement du premier pli est calculée et l'autre est réduite de 4 mm par pli.

⒍Calculez enfin l'angle de chaque courbure : calculez la formule en fonction d'une certaine algèbre du triangle.

⒎Après les calculs ci-dessus, le matériau de la feuille usagée est utilisé pour un pliage d'essai et le produit est traité une fois l'angle essayé.

Conclusion

Maîtriser le calcul de l'angle de cintrage des grands arcs de cercle améliore non seulement l'efficacité, mais aussi la qualité globale du produit final. En comprenant les facteurs impliqués et en utilisant les bons outils, vous pouvez obtenir des pliages précis qui répondent aux exigences de votre projet. Alors que nous perfectionnons continuellement nos techniques, l'importance de calculs précis est primordiale.