عند العمل على المشاريع، يُعدّ فهم أهمية تحديد الطول الفعلي للمكون أمرًا بالغ الأهمية. تضمن القياسات الدقيقة توافق المكونات معًا بشكل مثالي وعملها على النحو المطلوب. في هذه المقالة، سأشارك أساليب ونصائح عملية وجدتها فعّالة لتحديد الطول الفعلي لمختلف المكونات. سواء كنت تعمل في مجال التصنيع أو مشاريع "اصنعها بنفسك"، فإن إتقان هذه المهارة يُحسّن دقتك وكفاءتك بشكل كبير. دعونا نتعمق في أفضل الممارسات لتحقيق قياسات دقيقة!

في معالجة صفائح معدنية غالبًا ما نصادف قطعًا من مختلف الأشكال، مثل أنابيب التهوية، والمفاصل المشوهة، وما إلى ذلك. لإكمال معالجتها، يجب أولًا فرد الصفائح المعدنية، ثم فرد سطح الجسم على سطح مستوٍ وفقًا لشكله وحجمه الفعليين. يُعد فرد الصفائح المعدنية عملية تحضيرية لـ صفائح معدنية مادة، وهي أيضًا شرط أساسي للمعالجة الصحيحة لأجزاء الصفائح المعدنية. لرسم مخطط طيّ الصفائح المعدنية بشكل صحيح، من الضروري معرفة الأبعاد الفعلية لمخطط الطيّ أو الأبعاد الفعلية لمكوناته ذات الصلة. عندما لا يكون السطح ثلاثي الأبعاد للخط وسطح الإسقاط متوازيين، فإن رسومات التصميم في الإسقاط لا تنعكس بطولها الحقيقي، لذلك يجب استخدام طريقة بيانية قبل الطيّ لمعرفة الطول الحقيقي لقطعة الخط.

تشمل طرق إيجاد الطول الحقيقي لقطعة مستقيمة طريقة الدوران، وطريقة المثلث القائم، وطريقة شبه المنحرف القائم، وطريقة مستوى الإسقاط المساعد. يُعدّ إتقان وتطبيق هذه الطرق لإيجاد الطول الحقيقي لقطعة مستقيمة شرطًا أساسيًا وأساسًا لاكتساب مهارات طيّ الصفائح المعدنية.

طريقة الدوران

تتضمن طريقة الدوران تدوير خط مائل حول محور عمودي على مستوى إسقاط إلى موضع موازٍ لمستوى إسقاط آخر، بحيث يكون طول قطعة الخط المسقط على هذا المستوى هو الطول الحقيقي للخط المائل. لتسهيل الرسم، يمر المحور عادةً فوق إحدى نهايتي الخط المائل، وتكون نقطة النهاية مركز الدائرة، ويكون الخط المائل نصف قطر الدوران.

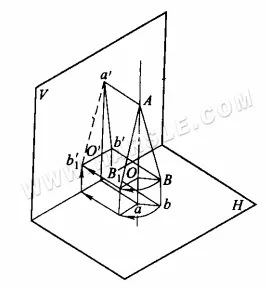
مبدأ الدوران للطول الحقيقي: يوضح الرسم البياني أدناه مبدأ الدوران للطول الحقيقي. ab هو خط موضع عام، يميل على أي مستوى إسقاط. إسقاطا ab، a'b'، على المستوى V وإسقاط ab على المستوى H أقصر من الطول الحقيقي. بافتراض أن المحور AO عمودي على المستوى H عند أحد طرفي AB، فعندما يدور AB حول المحور AO إلى الوضع AB1 الموازي للمستوى V، فإن إسقاطه a'b1′ على المستوى V (يشير الخط المتقطع في الرسم البياني إلى الطول الحقيقي) سيعكس طوله الحقيقي.

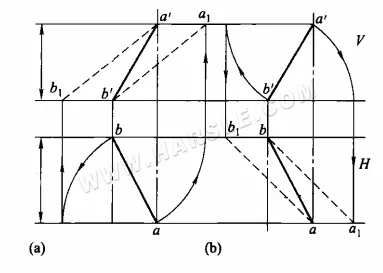
طريقة الدوران للأطوال الحقيقية: يوضح الرسم البياني أدناه الطريقة المحددة لاستخدام طريقة الدوران للأطوال الحقيقية. في الرسم البياني أدناه (أ)، يُدار الإسقاط الأفقي ab بحيث يوازي الإسقاط المتعامد، مما ينتج عنه النقطتان a1 وb1، اللتان تصلان a1b' أو a'b1، وهو الطول الحقيقي للقطعة المستقيمة AB. في الرسم البياني أدناه (ب)، يُدار الإسقاط المتعامد a'b' بحيث يوازي الإسقاط الأفقي، مما ينتج عنه a1 وb1، ويصلان a1b أو ab1، وهو الطول الحقيقي للقطعة المستقيمة AB.

مثال: يُظهر الرسم البياني أدناه رسمًا تخطيطيًا للطول الحقيقي لمنشور مائل باستخدام طريقة الدوران. كما يتضح من الإسقاط، فإن قاعدة المنشور المائل موازية للمستوى الأفقي، ويعكس إسقاطه الأفقي شكله المصمت وطوله الحقيقي. الأوجه الأربعة المتبقية (الأضلاع) هي مجموعتان من المثلثات، لا تعكس إسقاطاتها الشكل الحقيقي. للحصول على الشكل الحقيقي لمجموعتي المثلثات، يجب إيجاد الطول الحقيقي لمنشوريهما. ولأن الشكل متماثل من الأمام إلى الخلف، فإن الطول الحقيقي للمنشورين الجانبيين فقط هو المطلوب لرسم الرسم البياني.

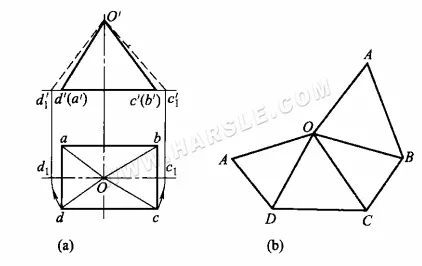
الخطوات المحددة في رسم مخطط تفصيلي هي

١. استخدم طريقة الدوران لإيجاد الأطوال الحقيقية للأضلاع الجانبية Oc وOd. كما هو موضح في الرسم البياني أدناه، افترض أن O مركز الدائرة، وأن Oc وOd نصف قطر الدوران، ثم اقطع الخط الأفقي في c1 وd1. c1 وd1 من c1 وd1 لأعلى الخط الرأسي، وخط الامتداد الإسقاطي المتعامد c'd' المتقاطع في c1'd1′، والواصل بين O'c1′ وO'd1′ هو الطول الحقيقي للمنشور الجانبي Oc وOd.

٢. ارسم خطًا AD بطول يساوي ad في الموضع المناسب على الرسم التخطيطي، ثم ارسم △AOD بحيث يكون A وD مركزي الدائرة، وOd' نصف قطر القوس، ويتقاطع عند O؛ ثم ارسم قوسًا بحيث يكون O مركز الدائرة، وOc1′ نصف قطره، ويتقاطع مع القوس المرسوم بحيث يكون D مركزه، وdc نصف قطره عند C. وصّل OC وDC للحصول على △DOC. ارسم الضلعين المتبقيين من △COB و△BOA بنفس الطريقة للحصول على مخروط مثلثي ذي ضلعين ممتدين.

الشكل أدناه هو مخروط مقطوع، الطول الحقيقي للمخروط والتوسع، يجب عليك أولاً رسم الجزء العلوي من المخروط، ليصبح مخروطًا كاملاً، ثم قم بعمل سلسلة من سطح المخروط، واستخدم طريقة الدوران للعثور على هذه الخطوط التي تم قطع جزء منها من الطول الحقيقي للخط (متاح أيضًا لترك جزء من الطول الحقيقي للخط)، يمكنك عمل توسع للشكل.

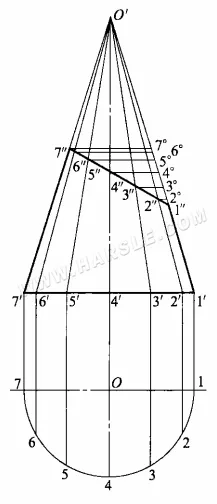
للعثور على الطول الحقيقي للجزء المقطوع من الخط، تكون خطوات الرسم التخطيطي كما يلي.

1. قم بتمديد خط الشكل 1'1″ و7'7″ ليتقاطعا، مما يؤدي إلى الجزء العلوي من المخروط O'.

2. اصنع دائرة قاعدة المخروط، وقسم محيط دائرة القاعدة إلى عدد من الأجزاء المتساوية (هنا 1/2 محيط دائرة القاعدة مقسم إلى 6 أجزاء متساوية)، للحصول على أجزاء متساوية 1، 2، …، 7، من كل نقطة متساوية إلى المنظر الرئيسي للرصاص الرأسي، وتقاطع الإسقاط المتعامد لدائرة القاعدة عند نقاط 1′، 2′، …، 7′، ثم من كل نقطة وأعلى المخروط O 'للخط، للحصول على خطوط سطح المخروط.

٣. من بين خطوط المخروط، فقط خطا الحدود الخارجية ١″١′ و٧″٧′ هما الموازيان للإسقاط المتعامد ويعكسان طوله، بينما لا تعكس بقية الخطوط الطول الحقيقي. الطريقة هي رسم خط موازٍ بطول ٧″١′ من ٧″، ٦″…، ٢″، ويتقاطع مع خط الكنتور O'١′ عند ٧°، ٦″…، ٢°، O'٦°، O'٥°،…، O'٢°، بحيث يكون طولهما الحقيقي ٢″.

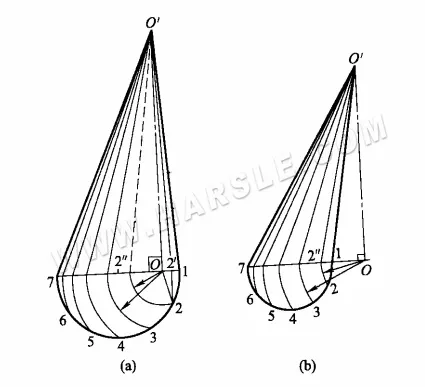
يوضح الرسم البياني أعلاه الطول الحقيقي للمخروط المائل عند الدوران. والخطوات كالتالي:

1. أولاً قم بعمل نصف دائرة القاعدة، ثم قم بتقسيم محيط الدائرة الأساسية إلى عدد من الأجزاء المتساوية (في الرسم البياني إلى 6 أجزاء متساوية).

2. مع القاعدة العمودية O كمركز للدائرة، O1، O2، …، O6 لنصف قطر القوس، وتقاطع الخطوط 1 ~ 7 عند 2 "وهكذا في كل نقطة.

٣. ارسم خطًا مستقيمًا من النقطتين ٢ بوصة، إلخ، إلى O'، وO'٢'، إلخ، حيث يمثل هذا الخط الطول الحقيقي للخط المار بالاعتدالين. بمعنى آخر، O'٢' هو الإسقاط العمودي لخط O2، وO'٢″ هو الطول الحقيقي لخط O2.

يوضح الرسم البياني أدناه الأطوال الحقيقية لمنشورات المفصل المربع باستخدام طريقة الدوران وتوسيعها.

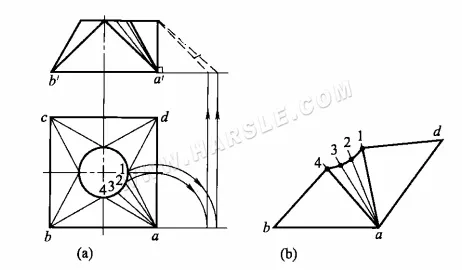
الخطوات اللازمة لرسم الأطوال الحقيقية للمنشورات هي

1. ارسم المنظر الرئيسي والمنظر العلوي، ثم قم بمساواة فتحة دائرة المنظر العلوي وتوصيل الخطوط العادية المقابلة.

2. قم بتدوير الخطوط العادية a1، (a4)، a2، (a3) وارسم خطوطًا رأسية لأعلى لاستخلاص أطوالها الحقيقية a-1، (a-4) وa-2، (a-3) على الجانب الأيمن من العرض الرئيسي.

3. باستخدام أطوال الخطوط العادية الحقيقية، وأطوال حافة الفم المربعة وأطوال انتشار القوس المكافئة للفم الدائري، ارسم انتشارات 1/4 بالتناوب.

عندما يكون الجزء الانتقالي من الأنبوب المربع مقابل الأنبوب الدائري، يجب أن يكون هناك وصلة مربعة دائرية. يمكن أن تكون فوهة المربع إما مربعة أو مستطيلة، ويمكن أن تكون الفوهة الدائرية في المنتصف أو على أحد الجانبين أو في إحدى الزوايا. وبالتالي، يمكن تعديل شكل هذه الوصلات، ولكن طريقة تحديد الطول الحقيقي للوصلات المربعة والدائرية هي نفسها تقريبًا.

طريقة المثلث القائم

طريقة المثلث القائم هي طريقة شائعة الاستخدام لإيجاد الطول الحقيقي.

مبدأ طريقة المثلث القائم الزاوية وطريقة الرسم: الرسم التخطيطي التالي (أ) هو الرسم التخطيطي الأساسي لطريقة المثلث القائم الزاوية للطول الحقيقي. القطعة المستقيمة AB ليست موازية لمستوى الإسقاط، وإسقاطها ab وa'b' لا يعكسان الطول الحقيقي. في المستوى ABba، يُرسم خط موازٍ لـ ab عبر النقطة A ويتقاطع مع Bb في النقطة B1، مما يعطي المثلث القائم الزاوية ABB1. في هذا المثلث، يمكن إيجاد الطول الحقيقي للوتر AB في المثلث القائم الزاوية بمعرفة طولي الضلعين القائمين AB1 وBB1. ويوجد طولا AB1 وBB1 على الرسم التخطيطي للإسقاط على النحو التالي AB1 = ab أو BB1 = b'b1′ أو BB1 = b'bx – a'ax. إن معرفة هذين الضلعين القائمين الزاوية يرسم المثلث القائم الزاوية المطلوب بشكل فريد.

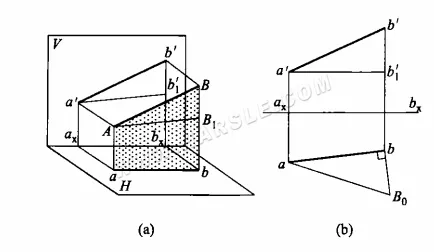
يوضح الشكل (ب) أعلاه استخدام طريقة المثلث القائم لإيجاد الطول الحقيقي. يُعرف إسقاط خط AB باسم ab وa'b'. لإيجاد الطول الحقيقي لخط AB، يمكنك أولًا رسم خط أفقي يمر بالنقطة a'، ويتقاطع مع الخط bb' في النقطة b1′، bb1′، أي طول ضلع قائم الزاوية. ثم، المنظر العلوي لـ ab لحافة قائمة أخرى، فوق الخط الرأسي المشار إليه في النقطة b، ويتقاطع مع النقطة bB0 = b'b1′، متصلًا بـ aB0، أي الطول الحقيقي للقطعة المستقيمة.

مثال: يوضح الرسم البياني أدناه مفصل فم مربع صغير وآخر كبير، حاول إيجاد الطول الحقيقي لخطه الرئيسي AC وخطه المساعد BC.

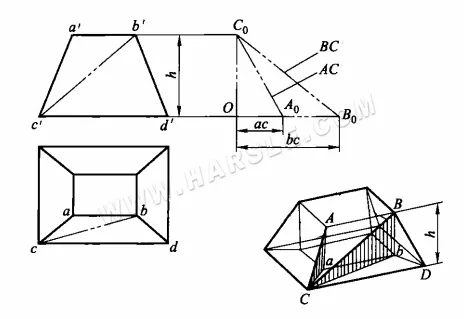
يتضح من الرسم التخطيطي أن الطول الحقيقي AC يُوجد في مثلث قائم الزاوية، حيث يكون الضلعان القائمان aC وAa، بينما يُوجد الطول الحقيقي BC في المثلث القائم الزاوية BbC. في كلا المثلثين، Aa = Bb = h، وهو ما يساوي ارتفاع المفصل. الضلعان القائمان الآخران aC وbC يساويان إسقاطي AC وBC في المنظر العلوي على التوالي. بهذه الطريقة، يمكن إيجاد الطول الحقيقي لـ AC وBC كما يلي.

1. اصنع زاوية قائمة B0OC0.

2. اعترض OA0 وOB0 على الجانب الأفقي لتلك الزاوية القائمة التي تساوي ac وbc على التوالي في المنظر العلوي، واعترض OC0 على الجانب الرأسي الذي يساوي الارتفاع h في المنظر الرئيسي.

3. قم بتوصيل C0A0 وC0B0، ثم يكون الوتر C0A0 وC0B0 هما الطولان الحقيقيان للطولين AC وBC المطلوبين.

طريقة شبه المنحرف القائم الزاوية

تعتبر طريقة شبه المنحرف ذو الزاوية القائمة أيضًا طريقة شائعة لإيجاد الأطوال الحقيقية.

مبدأ طريقة شبه المنحرف القائم الزاوية لحساب الطول الحقيقي وطريقة الرسم: يوضح الرسم التخطيطي التالي مبدأ استخدام طريقة شبه المنحرف القائم الزاوية لحساب الطول الحقيقي. لا يعكس الموقع العام للمستقيم AB على السطح V والسطح H الطول الحقيقي، ولكن يمكن الحصول على نقطتي طرفي المستقيم AB والمسافة بين السطح V على السطح H، أي Aa وBb، وكذلك على السطح V، أي Aa 'وBb. بناءً على هذا المبدأ، يمكن إيجاد الطول الحقيقي للمستقيم AB باستخدام طريقة شبه المنحرف القائم الزاوية. هناك طريقتان محددتان لرسم الأطوال الحقيقية بيانيًا.

1. باستخدام الإسقاط المتعامد للطول الحقيقي للخط AB: الإسقاط المتعامد لـ AB a'b' باعتباره الحافة السفلية لشبه المنحرف القائم الزاوية، من a'، b' نقطتين على التوالي لأعلى الخط العمودي، يقطع طول Aa'، Bb'، المتصل بـ AB، أي للمطلوب.

2. هو استخدام الإسقاط الأفقي للطول الحقيقي للقطعة المستقيمة AB: الإسقاط الأفقي لـ AB كحافة سفلية لشبه منحرف قائم الزاوية، من a، b نقطتين على التوالي لأعلى الخط العمودي، يقطع طول Aa، Bb، يربط AB وهو المطلوب.

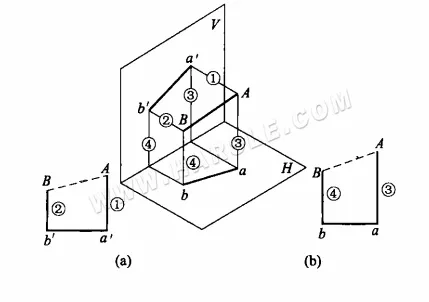
مثال: يوضح الشكل التالي مفصل تشوه حدوة الحصان، فمه العلوي والسفلي عبارة عن دوائر، لكن الدائرتين ليستا متوازيتين وليستا متساويتين في القطر، حاول عمل طريقة شبه منحرف بزاوية قائمة لطول خطه ومخطط التوسع.

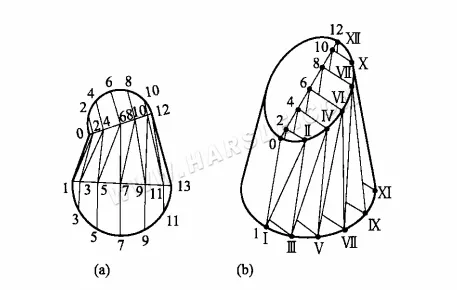
يتضح من الشكل (أ) أعلاه، لأن سطحه ليس مخروطيًا، ولرسم مخطط تمدده، يكفي استخدام الخط الواصل بين السطح وعدد من المثلثات، واحدًا تلو الآخر، لإيجاد الشكل الحقيقي لهذه المثلثات. فيما يلي خطوات الرسم البياني التفصيلية.

1. اصنع 12 جزءًا متساويًا من الفم العلوي والسفلي، وقسم السطح إلى 24 مثلثًا كما هو موضح في الرسم التخطيطي.

2. أوجد الأطوال الحقيقية للخطوط 1-2، 2-3، …، 2-VII، ثم ارسم الشكل الحقيقي لسلسلة المثلثات.

في مثل هذه الأمثلة، إذا استُخدمت طريقة الدوران أو طريقة المثلث القائم لإيجاد الطول الحقيقي، فيجب إسقاط القطعة المستقيمة في المنظر العلوي. وبما أن السطح العلوي لمفصل تشوه حدوة الحصان ومستوى الإسقاط الأفقي مائلان، فإن السطح العلوي في المنظر العلوي ينعكس على شكل قطع ناقص. ومن الواضح أن هاتين الطريقتين لتوسيع الخريطة أكثر صعوبة، لذا يُنصح حاليًا باستخدام طريقة شبه المنحرف قائم الزاوية.

كما في الشكل (ب) أعلاه، يمتد امتداد السطح المطوي Ⅰ-1-Ⅱ-2-Ⅲ-3…XII-12 إلى الشكل الموضح أدناه، ثم الشكل فوق خط الطي Ⅰ-Ⅱ-Ⅲ…XII، أي الطول الحقيقي Ⅰ-Ⅱ، Ⅱ-Ⅲ، …، Ⅵ-VII، وهكذا. هذه الطريقة لإيجاد الأطوال الحقيقية هي طريقة شبه المنحرف قائم الزاوية.

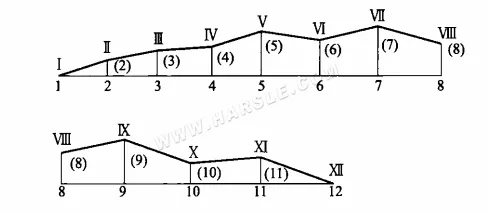
كما يتضح من طريقة الرسم البياني، تعتمد طريقة شبه المنحرف القائم الزاوية أيضًا على إسقاط خط مائل كقاعدة، بحيث تكون المسافة بين طرفي الخط المائل من نفس مستوى إسقاط الضلعين القائمين. بعد تشكيل شبه منحرف قائم الزاوية، يُحسب وتر شبه المنحرف القائم الزاوية، أي الطول الحقيقي للخط المطلوب. ويُعتبر المثلث القائم الزاوية حالة خاصة من طريقة شبه المنحرف القائم الزاوية، حيث يكون طول الضلع القائم الزاوية صفرًا.

تُستخدم الطريقة المذكورة أعلاه للحصول على خطي جانبي كل مثلث على سطح مفصل تشوه حدوة الحصان، ويكون الجانب الآخر منه طول الفتحتين الدائريتين العلوية والسفلية مساويًا للقوس غير المطوي. بهذه الطريقة، يمكن إنشاء سلسلة من المثلثات بطريقة المثلثات ذات الأضلاع الثلاثة المعروفة، والتي تُرتّب للحصول على الرسم التخطيطي التالي لمفصل تشوه حدوة الحصان.

طريقة تغيير الوجه

بالإضافة إلى الطرق المذكورة أعلاه للعثور على الطول الحقيقي للخط، هناك أيضًا الطريقة الشائعة لتغيير السطح.

مبدأ طريقة تغيير السطح للطول الحقيقي وطريقة الرسم: يتمثل مبدأ طريقة تغيير السطح في الحفاظ على القطعة الفضائية دون تغيير، ثم إنشاء سطح إسقاط جديد لجعلها موازية للقطعة المطلوبة وعمودية على القطعة الأصلية. سيعكس إسقاط القطعة على سطح الإسقاط الجديد طولها الحقيقي. يوضح الرسم البياني أعلاه مخططًا تخطيطيًا للطول الحقيقي لقطعة مستقيمة.

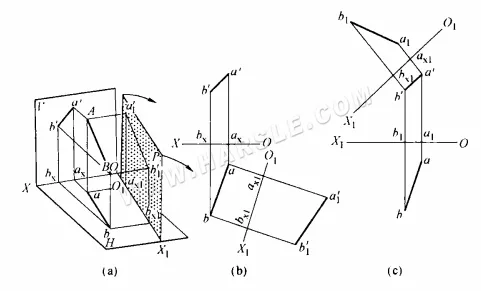
كما يتضح من الرسم البياني أعلاه (أ)، فإن القطعة المستقيمة AB ليست موازية لكلا مستويي الإسقاط H وV، ولا يعكس إسقاطها الطول الحقيقي. يعكس الإسقاط الجديد a1'b1′ الطول الحقيقي لـ AB. يكشف التحليل الإضافي للمساحة الموضحة في الشكل (أ) أعلاه عن علاقات الإسقاط التالية لطريقة تغير السطح.

1. بما أن سطح الإسقاط الجديد P موازي لـ AB وعمودي على المستوى H، فإن خط التقاطع بين سطح الإسقاط الجديد P والمستوى H، O1X1 (يسمى محور الإسقاط الجديد)، يكون بالضرورة موازيًا لإسقاط المستوى H ab للخط AB، O1X1 // ab، كما ينعكس في إسقاط المستوى H.

2. بما أن سطحي P و V عموديان على سطح H في نفس الوقت، فإن المسافة من الإسقاط a1'b1′ لسطح P إلى O1X1 والمسافة من الإسقاط a'b' لسطح V إلى OX يجب أن تعكس في نفس الوقت المسافات العمودية من نقطتي النهاية A و B للخط المكاني إلى سطح H، وهما متساويتان، a1ax1 = a'ax = Aa و b1'bx1 = Bb. لتسهيل التحديد، فإن الإسقاط الجديد الموازي لـ AB يسمى الإسقاط a1'b1′ الذي يعكس الطول الحقيقي الإسقاط الجديد، والإسقاط a'b' الذي لم يعكس الطول الحقيقي في الأصل يسمى الإسقاط القديم أو البديل، ويسمى إسقاط المستوى H العمودي عليهما في نفس الوقت الإسقاط الثابت. وبهذه الطريقة، يمكن التعبير عن علاقة الإسقاط لطريقة سطح الاستبدال على أنها المسافة من الإسقاط الجديد إلى المحور الجديد تساوي المسافة من الإسقاط القديم إلى المحور القديم.

3. بما أن كل من سطحي P وV عموديان على سطح H، فإن الاتصال بين الإسقاط P والإسقاط H عند أي نقطة على الخط يجب أن يكون عموديًا على محور الإسقاط الجديد O1X1، ويكون الخط بين الإسقاط الثابت والإسقاطين القديم والجديد عموديًا على محوري الإسقاط القديم والجديد على التوالي، بعد الفتح.

وفقًا لعلاقة الإسقاط المذكورة أعلاه لطريقة التبديل، يجب أن تكون خطوات الرسم البياني

1. كما هو موضح في (ب) أعلاه، اجعل محور الإسقاط الجديد O1X1 موازيًا لـ ab.

2. ارسم خطًا عموديًا يمر عبر النقطتين a وb إلى المحور O1X1 ويتقاطع مع المحور O1X1 عند النقطتين ax1 وbx1.

3. انقل الإسقاطين a' وb' للمستوى V إلى المحور OX إلى المستوى الإسقاطي الجديد، وقم بقياس ax1a1'=axa' وbx1b1'=bxb' على الخطوط الرأسية.

4. قم بتوصيل النقطتين a1′ وb1′، الإسقاط الجديد a1’b1′ لخط AB، والذي يعكس الطول الحقيقي لـ AB.

مثال: يوضح الرسم البياني أدناه استخدام طريقة المستوى الإسقاطي المساعد لإيجاد الشكل الحقيقي للمقطع الأسطواني.

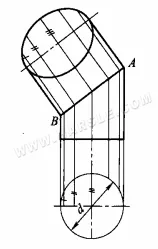
الخطوات في الرسم هي كما يلي.

1. اصنع منظرًا رئيسيًا وعلويًا، وقسم المنظر العلوي على نصف محيط الدائرة إلى 6 أجزاء متساوية.

2. ارسم خطًا رأسيًا لأعلى عبر النقطة المتساوية البعد لتحديد موضع الخط الرئيسي في العرض الرئيسي.

3. رسم خطوط عمودية إلى الأسفل من النقاط المتساوية البعد لتتقاطع مع خط المنتصف السفلي، والعرض بين الخطوط المستقيمة للقسم

4. رسم خطوط عمودية من خلال تقاطع الخطوط على الفتحة المائلة للقسم إلى المحور الطويل الموازي للفتحة المائلة للقسم، ثم رسم المسافة بين النقاط المتساوية البعد في المنظر العلوي والخط المركزي للدائرة السفلية، بدورها، إلى النقاط في المنظر الثانوي، وفقًا لقاعدة "العرض المتساوي".

5. قم بتوصيل النقاط من أجل إنشاء قطع ناقص متصل للقسم.

يوضح الرسم البياني أدناه استخدام طريقة مستوى الإسقاط المساعد لإيجاد الشكل الحقيقي لمقطع المخروط المستقيم. تشير الأشكال 1، 2، ... (7) إلى ترتيب رسم وتوصيل الخطوط.

بشكل عام، ليس من الضروري رسم خطوط على سطح المخروط لرسم الشكل الحقيقي للمقطع المخروطي، بل يُفضل استخدام طريقة دائرة اللحمة، كما هو موضح في الشكل أعلاه. لتوضيح الخطوط، سيتم رسم خطوات الرسم التخطيطي الثلاث بشكل منفصل في هذا المثال، دون الحاجة إلى فصل الرسم التخطيطي الفعلي. الخطوات كالتالي:

1. دوائر اللحمة: يقسم خط إسقاط المقطع إلى 6 أجزاء متساوية؛ يتقاطع الخط الأفقي للنقاط المتساوية أعلاه مع خط الكنتور؛ يرسم الخط الرأسي إلى الأسفل من كل نقطة تقاطع على خط الكنتور ويتقاطع في أسفل المخروط؛ ترسم دوائر اللحمة بدورها مع مركز الدائرة O، انظر الشكل (أ) أعلاه.

2. المنظر العلوي للمقطع العرضي: عن طريق رسم خط عمودي لأسفل عبر كل تداخل لخطوط المقطع العرضي في المنظر الرئيسي، متقاطعًا مع دائرة خط العرض المقابلة، يتم الحصول على سلسلة من نقاط التقاطع؛ عن طريق ربط نقاط التقاطع، يمكن الحصول على إسقاط المنظر العلوي للمقطع العرضي، انظر الشكل (ب) أعلاه.

٣. لإيجاد الشكل الحقيقي للمقطع: ارسم قطعًا ناقصًا موازيًا للمحور الطويل للمقطع ١″٧″؛ ارسم خطوطًا عمودية من كل نقطة متساوية من المقطع ١″٧″ إلى المحور الطويل ١″٧″؛ ووفقًا لمبدأ تساوي العرض، ارسم سلسلة من العروض أ، ب، ج، د، وهـ للمقطع في المنظر العلوي على الإسقاط المساعد، بحيث تكون النقاط ٢″، ٣″، ٤″، ٥″، و٦″؛ وصّل النقاط، أي الشكل الحقيقي للمقطع المخروطي، انظر الشكل (ب) أعلاه. الشكل (ج) أعلاه.

يوضح الرسم البياني أدناه استخدام طريقة سطح الإسقاط المساعد لإيجاد الشكل الحقيقي للمقطع المخروطي المائل.

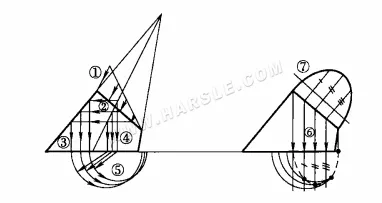
يُشبه استخدام المنظر المساعد للشكل الحقيقي للمقطع المخروطي المائل استخدام الشكل الحقيقي للمقطع المخروطي المتعامد. إلا أن المخروط المائل يتميز بميل قمته إلى جانب واحد وميل محوره أيضًا، مما يجعل مركز سلسلة دوائر اللحمة لا يقع في نفس النقطة على المحور نفسه. لذلك، بدلًا من عمل دوائر متحدة المركز، يُصنع مخروط بمركز واحد لكل دائرة لحمة. يمكن إتقان هذه الميزة باتباع الخطوات الثلاث الموضحة أعلاه لرسم المنظر المساعد لمقطع مصمت.

خطوات الرسم المحددة هي كما يلي.

1. بالنسبة لدائرة النسيج: خط القسم 4 أجزاء متساوية؛ بالنسبة للنقاط المتساوية من الخط الأفقي، تتقاطع مع خط الكنتور؛ من خط الكنتور على النقاط نزولاً إلى الخط الرأسي، تتقاطع مع الدائرة السفلية؛ النقاط المتساوية من الخط الأفقي وتقاطع محور النقاط لدائرة النسيج من المركز، مركز الدائرة إلى الدائرة السفلية؛ على التوالي، مركز دائرة النسيج ونصف القطر المقابل لدائرة النسيج.

2. المنظر العلوي للقسم: من خلال المنظر الرئيسي لخطوط القسم لكل التباس، والخطوط الرأسية المتجهة للأسفل، وتقاطع دائرة خطوط العرض المقابلة، مما يؤدي إلى سلسلة من نقاط التقاطع؛ إلى جانب نقاط التقاطع، يمكنك الحصول على المنظر العلوي لإسقاط القسم.

3. لإنشاء الشكل الحقيقي للقسم: وفقًا لعرض شكل القسم الموجود في المنظر العلوي، قم بعمل عرض مساعد 1/2 لرسم الشكل الحقيقي 1/2 للقسم المخروطي المائل.

مقارنة بين طرق الطول الحقيقي

وبناء على التحليل أعلاه، يمكن إجراء مقارنة بسيطة بين الطرق الأربع لإيجاد الطول الحقيقي لخط حقيقي.

تحل طريقة الدوران الطول الحقيقي عن طريق تغيير موضع الشكل في الفضاء، دون تغيير موضع مستوى الإسقاط.

تحل طريقة التبديل الطول الحقيقي عن طريق تغيير موضع المستوى الإسقاطي دون تغيير موضع الشكل.

تحل طريقة المثلث القائم وطريقة شبه المنحرف قائم الزاوية (يمكن اعتبار طريقة المثلث القائم كحالة خاصة لطريقة شبه المنحرف قائم الزاوية) خط الطول الحقيقي عن طريق عدم تغيير موضع الشكل الفضائي أو موضع مستوى الإسقاط.