При работе над проектами крайне важно понимать важность определения фактической длины компонента. Точные измерения гарантируют идеальную совместимость компонентов и их функциональность. В этой статье я поделюсь практическими методами и советами, которые я считаю эффективными для определения фактической длины различных компонентов. Независимо от того, занимаетесь ли вы производством или мастерите своими руками, овладение этим навыком может значительно повысить вашу точность и эффективность. Давайте рассмотрим лучшие методы достижения точных измерений!

При обработке листовой металл Часто встречаются детали, заготовки различной формы, такие как вентиляционные трубы, деформированные соединения и т.д. Для их обработки листовой металл необходимо предварительно развернуть, то есть разложить поверхность изделия на плоскости в соответствии с его фактической формой и размерами. Развертка листового металла является подготовительным процессом к обработке. листовой металл Материал, из которого изготавливаются детали, также является необходимым условием для правильной обработки листового металла. Для правильного построения развёртки листового металла необходимо знать фактические размеры развёртки или фактические размеры соответствующих её компонентов. Если трёхмерная поверхность линии и поверхность проекции не параллельны, проектный чертеж в проекции не отражает её действительную длину, поэтому перед развёрткой необходимо графическим способом определить действительную длину отрезка.

Методы определения действительной длины отрезка включают в себя метод вращения, метод прямоугольного треугольника, метод прямой трапеции и метод вспомогательной плоскости проекции. Освоение и применение этих методов определения действительной длины отрезка является предпосылкой и основой для приобретения навыков развёртки листового металла.

Метод вращения

Метод вращения заключается в повороте наклонной прямой вокруг оси, перпендикулярной плоскости проекции, до положения, параллельного другой плоскости проекции, при этом проецируемый отрезок на эту плоскость проекции представляет собой действительную длину наклонной прямой. Для удобства графического представления ось обычно проходит через одну из конечных точек наклонной прямой, при этом конечная точка является центром окружности, а наклонная прямая — радиусом вращения.

Принцип поворота для получения действительной длины: на диаграмме ниже показан принцип поворота для получения действительной длины. ab — линия общего положения, наклонная к любой плоскости проекции. Проекция ab a'b' на плоскость V и проекция ab на плоскость H короче действительной длины. Предполагая, что ось AO перпендикулярна плоскости H на одном конце AB, при повороте AB вокруг оси AO в положение AB1, параллельное плоскости V, его проекция a'b1′ на плоскость V (пунктирная линия на диаграмме обозначает действительную длину) будет отражать его действительную длину.

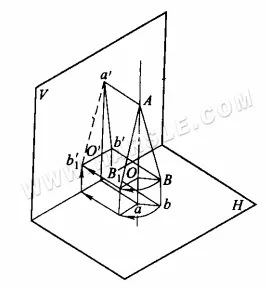
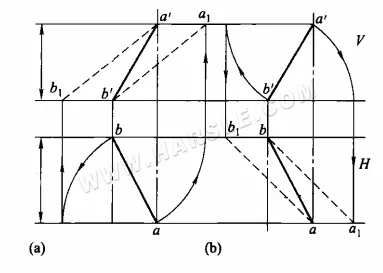
Метод вращения для действительных длин: На диаграмме ниже показан конкретный метод использования метода вращения для действительных длин. На диаграмме ниже (a) горизонтальная проекция ab поворачивается так, чтобы она стала параллельной ортогональной проекции, в результате чего образуются точки a1 и b1, соединяющие точки a1b' или a'b1, что является действительной длиной отрезка AB; на диаграмме ниже (b) ортогональная проекция a'b' поворачивается так, чтобы она стала параллельной горизонтальной проекции, в результате чего образуются точки a1 и b1, соединяющие точки a1b' или a'b1, что является действительной длиной отрезка AB.

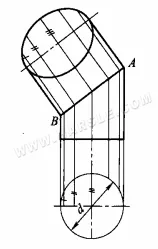
Пример: На рисунке ниже показана диаграмма действительной длины наклонной призмы, полученная методом вращения. Как видно из проекции, основание наклонной призмы параллельно горизонтальной плоскости, а её горизонтальная проекция отражает её объёмную форму и действительную длину. Остальные четыре грани (стороны) представляют собой два набора треугольников, проекции которых не отражают их действительную форму. Чтобы получить действительную форму двух наборов треугольников, необходимо найти действительную длину их призм. Поскольку фигура симметрична спереди назад, для построения диаграммы требуются только действительные длины двух боковых призм.

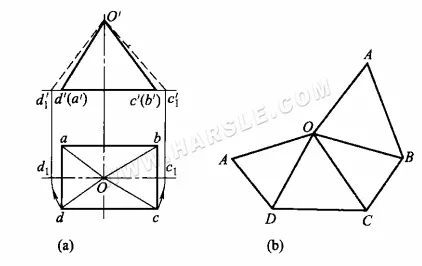
Конкретные шаги по созданию развёрнутой диаграммы:

1. Используя метод вращения, найдите действительные длины боковых рёбер Oc и Od. Как показано на рисунке ниже, примем точку O за центр окружности, а Oc и Od — за радиус вращения. Пересечём горизонтальную прямую в точке c1, d1. Проекция c1, d1 от точки c1, d1 вверх по вертикальной прямой. Продолжение ортографической проекции c'd', пересекающей точку c1'd1′ и соединяющей точки O'c1′ и O'd1′, будет действительной длиной боковой стороны призмы Oc и Od.

2. Проведите отрезок AD длиной, равной ad, в соответствующем месте на диаграмме, затем начертите △AOD, где A и D — центры окружностей, а Od' — радиус дуги, пересекающий точку O. Затем проведите дугу, где O — центр окружности, а Oc1′ — радиус, пересекающую дугу, построенную с центром D и радиусом dc, в точке C. Соедините OC и DC, чтобы получить △DOC. Начертите оставшиеся две стороны △COB и △BOA таким же образом, чтобы получить треугольный конус с развернутыми сторонами.

Рисунок ниже представляет собой усеченный конус, действительную длину конуса и расширение, сначала следует нарисовать вершину конуса, чтобы получился полный конус, а затем создать ряд конических поверхностей и использовать метод вращения, чтобы найти, что эти линии являются усеченной частью действительной длины линии (также доступно оставить часть действительной длины линии), вы можете сделать расширение фигуры.

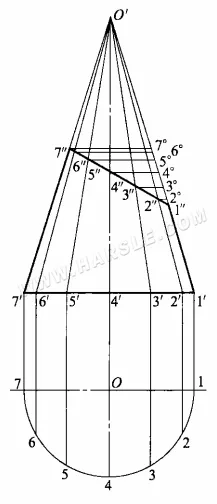
Чтобы найти действительную длину усеченной части линии, необходимо выполнить следующие шаги построения диаграммы.

1. Продлите линии фигуры на 1'1″ и 7'7″ до пересечения, получив в результате вершину конуса O'.

2. Постройте окружность основания конуса и разделите окружность основания на несколько равных частей (здесь 1/2 окружности основания делится на 6 равных частей), чтобы получить равные части 1, 2, …, 7, из каждой равной точки до главного вида вертикального отвода и ортогональной проекции окружности основания, пересекающейся в точках 1′, 2′, …, 7′, а затем из каждой точки и вершины конуса O' для линии, чтобы получить конус, линии конической поверхности.

3. Среди линий конуса только линии контура 1″1′ и 7″7′ параллельны ортогональной проекции и отражают её длину, в то время как остальные линии не отражают её действительную длину. Метод заключается в том, чтобы провести параллельную линию длиной 7'1′ из отрезков 7″, 6″…, 2″ и пересечь линию контура O'1′ под углами 7°, 6°…, 2°, O'6°, O'5°…, O'2° для O'6″, O'5″…, O' 2″ соответственно. 2″ действительной длины.

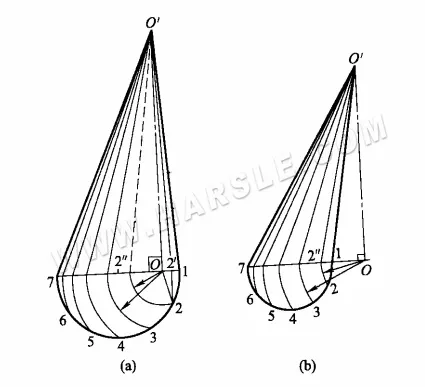
На диаграмме выше показана реальная длина косого конуса, полученная в результате вращения. Процесс следующий.

1. Сначала разделите 1/2 окружности основания на несколько равных частей (на схеме — на 6 равных частей).

2. с вертикальным основанием О в качестве центра окружности, O1, O2, …, O6 для радиуса дуги и пересечения линий 1 ~ 7 в 2 дюймах и так далее в каждой точке.

3. Проведите линию от точек 2″ и т.д. до точки O', где O'2′ и т.д. — истинная длина линии, проходящей через точки равноденствия. Другими словами, O'2′ — это ортогональная проекция линии O2, а O'2″ — истинная длина линии O2.

На диаграмме ниже показаны действительные длины призм квадратного соединения при использовании метода вращения и их расширения.

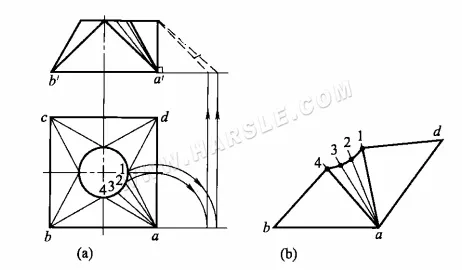
Шаги для рисования реальных длин призм следующие:

1. начертите основной вид и вид сверху, уравняйте отверстие круга вида сверху и соедините соответствующие простые линии.

2. Поверните простые линии a1, (a4), a2, (a3) и проведите вертикальные линии вверх, чтобы получить их действительные длины a-1, (a-4) и a-2, (a-3) на правой стороне основного вида.

3. Используя реальные длины простых линий, длины кромок квадратного горлышка и эквивалентные длины дуг круглого горлышка, поочередно начертите четверти горлышка.

В месте перехода квадратной трубы в круглую трубу необходимо наличие соединения квадрат-круглая труба. Квадратное отверстие может быть квадратным или прямоугольным, круглое отверстие может располагаться по центру, сбоку или в углу, поэтому форма таких соединений может быть различной, но метод определения фактической длины квадратного и круглого соединений в принципе одинаков.

Метод прямоугольного треугольника

Метод прямоугольного треугольника — это широко используемый метод нахождения действительной длины.

Принцип метода прямоугольного треугольника и метод черчения: следующая диаграмма (a) является принципиальной диаграммой метода прямоугольного треугольника для действительной длины. Отрезок AB не параллелен плоскости проекции, а его проекции ab и a'b' не отражают действительную длину. В плоскости ABba проведена прямая, параллельная ab, через точку A и пересекающая Bb в точке B1, давая прямоугольный треугольник ABB1. В этом треугольнике действительная длина гипотенузы AB прямоугольного треугольника может быть найдена, зная длины двух прямоугольных катетов AB1 и BB1. А длины AB1 и BB1 находятся на диаграмме проекции как AB1 = ab, BB1 = b'b1′ или BB1 = b'bx – a'ax. Знание таких двух прямоугольных катетов однозначно рисует искомый прямоугольный треугольник.

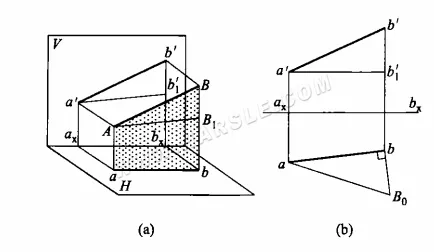
На рисунке (b) выше показано использование метода прямоугольного треугольника для определения действительной длины. Проекция линии AB обозначается как ab и a'b'. Чтобы найти действительную длину AB, сначала проведите горизонтальную линию через точку a', пересечь линию bb' в точке b1′, где bb1′ — это длина стороны прямого угла. Затем проведите вид сверху на ab для другого ребра прямого угла через точку b, указанную вертикальной линией, и пересеките линию bB0 = b'b1′, соединив её с aB0, то есть действительной длиной отрезка.

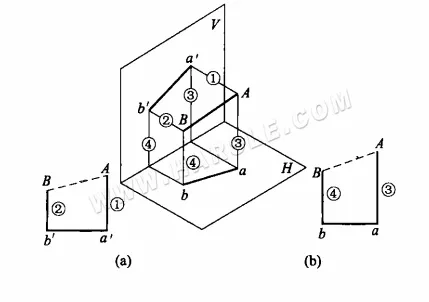
Пример: На диаграмме ниже показаны маленькое и большое квадратное соединение. Попробуйте найти действительную длину его основной линии AC и вспомогательной линии BC.

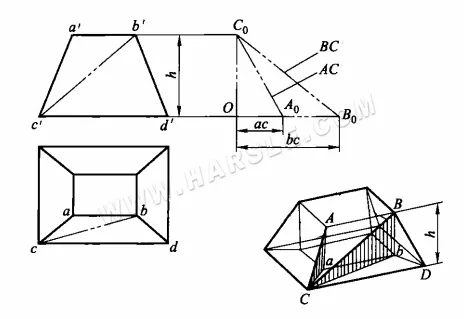
Из рисунка видно, что действительная длина AC может быть найдена в прямоугольном треугольнике, где aC и Aa – две прямоугольные стороны, а действительная длина BC – в прямоугольном треугольнике BbC. В обоих треугольниках Aa = Bb = h, что равно высоте сочленения. Две другие прямоугольные стороны aC и bC равны проекциям ac и bc сторон AC и BC на виде сверху соответственно. Таким образом, действительные длины сторон AC и BC можно найти следующим образом.

1. постройте прямой угол B0OC0.

2. точки пересечения OA0 и OB0 на горизонтальной стороне этого прямого угла, равные соответственно ac и bc на виде сверху, и точка пересечения OC0 на вертикальной стороне, равная высоте h на виде сверху.

3. соедините C0A0 и C0B0, тогда гипотенузы C0A0 и C0B0 будут действительными длинами искомых AC и BC.

Метод прямоугольной трапеции

Метод прямоугольных трапеций также является распространенным методом нахождения действительных длин.

Принцип метода прямых трапеций для действительной длины и метод построения: на следующей диаграмме показан принцип использования метода прямых трапеций для действительной длины. Общее расположение линии AB на поверхностях V и H не может отражать действительную длину, но две конечные точки линии AB и расстояние между поверхностью V могут быть получены на поверхности H, то есть Aa и Bb, то же самое, две точки A, B и расстояние между поверхностью H также могут быть получены на поверхности V, то есть Aa 'и Bb'. Основываясь на этом принципе, действительную длину линии AB можно найти с помощью метода прямых трапеций. Существует два конкретных метода построения графика действительной длины.

1. используя ортографическую проекцию действительной длины линии AB: ортографическая проекция AB a'b' как нижнего края прямоугольной трапеции, из двух точек a', b' соответственно вверх по вертикальной линии, отсекаем длину Aa', Bb', соединенную с AB, то есть для требуемого.

2. использование горизонтальной проекции действительной длины отрезка прямой AB: горизонтальная проекция AB как нижнего края прямоугольной трапеции, из точек a и b соответственно вверх по вертикальной линии, отсекаемая длина Aa, Bb, соединяется AB, что и является искомым.

Пример: на следующем рисунке показан подковообразный деформационный сустав, его верхняя и нижняя части представляют собой окружности, но обе окружности не параллельны и не равны по диаметру, попробуйте построить метод прямоугольной трапеции из его длины линии и диаграммы расширения.

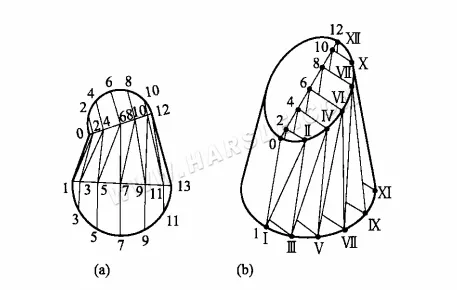
Из рисунка (a) выше видно, что, поскольку его поверхность не является конической, для построения его диаграммы расширения достаточно использовать линию, соединяющую поверхность и выходящую из неё, в несколько треугольников, и поочередно находить истинную форму этих треугольников. Конкретные этапы построения графика следующие.

1. Сделайте 12 равных частей верхнего и нижнего рта и разделите поверхность на 24 треугольника, как показано на рисунке.

2. Найдите действительные длины прямых Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII, а затем постройте действительную форму ряда треугольников.

В таких случаях, если для определения действительной длины используется метод вращения или метод прямоугольного треугольника, необходимо выполнить проекцию отрезка на вид сверху. Поскольку верхняя поверхность подковообразного деформационного соединения и горизонтальная плоскость проекции наклонены, то верхняя поверхность на виде сверху отражается в виде эллипса. Очевидно, что эти два метода расширения карты представляют собой более сложную задачу. В настоящее время целесообразно использовать метод прямоугольных трапеций.

Например, на рисунке (b) в сложенной поверхности Ⅰ-1-Ⅱ-2-Ⅲ-3…XII-12, растянутой в фигуру, показанную ниже, затем фигуру над линией сгиба Ⅰ-Ⅱ-Ⅲ…XII, то есть действительную длину Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII и так далее. Этот метод нахождения действительной длины называется методом прямоугольных трапеций.

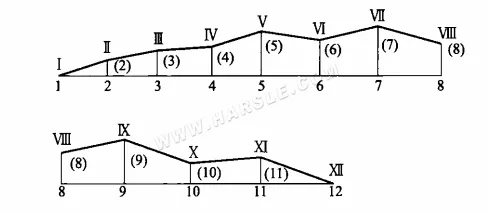
Как видно из метода построения диаграммы, метод прямоугольных трапеций также основан на проекции наклонной линии в качестве основания, при этом расстояние между двумя концами наклонной линии и той же плоскостью проекции, что и расстояние между двумя прямыми сторонами, после построения прямоугольной трапеции, равно гипотенузе прямоугольной трапеции, то есть действительной длине искомой линии. Прямоугольный треугольник можно рассматривать как частный случай метода прямоугольных трапеций, где длина прямого катета равна нулю.

Вышеуказанным способом получают две боковые линии каждого треугольника на поверхности подковообразного деформационного шва, другая сторона которого представляет собой длину верхнего и нижнего круговых отверстий, равную развёрнутой дуге. Таким образом, методом треугольников с тремя известными сторонами можно построить ряд треугольников, которые располагаются таким образом, чтобы получить следующую диаграмму подковообразного деформационного шва.

Метод изменения лица

Помимо вышеперечисленных методов нахождения действительной длины линии, существует также распространенный метод изменения поверхности.

Принцип метода изменения поверхности для получения действительной длины и метод построения: принцип метода изменения поверхности заключается в том, чтобы сохранить отрезок пространства неизменным, а затем создать новую проекционную поверхность, параллельную заданному отрезку и перпендикулярную исходной. Проекция отрезка на новую проекционную поверхность будет отражать его истинную длину. На рисунке выше схематично изображена действительная длина отрезка.

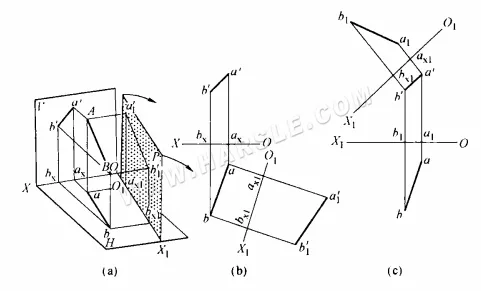
Как видно из рисунка (а), отрезок AB не параллелен ни плоскостям проекций H, ни плоскостям проекций V, и его проекция не отражает действительную длину. Новая проекция a1'b1′ отражает действительную длину отрезка AB. Дальнейший анализ пространства, показанного на рисунке (а), выявляет следующие проекционные соотношения для метода изменения поверхности.

1. Поскольку новая проекционная поверхность P параллельна AB и перпендикулярна плоскости H, то линия пересечения между новой проекционной поверхностью P и плоскостью H, O1X1 (называемая новой проекционной осью), обязательно параллельна проекции ab на плоскость H прямой AB, O1X1 // ab, что отражается в проекции на плоскость H.

2. Поскольку поверхности P и V одновременно перпендикулярны поверхности H, расстояние от проекции a1'b1′ поверхности P до O1X1 и расстояние от проекции a'b' поверхности V до OX должны одновременно отражать перпендикулярные расстояния от двух конечных точек A и B пространственной линии до поверхности H, и они равны друг другу, a1ax1 = a'ax = Aa и b1'bx1 = Bb. Для простоты обозначения вновь созданная проекция, параллельная AB Проекция a1'b1′, которая отражает действительную длину, называется новой проекцией, проекция a'b', которая изначально не отражала действительную длину, называется старой или заменяющей проекцией, а проекция плоскости H, которая одновременно перпендикулярна им, называется инвариантной проекцией. Таким образом, это проекционное соотношение для метода заменяющей поверхности можно выразить как расстояние от новой проекции до новой оси, равное расстоянию от старой проекции до старой оси.

3. Поскольку поверхности P и V перпендикулярны поверхности H, соединение проекций P и H в любой точке на прямой должно быть перпендикулярно новой оси проекции O1X1, а прямая между инвариантной проекцией и старой и новой проекциями перпендикулярна старой и новой осям проекции соответственно после разворачивания.

В соответствии с приведенным выше проекционным соотношением метода перестановки шаги построения графика должны быть следующими:

1. как показано в (b) выше, сделайте новую ось проекции O1X1 параллельной ab.

2. Проведем перпендикулярную прямую через точки a и b к оси O1X1 и пересечем O1X1 в точках ax1 и bx1.

3. Переместите проекции a' и b' плоскости V на ось OX в новую плоскость проекции, измерьте ax1a1'=axa' и bx1b1'=bxb' на вертикальных линиях.

4. Соединяем точки a1′ и b1′, получаем новую проекцию a1'b1′ линии AB, которая отражает действительную длину AB.

Пример: На диаграмме ниже показано использование метода вспомогательной проекционной плоскости для нахождения действительной формы цилиндрического сечения.

Этапы рисунка следующие.

1. сделайте основной и верхний вид, разделив верхний вид на 1/2 длины окружности на 6 равных частей.

2. Проведите вертикальную линию вверх через равноудалённую точку, чтобы указать положение основной линии на главном виде.

3. Проведем перпендикуляры вниз из равноудаленных точек до пересечения с нижней центральной линией, ширина между линиями сечения

4. проведение перпендикулярных линий через точку пересечения линий на косом отверстии сечения до длинной оси, параллельной косому отверстию сечения, а затем проведение расстояния между равноудаленными точками на виде сверху и центральной линией нижнего круга, в свою очередь, до точек на вторичном виде в соответствии с правилом «равной ширины».

5. Соедините точки так, чтобы получился сплошной эллипс сечения.

На рисунке ниже показано применение метода вспомогательной плоскости проекции для нахождения действительной формы сечения ортокуна. Рисунки ①, ②, … (7) указывают порядок построения и соединения линий.

Как правило, для построения реальной формы конического сечения не требуется проводить линии на поверхности конуса, но лучше использовать метод уточной окружности, как показано на рисунке выше. Для наглядности линии в данном примере будут представлены по отдельности три этапа построения диаграммы, саму диаграмму разделять не нужно. Этапы построения следующие.

1. Окружности утка: проекционная линия сечения делится на 6 равных частей; горизонтальная линия, проведенная через указанные равные точки, пересекается с линией контура; вертикальная линия проводится вниз из каждой точки пересечения на линии контура и пересекается в нижней части конуса; окружности утка поочередно проводятся с центром окружности О, см. рисунок (а) выше.

2. Вид сверху на поперечное сечение: проведя вертикальную линию вниз через каждую точку пересечения линий поперечного сечения на главном виде, пересекающуюся с соответствующей окружностью широты, получаем ряд точек пересечения; соединив точки пересечения, можно получить проекцию поперечного сечения сверху, см. рисунок (b) выше.

3. Чтобы найти действительную форму сечения: постройте эллипс, параллельный длинной оси сечения 1″7″; проведите перпендикулярные линии из каждой равной точки сечения 1~7 к длинной оси 1″7″; в соответствии с принципом равной ширины, проведите ряд значений ширины a, b, c, d и e сечения на виде сверху до вспомогательной проекции, получив в результате точки 2″, 3″, 4″, 5″ и 6″; соедините точки, то есть действительную форму конического сечения, см. диаграмму (b) выше. Рисунок (c) выше.

На диаграмме ниже показано использование метода вспомогательной проекционной поверхности для нахождения действительной формы косого конического сечения.

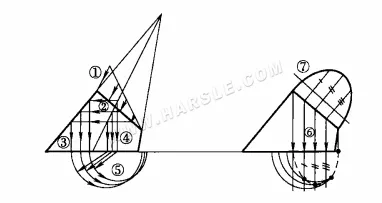
Использование вспомогательного вида для построения действительной формы косого конического сечения аналогично использованию действительной формы ортогонального конического сечения. Однако косой конус имеет особенность: его вершина наклонена в одну сторону, а его ось также наклонена, так что центры ряда уточных окружностей не лежат в одной точке на одной оси. Поэтому вместо построения концентрических окружностей строится конус с одним центром для каждой уточной окружности. Этой особенностью можно овладеть, выполнив три описанных выше шага построения вспомогательного вида сечения тела.

Конкретные этапы рисования следующие.

1. Для уточной окружности: линия сечения 4 равных частей; для равных точек горизонтальной линии, пересекающей линию контура; от линии контура по точкам вниз до вертикальной линии, пересекающей нижнюю окружность; для уточной окружности равные точки горизонтальной линии и оси пересечения точек центра, центр окружности до нижней окружности; соответственно центр уточной окружности и соответствующий радиус для уточной окружности.

2. Вид сечения сверху: через главный вид линий сечения каждого эквивокента, вертикальные линии, направленные вниз, и соответствующую точку пересечения окружности широты, в результате чего образуется ряд точек пересечения; вместе с точками пересечения можно получить вид сечения сверху.

3. Чтобы построить действительную форму сечения: в соответствии с шириной формы сечения, найденной на виде сверху, сделайте вспомогательный вид 1/2, чтобы нарисовать 1/2 действительной формы косого конического сечения.

Сравнение методов реальной длины

На основе вышеприведенного анализа можно провести простое сравнение четырех методов нахождения действительной длины действительной линии.

Метод вращения позволяет найти действительную длину путем изменения положения фигуры в пространстве, не меняя положения плоскости проекции.

Метод перестановки позволяет найти действительную длину путем изменения положения плоскости проекции, не меняя положения фигуры.

Метод прямоугольного треугольника и метод прямоугольной трапеции (метод прямоугольного треугольника можно рассматривать как частный случай метода прямоугольной трапеции) позволяют получить прямую действительной длины, не изменяя ни положения пространственной фигуры, ни положения плоскости проекции.