Le calcul de la disposition correcte du modèle plat est essentiel pour obtenir une pièce finie de bonne qualité de votre part. presse plieusePourtant, de nombreux programmeurs CAO et CNC ignorent totalement comment calculer les valeurs requises. Autrefois, les véritables experts créaient des aide-mémoire et les affichaient au mur. Ils apprenaient seulement aux nouveaux apprentis à appliquer les résultats indiqués, et non à calculer les valeurs. Aujourd'hui, ces experts ont pris leur retraite et il est temps pour une nouvelle génération d'apprendre à calculer correctement la mise à plat. Vous pouvez également utiliser notre calculateur de tolérance de pliage ou calculateur de déduction de courbure pour obtenir les résultats facilement.

Calculer la longueur du modèle à plat à partir de la pièce 3D n'est pas si difficile. Cependant, plusieurs formules prétendent le faire. calculer le Tolérance de pliage (voir Définitions de pliage). Il s'agit généralement de la même formule, simplifiée par l'ajout de l'angle ou d'un facteur K. Bien sûr, il est nécessaire de connaître le facteur K pour calculer la tolérance de pliage.

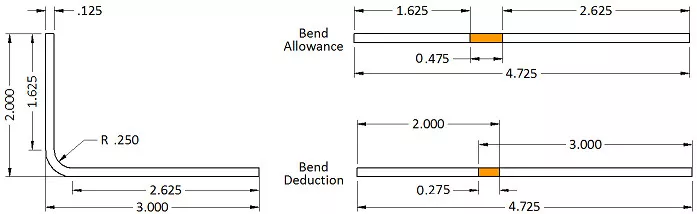
Prenons l'exemple d'un support en L simple. Il comporte deux branches, l'une de 5 cm et l'autre de 7,6 cm, avec une épaisseur de matériau de 3,1 cm et un rayon de courbure intérieur de 6,3 cm. L'angle de courbure est de 90 degrés. Pour déterminer la longueur à plat, on ne mesure ni à partir de la surface intérieure ni de la surface extérieure, mais à partir de l'axe neutre. C'est là qu'intervient le facteur K. Ce facteur représente la position de l'axe neutre en pourcentage de l'épaisseur du matériau. Pour ce calcul, nous utiliserons un facteur K de 0,42 pour déterminer la tolérance de pliage et le plan de travail corrects.

La formule (voir Formules de pliage) est : 

Tolérance de pliage = Angle * (π / 180) * (Rayon + facteur K * Épaisseur). 

En insérant nos chiffres, nous avons : Tolérance de courbure = 90 * (π / 180) * (0,250 + 0,42 * 0,125) = 0,475″

La longueur du modèle à plat est donc de 1,625" + 2,625" + 0,475", soit 4,725". En additionnant la longueur à plat de toutes les brides et en ajoutant une marge de pliage pour chaque zone de pliage, vous obtenez la longueur à plat correcte de la pièce.

Examinons maintenant le dessin de plus près. En conception de tôlerie, les cotes sont généralement données à l'intersection des ailes, appelée ligne de moulage. De ce fait, il faut soustraire du total deux fois l'épaisseur du matériau et le rayon de pliage pour tenir compte de chaque zone de pliage. Cette valeur est appelée « décalage ». Dans ce cas, l'utilisation de la compensation de pliage est souvent plus simple. Cette fonction permet d'utiliser les cotes de la ligne de moulage pour chaque aile, puis d'ajuster le total en ajoutant une valeur de compensation par pliage. Ici, la compensation est de -0,275 ; 5 pouces deviennent donc 4,725 pouces après soustraction.

Définitions :

Tolérance de pliage = Angle * (π / 180) * (Rayon + Facteur K * Épaisseur) 

Compensation de courbure = Tolérance de courbure – (2 * Retrait)

Retrait intérieur = tan (angle / 2) * rayon extérieur 

Recul = tan (Angle / 2) * (Rayon + Épaisseur)

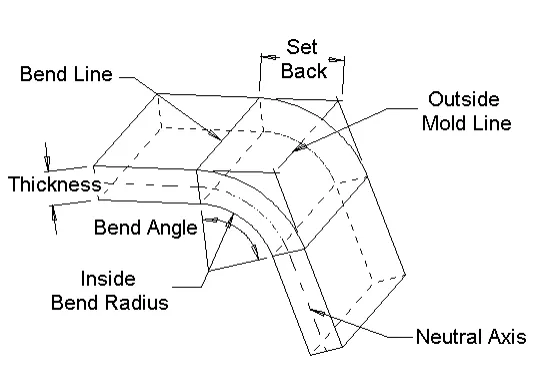
tolérance de pliage – La longueur de l’arc à travers la zone de courbure au niveau de l’axe neutre.

Angle de courbure – L’angle inclus de l’arc formé par l’opération de pliage.

Compensation de courbure – L'étirement ou la compression du matériau lors de l'opération de pliage. L'étirement ou la compression est supposé se produire dans la zone de pliage.

Lignes de courbure – Les lignes droites sur les surfaces intérieures et extérieures du matériau où la limite de la bride rencontre la zone de pliage.

Rayon de courbure intérieur – Le rayon de l’arc sur la surface intérieure de la zone de courbure.

facteur K – Définit l'emplacement de l'axe neutre. Il est mesuré comme la distance entre l'intérieur du matériau et l'axe neutre, divisée par l'épaisseur du matériau.

Lignes de moulage – Pour les pliages de moins de 180 degrés, les lignes de moulage sont les lignes droites d'intersection des surfaces de la bride délimitant la zone de pliage. Ceci se produit sur les surfaces intérieures et extérieures du pliage.

Axe neutre – En regardant la section transversale du coude, l’axe neutre est l’emplacement théorique où le matériau n’est ni comprimé ni étiré.

Recul – Pour les coudes de moins de 180 degrés, le retrait est la distance entre les lignes de pliage et la ligne de moulage.

Comment calculer le facteur « K » :

À ma connaissance, il n'existe pas de formule pour calculer le facteur k. Oh, je suis sûr qu'un ingénieur mathématicien en possède une quelque part. Mais elle est probablement trop complexe pour que la plupart d'entre nous la comprennent ou puissent l'utiliser.

Le facteur k est le pourcentage de l'épaisseur du matériau où il n'y a ni étirement ni compression dans la zone de pliage. Ainsi, l'axe neutre !

Plus le matériau est dur, moins la compression est importante à l'intérieur du pli. Par conséquent, l'étirement est plus important à l'extérieur, et l'axe neutre se déplace vers l'intérieur du pli. Les matériaux plus souples permettent une compression plus importante à l'intérieur, et l'axe neutre reste plus proche du centre de l'épaisseur du matériau.

Le rayon de courbure a un effet similaire. Plus le rayon de courbure est petit, plus le besoin de compression est important et l'axe neutre se déplace vers l'intérieur du pli. À un rayon plus grand, l'axe neutre reste proche du centre de l'épaisseur du matériau.

Facteurs K génériques	Aluminium		Acier
Rayon	Matériaux souples	Matériaux moyens	Matériaux durs
Flexion de l'air
0 à épaisseur	0.33	0.38	0.40
Épaisseur jusqu'à 3×épaisseur	0.40	0.43	0.45
Plus de 3×épaisseur	0.50	0.50	0.50
Toucher le fond
0 à épaisseur	0.42	0.44	0.46
Épaisseur jusqu'à 3×épaisseur	0.46	0.47	0.48
Plus de 3×épaisseur	0.50	0.50	0.50
frappe de monnaie
0 à épaisseur	0.38	0.41	0.44
Épaisseur jusqu'à 3×épaisseur	0.44	0.46	0.47
Plus de 3×épaisseur	0.50	0.50	0.50

La formule suivante peut être utilisée à la place du tableau comme une bonne approximation du facteur K pour la flexion de l'air :

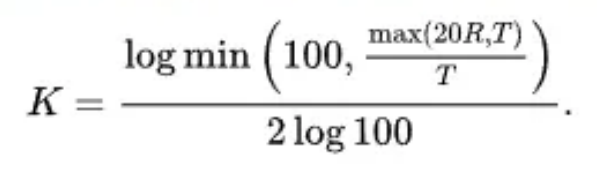
Diagramme et formules de calcul de la tolérance de pliage

Afin de vous aider à maîtriser plus facilement et plus rapidement la formule de calcul de la longueur de pliage dépliée, nous avons répertorié quatre tableaux de coefficients courants, illustré seize formules de calcul de la longueur de pliage dépliée et utilisé quelques exemples pour une meilleure compréhension. Nous espérons que les informations suivantes vous seront utiles. Pour toute question, n'hésitez pas à nous contacter.

Largeur de la rainure en V/épaisseur de la plaque	0.6	0.8	1.0	1.2	1.5	2.0	2.5	3.0	3.5	4.0	4.5	5.0	Taille la plus courte
V4	0.9	1.4											2.8
V6		1.5	1.7	2.0									4.5
V7			1.8	2.1	2.4								5.0
V8			1.9	2.2	2.5								5.5
V10			2.1	2.3	2.7								7.0
V12			2.2	2.5	2.8	3.4							8.5
V14						3.5	3.8			6.4	6.8		10.0
V16					3.1	3.8	4.5	5.0					11.0
V18					3.3	4.0							13.0
V20						4.0	4.9	5.1		6.6	7.2	7.8	14.0
V25						4.4	5.0	5.5		6.8	7.8	8.3	16.5
V32						5.0	5.5	6.1		8.7

Note: Lorsque la taille graphique de la pièce est marquée avec une tolérance négative, la valeur du facteur de flexion peut être augmentée, comme indiqué dans le tableau, la partie rouge peut être augmentée à : 2,8 ; 2,82 ; 3,4 ; 3,43 ou 3,44 : 4,5 ; 4,6 ; 5,5 : 5,6

Épaisseur mm\angle	Rainure du moule largeur		90°	Coin intérieur	Coin extérieur		180°
1.5	V10		3.0	3.2	4.1		0.8
2.0	V12		3.8	3.7	4.6		1.0
2.5	V16		4.5	4.8	6.1		1.3

Épaisseur  mm\angle	30°		45°		60°			120°			135°			145°
1.0	0.35		0.7		1.1			1.0			0.6			0.4
1.2	0.4		0.8		1.2			1.0			0.6			0.4
1.5	0.5		1.0		1.6			1.4			0.9			0.6
2.0	0.6		1.2		2.0			1.7			1.1			0.7
2.5	0.8		1.6		2.6			2.2			1.4			0.85
3.0	1.0		2.2		3.4			2.8			2.0			1.2
4.0								3.7			2.4			1.4

Épaisseur mm		0.5	1.0	1.2		1.5	2.0		2.5	3.0		4.0	5.0		6.0
Trou de traitement mm		1. Pas de trous 2.Peut ouvrir le trou φ2		φ2		φ2,5	φ3.0		φ3,5	φ4.0		φ5,5	φ6.0		φ7.0

Note: Si des besoins particuliers sont autorisés, une ouverture de plus grande taille peut être utilisée.

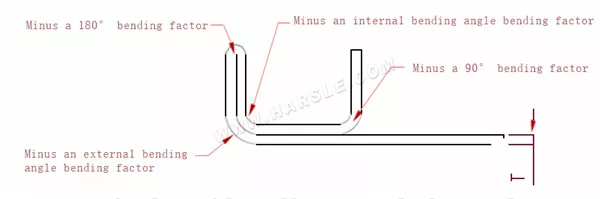
Schéma et formule de calcul pour un coude

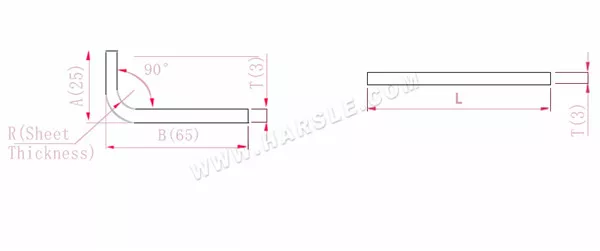
A, B — longueur de pliage de la pièce

P' — coefficient de flexion des bords (facteur de flexion : un facteur moins une courbure)

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

La longueur développée L=A+B-P', qui est L=25+65-5,5=84,5

Selon le tableau 1, l'épaisseur de la plaque est de 3, la matrice inférieure est V25 et le coefficient de flexion est de 5,5

Remarque : selon le tableau 1, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Schéma et formule de calcul du coude à deux coudes

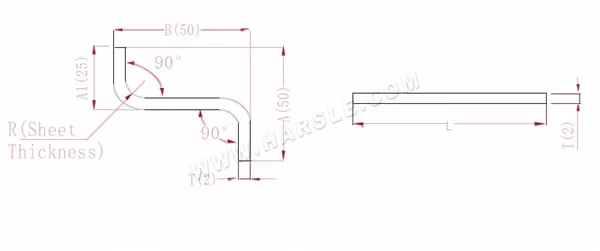
A(A1), B— longueur de pliage de la pièce

P' — coefficient de flexion des bords (facteur de flexion : un facteur moins une courbure)

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

La longueur développée L=A+T+B-2*P', qui est L=50+2+50-2*3,4=95,2

Selon le tableau 1, l'épaisseur de la plaque est de 2, la matrice inférieure est V12 et le coefficient de flexion est de 3,4

Remarque : selon le tableau 1, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Schéma et formule de calcul du coude à trois coudes

A(A1), B(B1)-longueur de pliage de la pièce

P' — coefficient de flexion des bords (facteur de flexion : un facteur moins une courbure)

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

La longueur développée L=A+T+B+T-3*P', soit L=50+2+90+2-3*3,4=133,8

Selon le tableau 1, l'épaisseur de la plaque est de 2, la matrice inférieure est V12 et le coefficient de flexion est de 3,4

Remarque : selon le tableau 1, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Schéma et formule de calcul du quadri-coude 

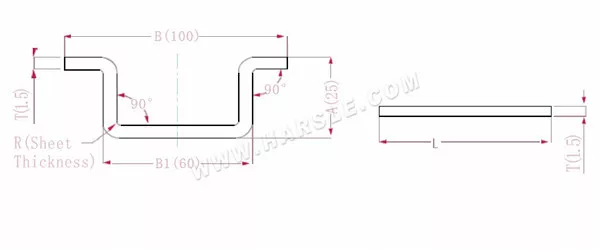
A, B (B1) - longueur de pliage de la pièce

P' — coefficient de flexion des bords (facteur de flexion : un facteur moins une courbure)

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

La longueur développée L=A+A+B+T+T-4*P', soit l = 25+25+100+1,5+1,5-4 * 2,8 = 141,8

Selon le tableau 1, l'épaisseur de la plaque est de 1,5, la matrice inférieure est V12 et le coefficient de flexion est de 2,8

Remarque : selon le tableau 1, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Schéma et formule de calcul du six-bend 

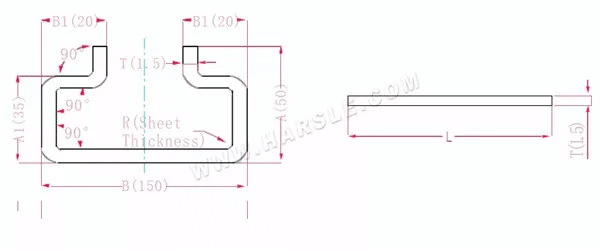
A(A1), B(B1)-longueur de pliage de la pièce

P' — coefficient de flexion des bords (facteur de flexion : un facteur moins une courbure)

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

La longueur d'extension L=A+T+A+T+B+B1+B1-6*P'

qui est l = 50+1,5+50+1,5+150+20+20-6 * 2,8 = 276,2

Selon le tableau 1, l'épaisseur de la plaque est de 1,5, la matrice inférieure est V12 et le coefficient de flexion est de 2,8

Remarque : selon le tableau 1, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Schéma et formule de calcul de pliage à 180 degrés

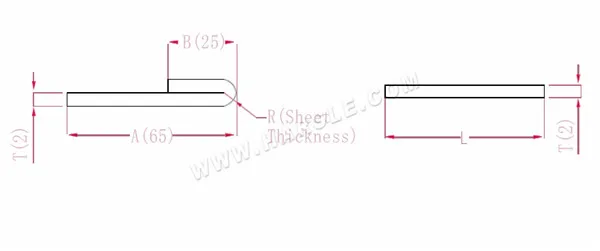
A, B — longueur de pliage de la pièce

P' — coefficient de flexion du congé d'aplatissement

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

La longueur développée L=A+B-P', qui est L=25+65-1=89

Selon le tableau 2, l'épaisseur de la plaque est de 2, la matrice inférieure est V12 et le facteur de flexion est la moitié de l'épaisseur de la plaque.

Remarque : selon le tableau 2, la sélection de différentes matrices inférieures présente des coefficients de flexion différents et des épaisseurs de plaque différentes.

Schéma et formule de calcul de la flexion à double couche 

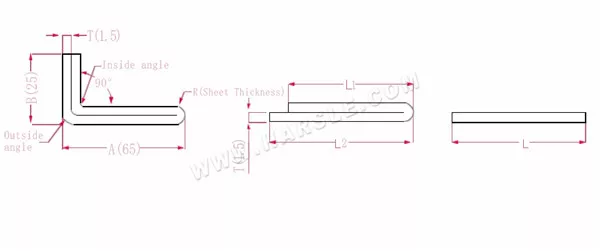
A, B — longueur de pliage de la pièce

P1 — coefficient de flexion du coin intérieur

P2 — coefficient de flexion de l'angle de flexion externe

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

La longueur étendue L1=(A-1,5) +(B-1,5)-P1, soit L1= (65-1,5) +(25-1,5)-3,2=83,8

L2=A+B-P2, soit L2=65+25-4,1=85,9

L=L1+L2-T/2, soit L=83,8+85,9-0,75=168,95

Selon le tableau 2, l'épaisseur de la plaque est de 1,5, la matrice inférieure est V12, le coefficient de flexion du coin intérieur est de 3,2, le coefficient de flexion du coin extérieur est de 4,1 et le coefficient de flexion à 180 est de 0,75.

Remarque : Selon le tableau 2, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Schéma et formule de calcul du pliage à double couche avec un bord

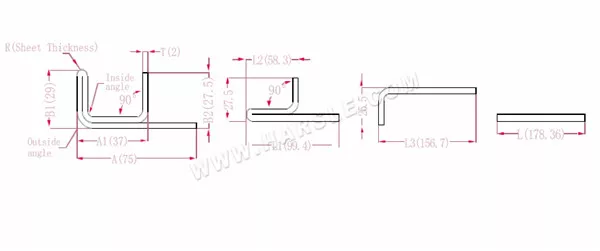
A, A1, A2, B1, B2, L, L1, L2, L3 — longueur de pliage de la pièce

P1 — coefficient de flexion du coin intérieur

P2 — coefficient de flexion de l'angle de flexion externe

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

La longueur étendue L1=(A1-T) +(B2-T)-P1 qui est L1= (35-2) +(34-2)-3,7=61,3

L2=(B1-T) +(A2-T)-P1, soit L2= (50-2) +(34-2)-3,7=76,3

L3=A+B1+B2-2*P2, soit L3=70+35+50-2*4,6+145,8

L=L1+L2+L3-2*P3, soit L=61,3+75,3+145,8-2*1=280,4

Selon le tableau 2, l'épaisseur de la plaque est de 2, la matrice inférieure est V12, le coefficient de flexion du coin intérieur est de 3,7, le coefficient de flexion du coin extérieur est de 4,6 et le coefficient de flexion à 90° est de 1.

Remarque : Selon le tableau 2, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Schéma et formule de calcul du pliage à double couche avec deux bords

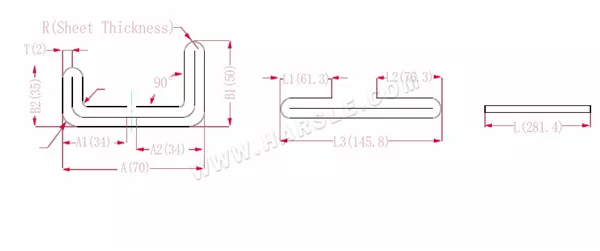
A, A1, A2, B1, B2, L, L1, L2, L3 — longueur de pliage de la pièce

P1 — coefficient de flexion du coin intérieur

P2 — coefficient de flexion de l'angle de flexion externe

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

La longueur étendue L1=(A1-T) +(B2-T)-P1 qui est L1= (35-2) +(34-2)-3,7=61,3

L2=(B1-T) +(A2-T)-P1, soit L2= (50-2) +(34-2)-3,7=76,3

L3=A+B1+B2-2*P2, soit L3=70+35+50-2*4,6+145,8

L=L1+L2+L3-2*P3, soit L=61,3+75,3+145,8-2*1=280,4

Selon le tableau 2, l'épaisseur de la plaque est de 2, la matrice inférieure est V12, le coefficient de flexion du coin intérieur est de 3,7, le coefficient de flexion du coin extérieur est de 4,6 et le coefficient de flexion à 90° est de 1.

Remarque : Selon le tableau 2, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Schéma et formule de calcul du pliage par gradins

A, B — longueur de pliage de la pièce

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

Longueur dépliée L=A+1

Remarque : Lorsque le pas est égal à l'épaisseur de deux plaques, ajoutez 0,5 pour chaque pas et 1 pour chaque pas.

Schéma et formule de calcul de l'angle spécial de pliage 1

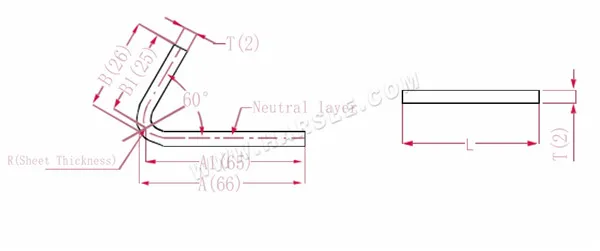
A(A1), B(B1)-longueur de pliage de la pièce

P' — coefficient de flexion des bords (facteur de flexion : un facteur moins une courbure)

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

La longueur d'extension L=(AT) +(BT)-P', qui est L= (66-1) +(26-1)-2=65+25-2=88

Selon le tableau 3, l'épaisseur de la plaque est de 2, la matrice inférieure est V12 et le coefficient de flexion à 60 est de 2

Remarque : selon le tableau 3, la couche neutre est sélectionnée comme longueur et largeur de courbure.

Schéma et formule de calcul de l'angle spécial de pliage 2

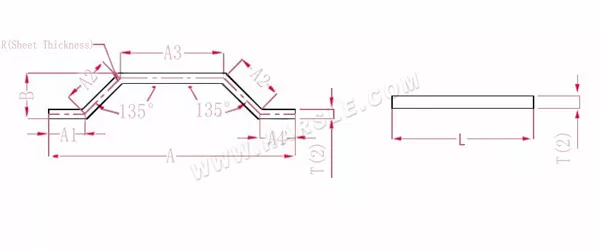
A (A1, A2, A3, A4), B — longueur de pliage de la pièce

P— facteur de flexion de 135 angles de flexion

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

La longueur d'extension L = A1+A2+A3+A2+A4-PP.

Remarque : la même flexion par palier de pression ne nécessite que la réduction de deux coefficients

Selon le tableau 3 : l'épaisseur de la plaque est de 2, la matrice inférieure est V12 et le coefficient de flexion à 135 est de 1,1.

Schéma et formule de calcul de l'angle spécial de pliage 3

A (A1, A2), B (B1, B2) - longueur de pliage de la pièce

P1—coefficient de flexion de 120°

P2—coefficient de flexion de 145°

P3 — coefficient de flexion à 90°

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

Remarque : si la taille du graphique est marquée sur la forme, la taille de la forme doit être convertie à la taille de la couche neutre lors du calcul de la longueur de dépliage ;

La longueur d'extension L=A11+B11+B21+A21-P1-P2-P3, soit l = 80+50+103+70-1,7-0,7-3,4 = 297,2

Selon le tableau 3 : l'épaisseur de la plaque est de 2, la matrice inférieure est V12, le coefficient de flexion à 120° est de 1,7, le coefficient de flexion à 145° est de 0,7 et le coefficient de flexion à 90° est de 3,4

Remarque : Selon le tableau 3, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Schéma et formule de calcul de la liaison commune 1

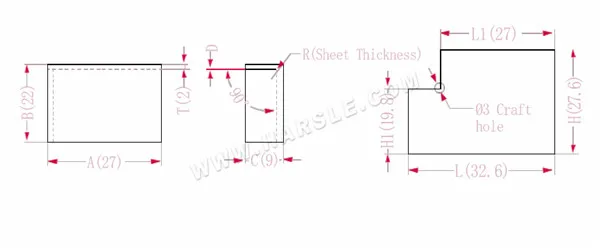
A, B, C — longueur, largeur et hauteur du bord de pliage de la pièce

P— coefficient de flexion

R — pliage et congé (généralement épaisseur de la plaque)

H(H1), l (L1) - la longueur dépliée de chaque côté

T — épaisseur du matériau

D — jeu du processus de pliage (généralement 0~0,5)

La longueur étendue L1=A, qui est L1=27

L=A+CP, soit L=27+9-3,4=32,6

H1=BTD, soit H1=22-2-0,2=19,8. Remarque : D est 0,2.

H=B+CP, soit H=22+9-3,4=27,6

Selon le tableau 1 : l'épaisseur de la plaque est de 2, la matrice inférieure est V12 et le coefficient de flexion est de 3,4

Remarque : selon le tableau 1, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Schéma et formule de calcul de la liaison commune 2

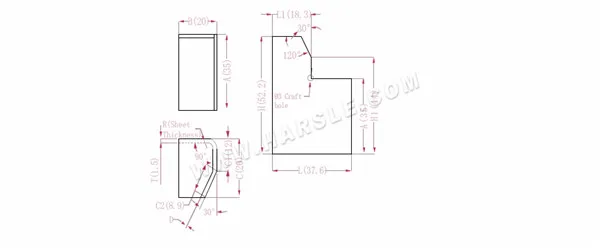
A, B, C — longueur, largeur et hauteur du bord de pliage de la pièce

H(H1), L (L1) - la longueur dépliée de chaque côté

P—coefficient de flexion à 90° P1—coefficient de flexion à 30°

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

D — jeu du processus de pliage (généralement 0~0,5)

La longueur étendue L1=BTD, qui est L1=20-1,5-0,2=18,3

L=B+C1+C2-P-P1, soit L=20+12+8,9-2,8-0,5=37,6

H1=C1+APD, soit H1=12+35-2,8-0,2=44. Remarque : D est 0,2.

H=A+CP, soit H=35+20-2,8=52,2

Selon le tableau 1 : l'épaisseur de la plaque est de 1,5, la matrice inférieure est V12, le coefficient de flexion est de 2,8 et le coefficient de flexion 30 est de 0,5

Remarque : selon le tableau 1, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Schéma et formule de calcul de la liaison commune 3

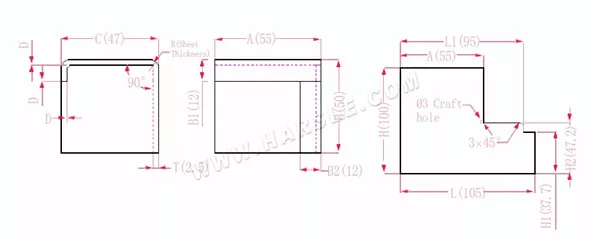
A, B, C — longueur, largeur et hauteur du bord de pliage de la pièce

H(H1), L (L1) - la longueur dépliée de chaque côté

P— coefficient de flexion

R — pliage et congé (généralement épaisseur de la plaque)

T — épaisseur du matériau

D — jeu du processus de pliage (généralement 0~0,5)

La longueur étendue H1=B-B1-D, soit H1=50-12-0,3=37,7. Remarque : D est 0,2.

H2=BTD qui est H2=50-2,5-0,3=47,2

H=B+C+B1-2*P, soit H=50+47+12-2*4,5=100

L1=A+CTDP, soit L1=55+47-2,5-0,3-4,5=94,7

L=A+C+B2-2*P, soit L=55+47+12-2*4,5=105

Selon le tableau 1 : l'épaisseur de la plaque est de 1,5, la matrice inférieure est V16 et le coefficient de flexion est de 4,5

Remarque : selon le tableau 1, les différents coefficients de flexion des matrices inférieures et des différentes épaisseurs de plaque sont différents.

Démo vidéo