Guia de cálculo de tolerância a dobras para freios de prensa

Calcular o layout correto do padrão plano é crucial para obter uma peça acabada de boa qualidade. Dobradeira. No entanto, muitos programadores de CAD e CNC não têm ideia de como calcular os valores necessários. Anos atrás, os verdadeiros especialistas criavam folhas de dicas e as pregavam na parede. Eles apenas ensinavam o novo aprendiz a aplicar os resultados mostrados na folha de dicas, não a calcular os números. Bem, agora esses especialistas se aposentaram e é hora de uma nova geração aprender a maneira correta de calcular o layout de padrão plano. Você também pode usar nosso calculadora de tolerância de curvatura ou calculadora de dedução de curvatura para obter os resultados facilmente.
Calcular o comprimento do padrão plano a partir da peça 3D não é tão difícil. Embora você possa encontrar várias fórmulas diferentes que afirmam calcular o Tolerância de Curvatura (consulte Definições de Curvatura). Geralmente, a fórmula é a mesma, simplificada apenas pelo preenchimento do ângulo ou de um fator K. Ah, e sim, você precisa saber o fator K para calcular a Tolerância de Curvatura.
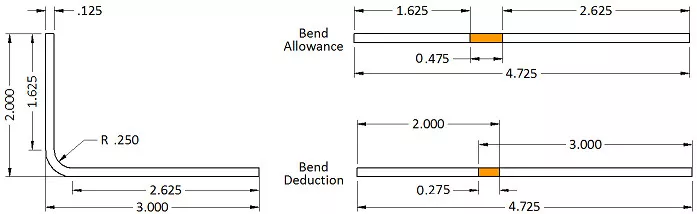
Tomemos como exemplo um suporte em L simples. Ele tem duas pernas, uma de 5 cm e a outra de 7,5 cm, com uma espessura de material de 0,31 cm e um raio de curvatura interno de 0,63 cm. O ângulo de curvatura é de 90 graus. Para encontrar o comprimento plano, não se mede a partir da superfície interna ou externa; em vez disso, considera-se o eixo neutro. É aqui que o fator K é usado. O fator K representa a posição do eixo neutro como uma porcentagem da espessura do material. Para este cálculo, usaremos um fator K de 0,42 para determinar a tolerância de curvatura e o padrão plano corretos.
A fórmula (ver Fórmulas de Dobra) é:
Tolerância de curvatura = Ângulo * (π / 180) * (Raio + Fator K * Espessura).
Substituindo nossos números, temos: Tolerância de curvatura = 90 * (π / 180) * (0,250 + 0,42 * 0,125) = 0,475″
Portanto, o comprimento do padrão plano é 1,625" + 2,625" + 0,475", o que equivale a 4,725". Portanto, se você somar o comprimento plano de todos os flanges e adicionar uma tolerância de curvatura para cada área de curvatura, terá o comprimento plano correto da peça.
Agora, observe o desenho com mais atenção. Em projetos de chapas metálicas reais, as dimensões são normalmente atribuídas à intersecção dos flanges — isso é conhecido como Linha de Molde. Por isso, você deve subtrair o dobro da espessura do material mais o raio de curvatura do total para contabilizar cada área de curvatura. Esse valor é chamado de Recuo. Nesses casos, usar a Compensação de Curvatura costuma ser mais simples. A Compensação de Curvatura permite usar as dimensões da Linha de Molde para cada flange e, em seguida, ajustar o total adicionando um valor de compensação por curvatura. Aqui, a compensação é de -0,275, então 5" se torna 4,725" após a subtração.
Definições:
Tolerância de curvatura = Ângulo * (π / 180) * (Raio + Fator K * Espessura)
Compensação de curvatura = Tolerância de curvatura – (2 * Recuo)
Recuo interno = tan (Ângulo / 2) * Raio externo
Recuo = tan (Ângulo / 2) * (Raio + Espessura)
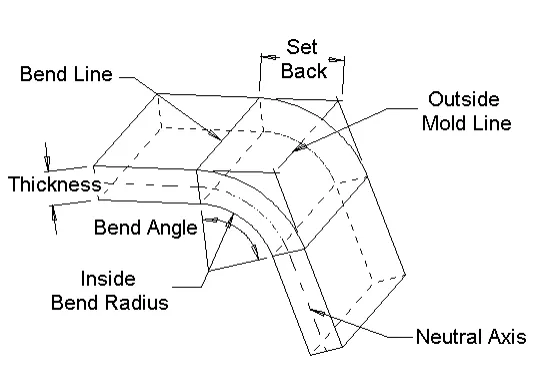
Tolerância de curvatura – O comprimento do arco através da área de curvatura no eixo neutro.
Ângulo de curvatura – O ângulo incluído do arco formado pela operação de dobra.
Compensação de curvatura – A quantidade em que o material é esticado ou comprimido pela operação de dobra. Todo o estiramento ou compressão ocorre na área de dobra.
Linhas de Curvatura – As linhas retas nas superfícies interna e externa do material onde o limite do flange encontra a área de dobra.
Raio de curvatura interno – O raio do arco na superfície interna da área de curvatura.
Fator K – Define a localização do eixo neutro. É medido como a distância do interior do material ao eixo neutro dividida pela espessura do material.
Linhas de Moldes – Para curvas inferiores a 180 graus, as linhas do molde são as linhas retas onde as superfícies do flange que delimitam a área da curva se cruzam. Isso ocorre tanto na superfície interna quanto na externa da curva.
Eixo Neutro – Observando a seção transversal da curva, o eixo neutro é o local teórico em que o material não é comprimido nem esticado.
Recuar – Para curvas menores que 180 graus, o recuo é a distância das linhas de curvatura até a linha do molde.
Como calcular o fator “K”:
Que eu saiba, não existe uma fórmula para calcular o fator k. Ah, tenho certeza de que em algum lugar algum engenheiro matemático tem uma fórmula. Mas provavelmente é complexa demais para a maioria de nós entender ou conseguir usar.
O fator k é a porcentagem da espessura do material onde não há alongamento ou compressão do material na área de dobra. Portanto, o eixo neutro!
Quanto mais duro o material, menor a compressão na parte interna da curva. Consequentemente, há mais alongamento na parte externa e o eixo neutro se move em direção à parte interna da curva. Materiais mais macios permitem maior compressão na parte interna e o eixo neutro permanece mais próximo do centro da espessura do material.
O raio de curvatura tem um efeito semelhante. Quanto menor o raio de curvatura, maior a necessidade de compressão, e o eixo neutro se move em direção à parte interna da curva. Em um raio maior, o eixo neutro permanece próximo ao centro da espessura do material.
| Fatores K genéricos | Alumínio | Aço | |
| Raio | Materiais macios | Materiais médios | Materiais duros |
| Dobra de ar | |||
| 0 a espessura | 0.33 | 0.38 | 0.40 |
| Espessura até 3×espessura | 0.40 | 0.43 | 0.45 |
| Espessura maior que 3× | 0.50 | 0.50 | 0.50 |
| Fundo | |||
| 0 a espessura | 0.42 | 0.44 | 0.46 |
| Espessura até 3×espessura | 0.46 | 0.47 | 0.48 |
| Espessura maior que 3× | 0.50 | 0.50 | 0.50 |
| Cunhagem | |||
| 0 a espessura | 0.38 | 0.41 | 0.44 |
| Espessura até 3×espessura | 0.44 | 0.46 | 0.47 |
| Espessura maior que 3× | 0.50 | 0.50 | 0.50 |
A fórmula a seguir pode ser usada no lugar da tabela como uma boa aproximação do fator K para flexão de ar:
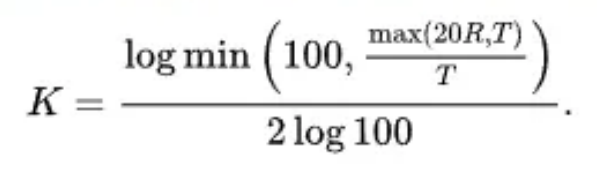
Diagrama e fórmulas de cálculo para tolerância de curvatura
Para ajudá-lo a dominar a fórmula de cálculo do comprimento de flexão desdobrado de forma mais simples e rápida, listamos quatro tabelas de coeficientes comuns, ilustramos dezesseis fórmulas de cálculo do comprimento de flexão desdobrado e também apresentamos alguns exemplos para melhor compreensão. Esperamos que o conteúdo a seguir possa ajudá-lo na prática. Em caso de dúvidas, entre em contato conosco.
| Largura da ranhura em V\espessura da placa | 0.6 | 0.8 | 1.0 | 1.2 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | Tamanho menor |
| V4 | 0.9 | 1.4 | 2.8 | ||||||||||
| V6 | 1.5 | 1.7 | 2.0 | 4.5 | |||||||||
| V7 | 1.8 | 2.1 | 2.4 | 5.0 | |||||||||
| V8 | 1.9 | 2.2 | 2.5 | 5.5 | |||||||||
| V10 | 2.1 | 2.3 | 2.7 | 7.0 | |||||||||
| V12 | 2.2 | 2.5 | 2.8 | 3.4 | 8.5 | ||||||||
| V14 | 3.5 | 3.8 | 6.4 | 6.8 | 10.0 | ||||||||
| V16 | 3.1 | 3.8 | 4.5 | 5.0 | 11.0 | ||||||||
| V18 | 3.3 | 4.0 | 13.0 | ||||||||||
| V20 | 4.0 | 4.9 | 5.1 | 6.6 | 7.2 | 7.8 | 14.0 | ||||||
| V25 | 4.4 | 5.0 | 5.5 | 6.8 | 7.8 | 8.3 | 16.5 | ||||||
| V32 | 5.0 | 5.5 | 6.1 | 8.7 |
Observação: Quando o tamanho gráfico da peça é marcado com tolerância negativa, o valor do fator de flexão pode ser aumentado, conforme mostrado na tabela, a parte vermelha pode ser aumentada para: 2,8; 2,82; 3,4; 3,43 ou 3,44: 4,5; 4,6; 5,5: 5,6
| Espessura mm\ângulo | Ranhura do molde largura | 90° | Canto interno | Forasteiro | 180° | ||
| 1.5 | V10 | 3.0 | 3.2 | 4.1 | 0.8 | ||
| 2.0 | V12 | 3.8 | 3.7 | 4.6 | 1.0 | ||
| 2.5 | V16 | 4.5 | 4.8 | 6.1 | 1.3 | ||
| Espessura mm\ângulo | 30° | 45° | 60° | 120° | 135° | 145° | |||||||||
| 1.0 | 0.35 | 0.7 | 1.1 | 1.0 | 0.6 | 0.4 | |||||||||
| 1.2 | 0.4 | 0.8 | 1.2 | 1.0 | 0.6 | 0.4 | |||||||||
| 1.5 | 0.5 | 1.0 | 1.6 | 1.4 | 0.9 | 0.6 | |||||||||
| 2.0 | 0.6 | 1.2 | 2.0 | 1.7 | 1.1 | 0.7 | |||||||||
| 2.5 | 0.8 | 1.6 | 2.6 | 2.2 | 1.4 | 0.85 | |||||||||
| 3.0 | 1.0 | 2.2 | 3.4 | 2.8 | 2.0 | 1.2 | |||||||||
| 4.0 | 3.7 | 2.4 | 1.4 | ||||||||||||
| Espessura mm | 0.5 | 1.0 | 1.2 | 1.5 | 2.0 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | |||||
| Furo de processo mm | 1. Sem buracos 2.Pode abrir buraco φ2 | φ2 | φ2,5 | φ3,0 | φ3,5 | φ4,0 | φ5,5 | φ6,0 | φ7,0 | ||||||
Observação: Se necessidades especiais forem permitidas, uma abertura maior pode ser usada.
Diagrama e fórmula de cálculo para uma curva
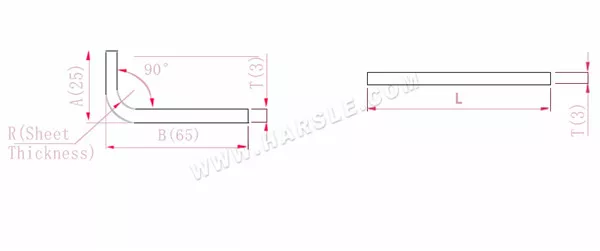
A, B — comprimento de curvatura da peça de trabalho
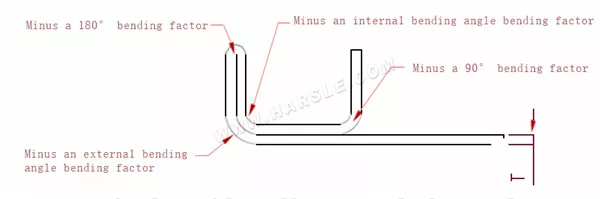
P' — coeficiente de flexão da borda (fator de flexão: um fator menos uma curvatura)
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
O comprimento expandido L=A+B-P', que é L=25+65-5,5=84,5
De acordo com a Tabela 1, a espessura da placa é 3, a matriz inferior é V25 e o coeficiente de flexão é 5,5
Nota: De acordo com a Tabela 1, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapa são diferentes.
Diagrama e fórmula de cálculo de duas dobras
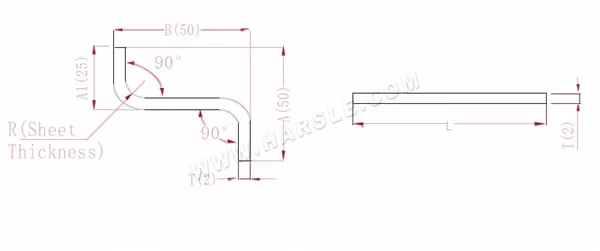
A(A1), B— comprimento de curvatura da peça de trabalho
P' — coeficiente de flexão da borda (fator de flexão: um fator menos uma curvatura)
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
O comprimento expandido L=A+T+B-2*P', que é L=50+2+50-2*3,4=95,2
De acordo com a Tabela 1, a espessura da placa é 2, a matriz inferior é V12 e o coeficiente de flexão é 3,4
Nota: De acordo com a Tabela 1, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapa são diferentes.
Diagrama e fórmula de cálculo de três dobras

A(A1), B (B1)-comprimento de curvatura da peça de trabalho
P' — coeficiente de flexão da borda (fator de flexão: um fator menos uma curvatura)
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
O comprimento expandido L=A+T+B+T-3*P', que é L=50+2+90+2-3*3,4=133,8
De acordo com a Tabela 1, a espessura da placa é 2, a matriz inferior é V12 e o coeficiente de flexão é 3,4
Nota: De acordo com a Tabela 1, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapa são diferentes.
Diagrama e fórmula de cálculo de quatro dobras
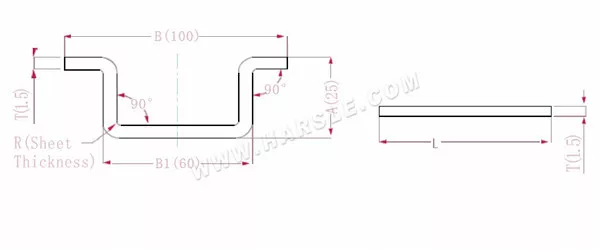
A, B (B1) - comprimento de curvatura da peça de trabalho
P' — coeficiente de flexão da borda (fator de flexão: um fator menos uma curvatura)
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
O comprimento expandido L=A+A+B+T+T-4*P', que é l = 25+25+100+1,5+1,5-4 * 2,8 = 141,8
De acordo com a Tabela 1, a espessura da chapa é 1,5, a matriz inferior é V12 e o coeficiente de flexão é 2,8
Nota: De acordo com a Tabela 1, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapa são diferentes.
Diagrama e fórmula de cálculo de seis curvas
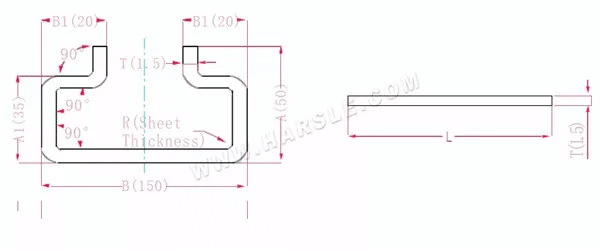
A(A1), B (B1)-comprimento de curvatura da peça de trabalho
P' — coeficiente de flexão da borda (fator de flexão: um fator menos uma curvatura)
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
O comprimento de expansão L=A+T+A+T+B+B1+B1-6*P'
que é l = 50+1,5+50+1,5+150+20+20-6 * 2,8 = 276,2
De acordo com a Tabela 1, a espessura da chapa é 1,5, a matriz inferior é V12 e o coeficiente de flexão é 2,8
Nota: De acordo com a Tabela 1, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapa são diferentes.
Diagrama e fórmula de cálculo de flexão de 180 graus
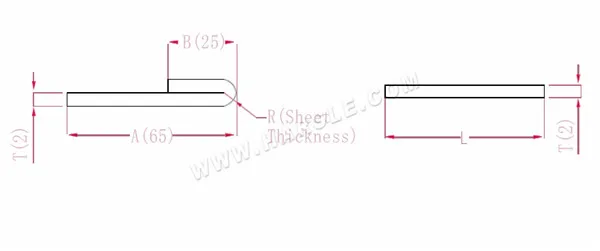
A, B — comprimento de curvatura da peça de trabalho
P'—coeficiente de flexão do filete de achatamento
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
O comprimento expandido L=A+B-P', que é L=25+65-1=89
De acordo com a Tabela 2, a espessura da chapa é 2, a matriz inferior é V12 e o fator de flexão é metade da espessura da chapa
Nota: De acordo com a Tabela 2, a seleção de diferentes matrizes inferiores tem diferentes coeficientes de curvatura e diferentes espessuras de chapa.
Diagrama e fórmula de cálculo de flexão de camada dupla
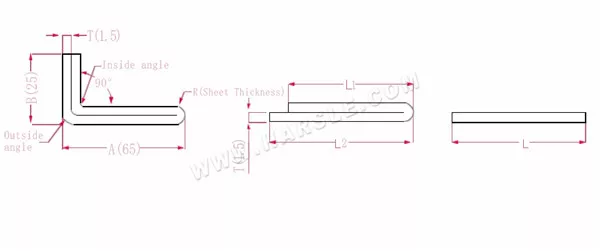
A, B — comprimento de curvatura da peça de trabalho
P1— coeficiente de flexão do canto interno
P2— coeficiente de flexão do ângulo de flexão externo
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
O comprimento expandido L1=(A-1,5) +(B-1,5)-P1, que é L1= (65-1,5) +(25-1,5)-3,2=83,8
L2=A+B-P2, que é L2=65+25-4,1=85,9
L=L1+L2-T/2, que é L=83,8+85,9-0,75=168,95
De acordo com a Tabela 2, a espessura da chapa é 1,5, a matriz inferior é V12, o coeficiente de curvatura do canto interno é 3,2, o coeficiente de curvatura do canto externo é 4,1 e o coeficiente de curvatura de 180 é 0,75.
Nota: De acordo com a Tabela 2, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapas são diferentes.
Diagrama e fórmula de cálculo de dobra de camada dupla com uma aresta
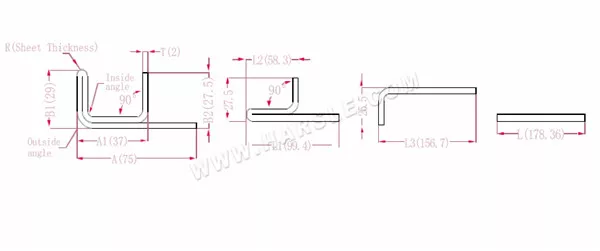
A, A1, A2, B1, B2, L, L1, L2, L3 — comprimento de curvatura da peça de trabalho
P1— coeficiente de flexão do canto interno
P2— coeficiente de flexão do ângulo de flexão externo
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
O comprimento expandido L1=(A1-T) +(B2-T)-P1 que é L1= (35-2) +(34-2)-3,7=61,3
L2=(B1-T) +(A2-T)-P1, que é L2= (50-2) +(34-2)-3,7=76,3
L3=A+B1+B2-2*P2, que é L3=70+35+50-2*4,6+145,8
L=L1+L2+L3-2*P3, que é L=61,3+75,3+145,8-2*1=280,4
De acordo com a Tabela 2, a espessura da chapa é 2, a matriz inferior é V12, o coeficiente de curvatura do canto interno é 3,7, o coeficiente de curvatura do canto externo é 4,6 e o coeficiente de curvatura de 90 é 1.
Nota: De acordo com a Tabela 2, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapas são diferentes.
Diagrama e fórmula de cálculo de dobra de camada dupla com duas arestas
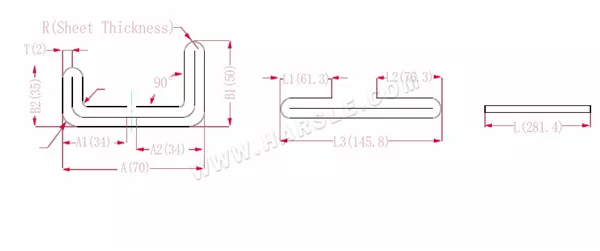
A, A1, A2, B1, B2, L, L1, L2, L3 — comprimento de curvatura da peça de trabalho
P1— coeficiente de flexão do canto interno
P2— coeficiente de flexão do ângulo de flexão externo
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
O comprimento expandido L1=(A1-T) +(B2-T)-P1 que é L1= (35-2) +(34-2)-3,7=61,3
L2=(B1-T) +(A2-T)-P1, que é L2= (50-2) +(34-2)-3,7=76,3
L3=A+B1+B2-2*P2, que é L3=70+35+50-2*4,6+145,8
L=L1+L2+L3-2*P3, que é L=61,3+75,3+145,8-2*1=280,4
De acordo com a Tabela 2, a espessura da chapa é 2, a matriz inferior é V12, o coeficiente de curvatura do canto interno é 3,7, o coeficiente de curvatura do canto externo é 4,6 e o coeficiente de curvatura de 90 é 1.
Nota: De acordo com a Tabela 2, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapas são diferentes.
Diagrama e fórmula de cálculo da flexão em degrau

A, B — comprimento de curvatura da peça de trabalho
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
Comprimento desdobrado L=A+1
Nota: Quando o degrau for igual à espessura de duas placas, adicione 0,5 para cada degrau e 1 para cada degrau.
Diagrama e fórmula de cálculo do ângulo especial de flexão 1
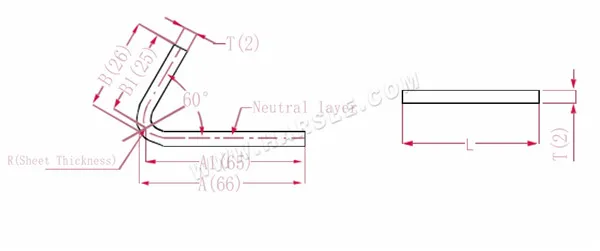
A(A1), B (B1)-comprimento de curvatura da peça de trabalho
P' — coeficiente de flexão da borda (fator de flexão: um fator menos uma curvatura)
R—curvatura e filete (geralmente espessura da chapa)
T— espessura do material
O comprimento de expansão L=(AT) +(BT)-P', que é L= (66-1) +(26-1)-2=65+25-2=88
De acordo com a Tabela 3, a espessura da chapa é 2, a matriz inferior é V12 e o coeficiente de flexão 60 é 2
Nota: De acordo com a Tabela 3, a camada neutra é selecionada como comprimento e largura de curvatura.
Diagrama e fórmula de cálculo do ângulo especial de flexão 2
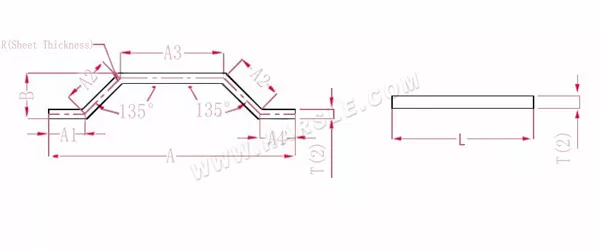
A (A1, A2, A3, A4), B— comprimento de curvatura da peça de trabalho
P — fator de flexão de 135 ângulos de flexão
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
O comprimento de expansão L = A1+A2+A3+A2+A4-PP.
Nota: a mesma flexão do passo de pressão só precisa reduzir dois coeficientes
De acordo com a Tabela 3: a espessura da chapa é 2, a matriz inferior é V12 e o coeficiente de flexão em 135 é 1,1.
Diagrama e fórmula de cálculo do ângulo especial de flexão 3

A (A1, A2), B (B1, B2) - comprimento de curvatura da peça de trabalho
P1—coeficiente de flexão de 120°
P2—coeficiente de flexão de 145°
P3—coeficiente de flexão de 90°
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
Observação: se o tamanho do gráfico estiver marcado na forma, o tamanho da forma deverá ser convertido para o tamanho da camada neutra ao calcular o comprimento de desdobramento;
O comprimento de expansão L=A11+B11+B21+A21-P1-P2-P3, que é l = 80+50+103+70-1,7-0,7-3,4 = 297,2
De acordo com a Tabela 3: a espessura da placa é 2, a matriz inferior é V12, o coeficiente de flexão de 120 é 1,7, o coeficiente de flexão de 145 é 0,7 e o coeficiente de flexão de 90 é 3,4
Nota: De acordo com a Tabela 3, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapa são diferentes.
Diagrama e fórmula de cálculo da ligação comum 1
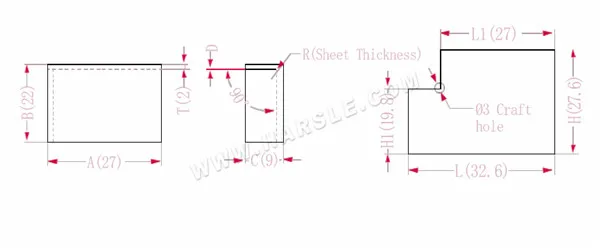
A, B, C — comprimento, largura e altura da aresta de dobra da peça de trabalho
P— coeficiente de flexão
R— curvatura e filete (geralmente espessura da chapa)
H(H1), l (L1) - o comprimento desdobrado de cada lado
T— espessura do material
D— folga do processo de dobra (geralmente 0~0,5)
O comprimento expandido L1=A, que é L1=27
L=A+CP, que é L=27+9-3,4=32,6
H1=BTD, ou seja, H1=22-2-0,2=19,8. Observação: D é 0,2.
H=B+CP, que é H=22+9-3,4=27,6
De acordo com a Tabela 1: a espessura da chapa é 2, a matriz inferior é V12 e o coeficiente de flexão é 3,4
Nota: De acordo com a Tabela 1, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapa são diferentes.
Diagrama e fórmula de cálculo da ligação comum 2
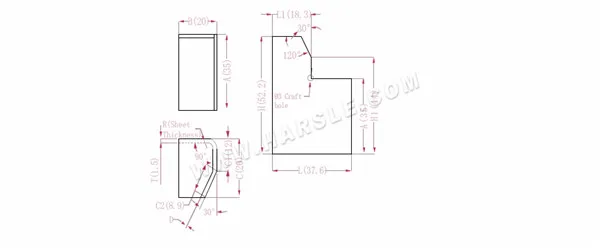
A, B, C — comprimento, largura e altura da aresta de dobra da peça de trabalho
H(H1), L (L1) - o comprimento desdobrado de cada lado
P—coeficiente de flexão de 90° P1—coeficiente de flexão de 30°
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
D— folga do processo de dobra (geralmente 0~0,5)
O comprimento expandido L1=BTD, que é L1=20-1,5-0,2=18,3
L=B+C1+C2-P-P1, que é L=20+12+8,9-2,8-0,5=37,6
H1=C1+APD, que é H1=12+35-2,8-0,2=44. Nota: D é 0,2.
H=A+CP, que é H=35+20-2,8=52,2
De acordo com a Tabela 1: a espessura da placa é 1,5, a matriz inferior é V12, o coeficiente de flexão é 2,8 e o coeficiente de flexão 30 é 0,5
Nota: De acordo com a Tabela 1, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapa são diferentes.
Diagrama e fórmula de cálculo da ligação comum 3
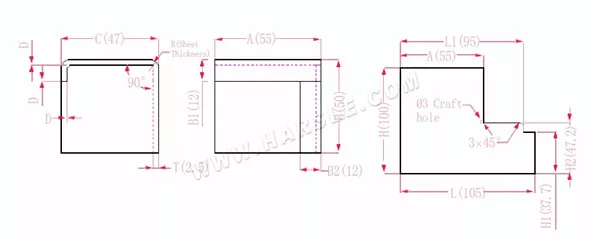
A, B, C — comprimento, largura e altura da aresta de dobra da peça de trabalho
H(H1), L (L1) - o comprimento desdobrado de cada lado
P— coeficiente de flexão
R— curvatura e filete (geralmente espessura da chapa)
T— espessura do material
D— folga do processo de dobra (geralmente 0~0,5)
O comprimento expandido H1=B-B1-D, que é H1=50-12-0,3=37,7. Observação: D é 0,2.
H2=BTD que é H2=50-2,5-0,3=47,2
H=B+C+B1-2*P, que é H=50+47+12-2*4,5=100
L1=A+CTDP, que é L1=55+47-2,5-0,3-4,5=94,7
L=A+C+B2-2*P, que é L=55+47+12-2*4,5=105
De acordo com a Tabela 1: a espessura da chapa é 1,5, a matriz inferior é V16 e o coeficiente de flexão é 4,5
Nota: De acordo com a Tabela 1, diferentes coeficientes de flexão de matrizes inferiores e diferentes espessuras de chapa são diferentes.










America-Miami-Customer-Feeback-1.jpg)
Uzbekistan-Customer-Feedback1.png)
Kosovo-Customer-Feedback11.png)
Russia-Customer-Feedback.jpg)
Russia-Customer-Feedback-3.jpg)






