Guida al calcolo della tolleranza di piegatura per presse piegatrici

Calcolare il corretto layout del modello piatto è fondamentale per ottenere una parte finita di buona qualità dal tuo pressa piegatriceEppure, molti programmatori CAD e CNC non hanno idea di come calcolare i valori richiesti. Anni fa, i veri esperti creavano dei foglietti riassuntivi e li appendevano al muro. Insegnavano ai nuovi apprendisti solo come applicare i risultati mostrati sul foglietto, non come calcolare i numeri. Bene, ora quegli esperti sono in pensione ed è tempo che una nuova generazione impari il modo giusto per calcolare il corretto layout del modello piatto. Puoi anche usare il nostro calcolatore della tolleranza di curvatura O calcolatrice di deduzione della curva per ottenere facilmente i risultati.
Calcolare la lunghezza del modello piatto a partire dal pezzo 3D non è poi così difficile. Anche se potresti trovare diverse formule che affermano di... calcolare il Tolleranza di piegatura (vedere Definizioni di piegatura): di solito si basano sulla stessa formula, semplificata inserendo l'angolo o un fattore K. Ah, e sì, è necessario conoscere il fattore K per calcolare la tolleranza di piegatura.
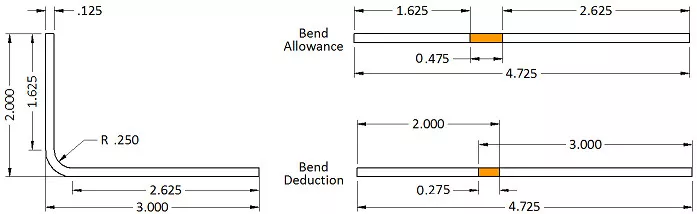
Prendiamo come esempio una semplice staffa a L. Ha due gambe, una da 5 cm e l'altra da 7,5 cm, con uno spessore del materiale di 3,25 cm e un raggio di curvatura interno di 6,35 cm. L'angolo di curvatura è di 90 gradi. Per trovare la lunghezza piana, non si misura dalla superficie interna o esterna, ma si considera l'asse neutro. È qui che entra in gioco il fattore K. Il fattore K rappresenta la posizione dell'asse neutro come percentuale dello spessore del materiale. Per questo calcolo, useremo un fattore K di 0,42 per determinare la tolleranza di curvatura e la forma piana corrette.
La formula (vedere Formule di flessione) è:
Tolleranza di piegatura = Angolo * (π / 180) * (Raggio + Fattore K * Spessore).
Inserendo i nostri numeri, abbiamo: tolleranza di piegatura = 90 * (π / 180) * (0,250 + 0,42 * 0,125) = 0,475″
Quindi la lunghezza del modello piatto è 1,625" + 2,625" + 0,475", che equivale a 4,725". Quindi, se si somma la lunghezza piatta di tutte le flange e si aggiunge una tolleranza di piegatura per ogni area di piegatura, si ottiene la lunghezza piatta corretta del pezzo.
Ora osserviamo più da vicino il disegno. Nella progettazione di lamiere nel mondo reale, le quote vengono in genere assegnate all'intersezione delle flange, nota come linea di stampo. Per questo motivo, è necessario sottrarre dal totale il doppio dello spessore del materiale più il raggio di piega per tenere conto di ciascuna area di piega. Questo valore è chiamato Setback. In questi casi, utilizzare la compensazione di piega è spesso più semplice. La compensazione di piega consente di utilizzare le quote della linea di stampo per ciascuna flangia, quindi di regolare il totale aggiungendo un valore di compensazione per piega. In questo caso, la compensazione è -0,275, quindi 5" diventano 4,725" dopo la sottrazione.
Definizioni:
Tolleranza di piegatura = Angolo * (π / 180) * (Raggio + Fattore K * Spessore)
Compensazione della piega = Tolleranza della piega – (2 * Arretramento)
Arretramento interno = tan (Angolo / 2) * Raggio esterno
Arretramento = tan (Angolo / 2) * (Raggio + Spessore)
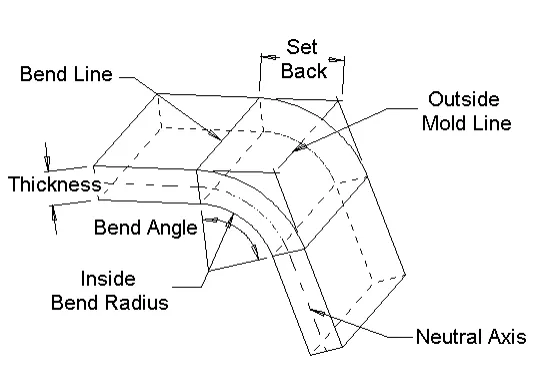
tolleranza di piegatura – La lunghezza dell'arco attraverso l'area di piegatura sull'asse neutro.
Angolo di piegatura – L’angolo compreso nell’arco formato dall’operazione di piegatura.
Compensazione della piega – L'entità dell'allungamento o della compressione del materiale durante l'operazione di piegatura. Si presume che tutto l'allungamento o la compressione avvengano nell'area di piegatura.
Linee di piegatura – Le linee rette sulle superfici interna ed esterna del materiale dove il confine della flangia incontra l'area di piegatura.
Raggio di curvatura interno – Il raggio dell’arco sulla superficie interna dell’area di piegatura.
Fattore K – Definisce la posizione dell'asse neutro. Viene misurata come la distanza dall'interno del materiale all'asse neutro divisa per lo spessore del materiale.
Linee di stampaggio – Per curve inferiori a 180 gradi, le linee di formatura sono le linee rette in cui si intersecano le superfici della flangia che delimitano l'area di piegatura. Ciò si verifica sia sulla superficie interna che su quella esterna della piega.
Asse neutro – Osservando la sezione trasversale della curva, l’asse neutro è il punto teorico in cui il materiale non viene né compresso né allungato.
Arretramento – Per curve inferiori a 180 gradi, l'arretramento è la distanza tra le linee di piegatura e la linea di stampo.
Come calcolare il fattore “K”:
A mia conoscenza, non esiste una formula per calcolare il fattore k. Oh, sono certo che da qualche parte qualche ingegnere matematico ne abbia una. Ma è molto probabilmente troppo complessa perché la maggior parte di noi possa capirla o usarla.
Il fattore k è la percentuale dello spessore del materiale in cui non si verifica allungamento o compressione del materiale nell'area di piegatura. Quindi, l'asse neutro!
Più duro è il materiale, minore è la compressione all'interno della curva. Pertanto, maggiore è l'allungamento all'esterno e l'asse neutro si sposta verso l'interno della curva. I materiali più morbidi consentono una maggiore compressione all'interno e l'asse neutro rimane più vicino al centro dello spessore del materiale.
Il raggio di curvatura ha un effetto simile. Minore è il raggio di curvatura, maggiore è la necessità di compressione e l'asse neutro si sposta verso l'interno della curva. Con un raggio maggiore, l'asse neutro rimane vicino al centro dello spessore del materiale.
| Fattori K generici | Alluminio | Acciaio | |
| Raggio | Materiali morbidi | Materiali medi | Materiali duri |
| piegatura in aria | |||
| da 0 a spessore | 0.33 | 0.38 | 0.40 |
| Spessore fino a 3×spessore | 0.40 | 0.43 | 0.45 |
| Maggiore di 3 volte lo spessore | 0.50 | 0.50 | 0.50 |
| Toccando il fondo | |||
| da 0 a spessore | 0.42 | 0.44 | 0.46 |
| Spessore fino a 3×spessore | 0.46 | 0.47 | 0.48 |
| Maggiore di 3 volte lo spessore | 0.50 | 0.50 | 0.50 |
| Coniazione | |||
| da 0 a spessore | 0.38 | 0.41 | 0.44 |
| Spessore fino a 3×spessore | 0.44 | 0.46 | 0.47 |
| Maggiore di 3 volte lo spessore | 0.50 | 0.50 | 0.50 |
La seguente formula può essere utilizzata al posto della tabella come buona approssimazione del fattore K per la flessione in aria:
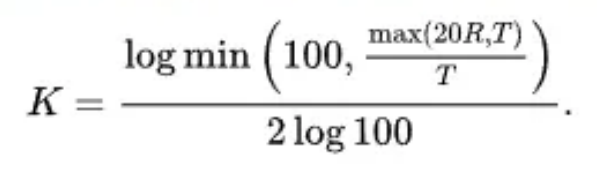
Diagramma e formule di calcolo per la tolleranza di curvatura
Per aiutarvi a padroneggiare la formula di calcolo della lunghezza di piegatura a riposo in modo più semplice e rapido, abbiamo elencato quattro tabelle di coefficienti comuni, illustrato sedici formule di calcolo della lunghezza di piegatura a riposo e fornito alcuni esempi per una migliore comprensione. Spero che i seguenti contenuti possano aiutarvi concretamente. Per qualsiasi domanda, non esitate a contattarci.
| Larghezza scanalatura a V\spessore piastra | 0.6 | 0.8 | 1.0 | 1.2 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | Dimensione più corta |
| V4 | 0.9 | 1.4 | 2.8 | ||||||||||
| V6 | 1.5 | 1.7 | 2.0 | 4.5 | |||||||||
| V7 | 1.8 | 2.1 | 2.4 | 5.0 | |||||||||
| V8 | 1.9 | 2.2 | 2.5 | 5.5 | |||||||||
| V10 | 2.1 | 2.3 | 2.7 | 7.0 | |||||||||
| V12 | 2.2 | 2.5 | 2.8 | 3.4 | 8.5 | ||||||||
| V14 | 3.5 | 3.8 | 6.4 | 6.8 | 10.0 | ||||||||
| V16 | 3.1 | 3.8 | 4.5 | 5.0 | 11.0 | ||||||||
| V18 | 3.3 | 4.0 | 13.0 | ||||||||||
| V20 | 4.0 | 4.9 | 5.1 | 6.6 | 7.2 | 7.8 | 14.0 | ||||||
| V25 | 4.4 | 5.0 | 5.5 | 6.8 | 7.8 | 8.3 | 16.5 | ||||||
| V32 | 5.0 | 5.5 | 6.1 | 8.7 |
Nota: Quando la dimensione grafica della parte è contrassegnata con tolleranza negativa, il valore del fattore di piegatura può essere aumentato, come mostrato nella tabella, la parte rossa può essere aumentata a: 2,8; 2,82; 3,4; 3,43 o 3,44: 4,5; 4,6; 5,5: 5,6
| Spessore mm\angolo | Scanalatura dello stampo larghezza | 90° | Angolo interno | Angolo esterno | 180° | ||
| 1.5 | V10 | 3.0 | 3.2 | 4.1 | 0.8 | ||
| 2.0 | V12 | 3.8 | 3.7 | 4.6 | 1.0 | ||
| 2.5 | V16 | 4.5 | 4.8 | 6.1 | 1.3 | ||
| Spessore mm\angolo | 30° | 45° | 60° | 120° | 135° | 145° | |||||||||
| 1.0 | 0.35 | 0.7 | 1.1 | 1.0 | 0.6 | 0.4 | |||||||||
| 1.2 | 0.4 | 0.8 | 1.2 | 1.0 | 0.6 | 0.4 | |||||||||
| 1.5 | 0.5 | 1.0 | 1.6 | 1.4 | 0.9 | 0.6 | |||||||||
| 2.0 | 0.6 | 1.2 | 2.0 | 1.7 | 1.1 | 0.7 | |||||||||
| 2.5 | 0.8 | 1.6 | 2.6 | 2.2 | 1.4 | 0.85 | |||||||||
| 3.0 | 1.0 | 2.2 | 3.4 | 2.8 | 2.0 | 1.2 | |||||||||
| 4.0 | 3.7 | 2.4 | 1.4 | ||||||||||||
| Spessore mm | 0.5 | 1.0 | 1.2 | 1.5 | 2.0 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | |||||
| Foro di processo mm | 1. Nessun foro 2. Può aprire il foro φ2 | φ2 | φ2.5 | φ3.0 | φ3.5 | φ4.0 | φ5.5 | φ6.0 | φ7.0 | ||||||
Nota: Se sono ammesse esigenze particolari, è possibile utilizzare un grado di apertura maggiore.
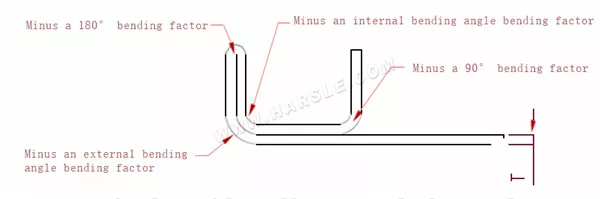
Diagramma e formula di calcolo per una curva
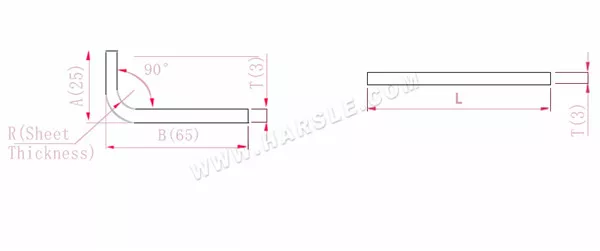
A, B— lunghezza di piegatura del pezzo in lavorazione
P'—coefficiente di flessione della flessione del bordo (fattore di flessione: un fattore meno una piega)
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
La lunghezza espansa L=A+B-P', che è L=25+65-5,5=84,5
Secondo la Tabella 1, lo spessore della piastra è 3, la matrice inferiore è V25 e il coefficiente di flessione è 5,5
Nota: secondo la Tabella 1, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.
Diagramma e formula di calcolo della curva a due pieghe
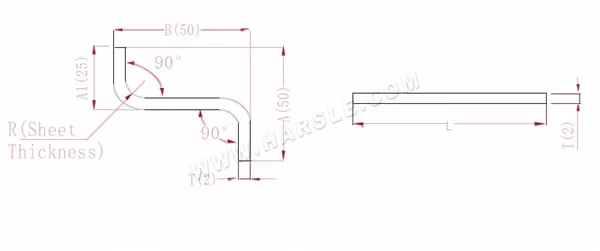
A(A1), B— lunghezza di piegatura del pezzo
P'—coefficiente di flessione della flessione del bordo (fattore di flessione: un fattore meno una piega)
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
La lunghezza espansa L=A+T+B-2*P', che è L=50+2+50-2*3.4=95.2
Secondo la Tabella 1, lo spessore della piastra è 2, la matrice inferiore è V12 e il coefficiente di flessione è 3,4
Nota: secondo la Tabella 1, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.
Diagramma e formula di calcolo della curva a tre pieghe

A(A1), B (B1)-lunghezza di piegatura del pezzo
P'—coefficiente di flessione della flessione del bordo (fattore di flessione: un fattore meno una piega)
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
La lunghezza espansa L=A+T+B+T-3*P', che è L=50+2+90+2-3*3.4=133.8
Secondo la Tabella 1, lo spessore della piastra è 2, la matrice inferiore è V12 e il coefficiente di flessione è 3,4
Nota: secondo la Tabella 1, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.
Diagramma e formula di calcolo della curva a quattro pieghe
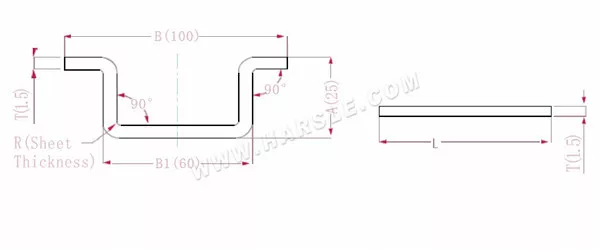
A, B (B1) - lunghezza di piegatura del pezzo
P'—coefficiente di flessione della flessione del bordo (fattore di flessione: un fattore meno una piega)
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
La lunghezza espansa L=A+A+B+T+T-4*P', che è l = 25+25+100+1,5+1,5-4 * 2,8 = 141,8
Secondo la Tabella 1, lo spessore della piastra è 1,5, la matrice inferiore è V12 e il coefficiente di flessione è 2,8
Nota: secondo la Tabella 1, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.
Diagramma e formula di calcolo della curva a sei pieghe
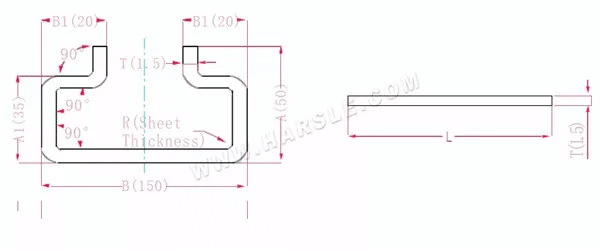
A(A1), B (B1)-lunghezza di piegatura del pezzo
P'—coefficiente di flessione della flessione del bordo (fattore di flessione: un fattore meno una piega)
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
La lunghezza di espansione L=A+T+A+T+B+B1+B1-6*P'
che è l = 50+1,5+50+1,5+150+20+20-6 * 2,8 = 276,2
Secondo la Tabella 1, lo spessore della piastra è 1,5, la matrice inferiore è V12 e il coefficiente di flessione è 2,8
Nota: secondo la Tabella 1, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.
Diagramma e formula di calcolo della flessione di 180 gradi
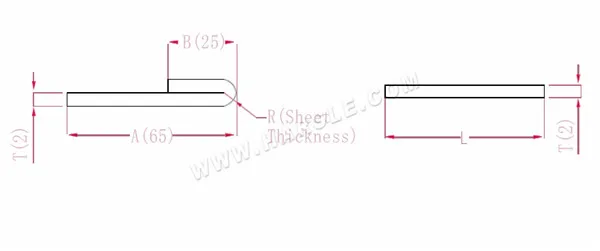
A, B— lunghezza di piegatura del pezzo in lavorazione
P'—coefficiente di flessione del raccordo di appiattimento
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
La lunghezza espansa L=A+B-P', che è L=25+65-1=89
Secondo la Tabella 2, lo spessore della piastra è 2, la matrice inferiore è V12 e il fattore di flessione è la metà dello spessore della piastra
Nota: secondo la Tabella 2, la selezione di diversi stampi inferiori presenta diversi coefficienti di flessione e diversi spessori della piastra.
Diagramma e formula di calcolo della flessione a doppio strato
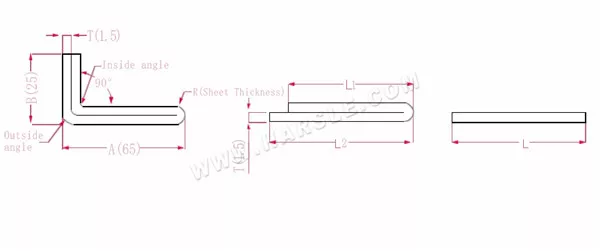
A, B— lunghezza di piegatura del pezzo in lavorazione
P1— coefficiente di flessione dell'angolo interno
P2— coefficiente di flessione dell'angolo di flessione esterno
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
La lunghezza espansa L1=(A-1.5) +(B-1.5)-P1, che è L1= (65-1.5) +(25-1.5)-3.2=83.8
L2=A+B-P2, che è L2=65+25-4.1=85.9
L=L1+L2-T/2, che è L=83,8+85,9-0,75=168,95
Secondo la Tabella 2, lo spessore della piastra è 1,5, la matrice inferiore è V12, il coefficiente di flessione dell'angolo interno è 3,2, il coefficiente di flessione dell'angolo esterno è 4,1 e il coefficiente di flessione 180 è 0,75.
Nota: secondo la Tabella 2, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.
Diagramma e formula di calcolo della piegatura a doppio strato con un bordo
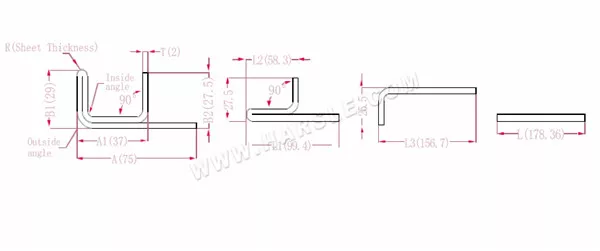
A, A1, A2, B1, B2, L, L1, L2, L3— lunghezza di piegatura del pezzo in lavorazione
P1— coefficiente di flessione dell'angolo interno
P2— coefficiente di flessione dell'angolo di flessione esterno
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
La lunghezza espansa L1=(A1-T) +(B2-T)-P1 che è L1= (35-2) +(34-2)-3.7=61.3
L2=(B1-T) +(A2-T)-P1, che è L2= (50-2) +(34-2)-3.7=76.3
L3=A+B1+B2-2*P2, che è L3=70+35+50-2*4.6+145.8
L=L1+L2+L3-2*P3, che è L=61,3+75,3+145,8-2*1=280,4
Secondo la Tabella 2, lo spessore della piastra è 2, la matrice inferiore è V12, il coefficiente di flessione dell'angolo interno è 3,7, il coefficiente di flessione dell'angolo esterno è 4,6 e il coefficiente di flessione a 90° è 1.
Nota: secondo la Tabella 2, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.
Diagramma e formula di calcolo della piegatura a doppio strato con due bordi
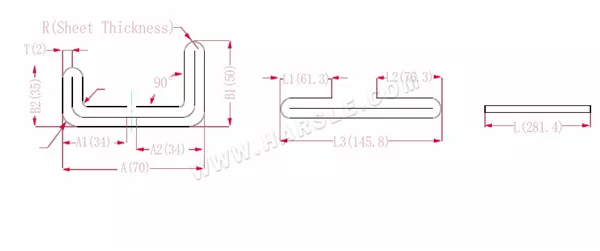
A, A1, A2, B1, B2, L, L1, L2, L3— lunghezza di piegatura del pezzo in lavorazione
P1— coefficiente di flessione dell'angolo interno
P2— coefficiente di flessione dell'angolo di flessione esterno
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
La lunghezza espansa L1=(A1-T) +(B2-T)-P1 che è L1= (35-2) +(34-2)-3.7=61.3
L2=(B1-T) +(A2-T)-P1, che è L2= (50-2) +(34-2)-3.7=76.3
L3=A+B1+B2-2*P2, che è L3=70+35+50-2*4.6+145.8
L=L1+L2+L3-2*P3, che è L=61,3+75,3+145,8-2*1=280,4
Secondo la Tabella 2, lo spessore della piastra è 2, la matrice inferiore è V12, il coefficiente di flessione dell'angolo interno è 3,7, il coefficiente di flessione dell'angolo esterno è 4,6 e il coefficiente di flessione a 90° è 1.
Nota: secondo la Tabella 2, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.
Diagramma e formula di calcolo della flessione a gradini

A, B— lunghezza di piegatura del pezzo in lavorazione
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
Lunghezza non piegata L=A+1
Nota: quando il gradino è uguale allo spessore di due piastre, aggiungere 0,5 per ogni gradino e 1 per ogni gradino.
Diagramma e formula di calcolo dell'angolo di piegatura speciale 1
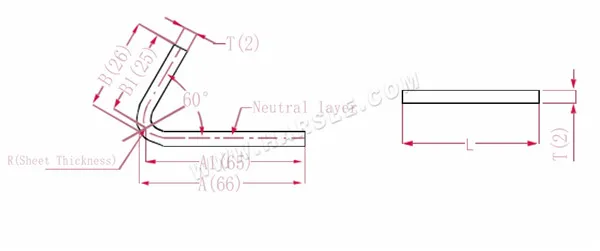
A(A1), B (B1)-lunghezza di piegatura del pezzo
P'—coefficiente di flessione della flessione del bordo (fattore di flessione: un fattore meno una piega)
R—piegatura e raccordo (generalmente spessore della piastra)
T— spessore del materiale
La lunghezza di espansione L=(AT) +(BT)-P', che è L= (66-1) +(26-1)-2=65+25-2=88
Secondo la Tabella 3, lo spessore della piastra è 2, la matrice inferiore è V12 e il coefficiente di flessione 60 è 2
Nota: secondo la Tabella 3, lo strato neutro viene selezionato come lunghezza e larghezza di piegatura.
Diagramma e formula di calcolo dell'angolo di piegatura speciale 2
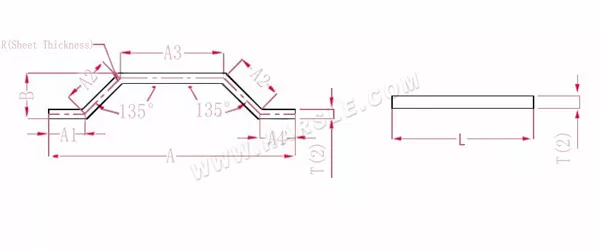
A (A1, A2, A3, A4), B— lunghezza di piegatura del pezzo
P— fattore di flessione di 135 angoli di flessione
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
La lunghezza di espansione L = A1+A2+A3+A2+A4-PP.
Nota: la stessa flessione a gradino di pressione deve ridurre solo due coefficienti
Secondo la Tabella 3: lo spessore della piastra è 2, la matrice inferiore è V12 e il coefficiente di flessione a 135 è 1,1.
Diagramma e formula di calcolo dell'angolo di piegatura speciale 3

A (A1, A2), B (B1, B2) - lunghezza di piegatura del pezzo
P1—coefficiente di flessione 120°
P2—coefficiente di flessione 145°
P3—coefficiente di flessione a 90°
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
Nota: se la dimensione grafica è contrassegnata sulla forma, la dimensione della forma deve essere convertita nella dimensione del livello neutro quando si calcola la lunghezza di sviluppo;
La lunghezza di espansione L=A11+B11+B21+A21-P1-P2-P3, che è l = 80+50+103+70-1,7-0,7-3,4 = 297,2
Secondo la Tabella 3: lo spessore della piastra è 2, la matrice inferiore è V12, il coefficiente di flessione 120 è 1,7, il coefficiente di flessione 145 è 0,7 e il coefficiente di flessione 90 è 3,4
Nota: secondo la Tabella 3, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.
Schema e formula di calcolo del legame comune 1
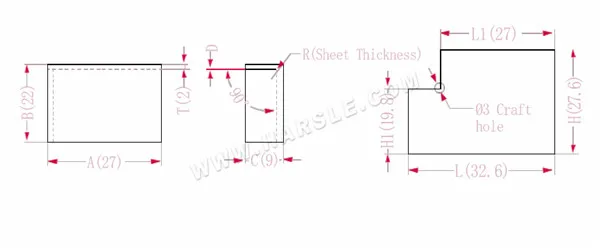
A, B, C: lunghezza, larghezza e altezza del bordo di piegatura del pezzo in lavorazione
P— coefficiente di flessione
R— piega e raccordo (generalmente spessore della piastra)
H(H1), l (L1)-la lunghezza dispiegata di ciascun lato
T— spessore del materiale
D— gioco del processo di piegatura (generalmente 0~0,5)
La lunghezza espansa L1=A, che è L1=27
L=A+CP, che è L=27+9-3.4=32.6
H1=BTD, ovvero H1=22-2-0,2=19,8. Nota: D è 0,2.
H=B+CP, che è H=22+9-3.4=27.6
Secondo la Tabella 1: lo spessore della piastra è 2, la matrice inferiore è V12 e il coefficiente di flessione è 3,4
Nota: secondo la Tabella 1, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.
Diagramma e formula di calcolo del legame comune 2
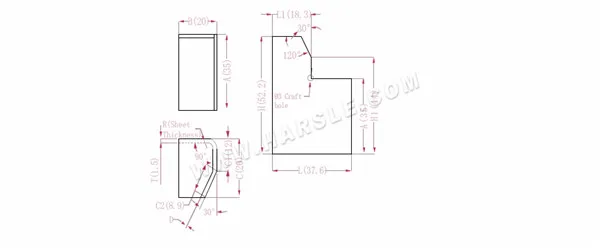
A, B, C: lunghezza, larghezza e altezza del bordo di piegatura del pezzo in lavorazione
H(H1), L(L1)-la lunghezza dispiegata di ciascun lato
P—coefficiente di flessione 90° P1—coefficiente di flessione 30°
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
D— gioco del processo di piegatura (generalmente 0~0,5)
La lunghezza espansa L1=BTD, che è L1=20-1,5-0,2=18,3
L=B+C1+C2-P-P1, che è L=20+12+8,9-2,8-0,5=37,6
H1=C1+APD, ovvero H1=12+35-2,8-0,2=44. Nota: D è 0,2.
H=A+CP, che è H=35+20-2.8=52.2
Secondo la Tabella 1: lo spessore della piastra è 1,5, la matrice inferiore è V12, il coefficiente di flessione è 2,8 e il coefficiente di flessione 30 è 0,5
Nota: secondo la Tabella 1, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.
Diagramma e formula di calcolo del legame comune 3
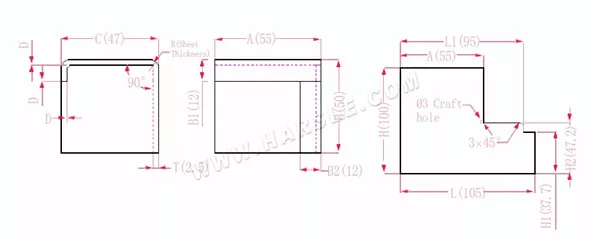
A, B, C: lunghezza, larghezza e altezza del bordo di piegatura del pezzo in lavorazione
H(H1), L(L1)-la lunghezza dispiegata di ciascun lato
P— coefficiente di flessione
R— piega e raccordo (generalmente spessore della piastra)
T— spessore del materiale
D— gioco del processo di piegatura (generalmente 0~0,5)
La lunghezza estesa H1=B-B1-D, ovvero H1=50-12-0,3=37,7. Nota: D è 0,2.
H2=BTD che è H2=50-2,5-0,3=47,2
H=B+C+B1-2*P, che è H=50+47+12-2*4.5=100
L1=A+CTDP, che è L1=55+47-2.5-0.3-4.5=94.7
L=A+C+B2-2*P, che è L=55+47+12-2*4.5=105
Secondo la Tabella 1: lo spessore della piastra è 1,5, la matrice inferiore è V16 e il coefficiente di flessione è 4,5
Nota: secondo la Tabella 1, i diversi coefficienti di flessione delle matrici inferiori e i diversi spessori delle piastre sono diversi.










America-Miami-Customer-Feeback-1.jpg)
Uzbekistan-Customer-Feedback1.png)
Kosovo-Customer-Feedback11.png)
Russia-Customer-Feedback.jpg)
Russia-Customer-Feedback-3.jpg)






