Lors de vos projets, il est crucial de comprendre l'importance de déterminer la longueur réelle d'un composant. Des mesures précises garantissent un assemblage parfait et un fonctionnement optimal des composants. Dans cet article, je partagerai des méthodes et des conseils pratiques que j'ai trouvés efficaces pour déterminer la longueur réelle de divers composants. Que vous soyez dans le secteur de la fabrication ou du bricolage, maîtriser cette compétence peut grandement améliorer votre précision et votre efficacité. Découvrons ensemble les meilleures pratiques pour obtenir des mesures précises !

Dans le traitement de tôle On rencontre souvent des pièces de formes diverses, telles que des tuyaux de ventilation, des joints déformés, etc. Pour finaliser leur usinage, la tôle doit d'abord être dépliée : la surface de l'objet est étalée sur un plan selon sa forme et ses dimensions réelles. Le dépliage de la tôle est une étape préparatoire à l'usinage. tôle Matériau, condition préalable à l'usinage correct des pièces en tôle. Pour dessiner correctement un schéma de dépliage de tôle, il est nécessaire de connaître les dimensions réelles du schéma ou celles de ses composants. Lorsque la surface tridimensionnelle de la ligne et la surface de projection ne sont pas parallèles, la longueur réelle du dessin projeté est altérée. Il est donc nécessaire d'utiliser une méthode graphique avant le dépliage pour déterminer la longueur réelle du segment de ligne.

Les méthodes permettant de déterminer la longueur réelle d'un segment de droite comprennent la méthode de la rotation, la méthode du triangle rectangle, la méthode du trapèze rectangle et la méthode du plan de projection auxiliaire. La maîtrise et l'application de ces méthodes constituent une condition préalable et fondamentale à l'acquisition des compétences en dépliage de tôles.

La méthode de rotation

La méthode de rotation consiste à faire pivoter une ligne inclinée autour d'un axe perpendiculaire à un plan de projection jusqu'à une position parallèle à un autre plan de projection, le segment de droite projeté sur ce plan de projection correspondant à la longueur réelle de la ligne inclinée. Pour des raisons de commodité graphique, l'axe passe généralement par l'une des extrémités de la ligne inclinée, l'extrémité étant le centre du cercle et la ligne inclinée correspondant au rayon de rotation.

Principe de rotation pour une longueur réelle : le schéma ci-dessous illustre le principe de rotation pour une longueur réelle. ab est une droite de position générale, inclinée par rapport à tout plan de projection. Les projections a'b' de ab sur le plan V et sur le plan H sont toutes deux plus courtes que la longueur réelle. En supposant que l'axe AO soit perpendiculaire au plan H à une extrémité de AB, lorsque AB est tourné autour de l'axe AO jusqu'à une position AB1 parallèle au plan V, sa projection a'b1' sur le plan V (la ligne pointillée sur le schéma indique la longueur réelle) reflétera sa longueur réelle.

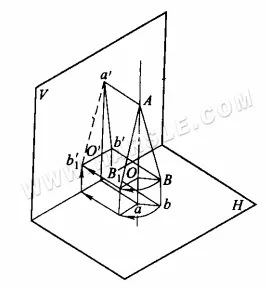
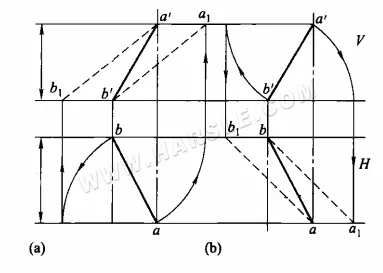
Méthode de rotation pour les longueurs réelles : Le schéma ci-dessous illustre la méthode spécifique d'utilisation de la méthode de rotation pour les longueurs réelles. Dans le schéma ci-dessous (a), la projection horizontale ab est tournée de manière à être parallèle à la projection orthogonale, ce qui donne les points a1 et b1, reliant a1b' ou a'b1, qui est la longueur réelle du segment AB ; dans le schéma ci-dessous (b), la projection orthogonale a'b' est tournée de manière à être parallèle à la projection horizontale, ce qui donne les points a1 et b1, reliant a1b ou ab1, qui est la longueur réelle du segment AB.

Exemple : Le schéma ci-dessous illustre la longueur réelle du prisme d'un prisme oblique par rotation. La projection montre que la base du prisme oblique est parallèle au plan horizontal et que sa projection horizontale reflète sa forme solide et sa longueur réelle. Les quatre faces restantes (côtés) sont deux ensembles de triangles, dont les projections ne reflètent pas la forme réelle. Pour obtenir la forme réelle de ces deux ensembles de triangles, il faut trouver la longueur réelle de leurs prismes. La forme étant symétrique d'avant en arrière, seules les longueurs réelles des deux prismes latéraux sont nécessaires pour tracer le schéma.

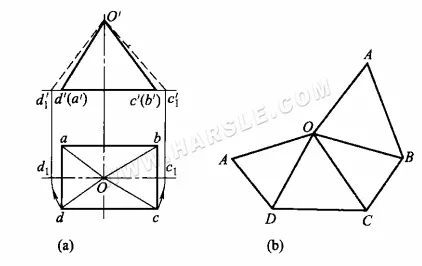
Les étapes spécifiques de la création d'un diagramme de dépliage sont les suivantes

1. Utilisez la méthode de rotation pour trouver les longueurs réelles des nervures latérales Oc et Od. Comme indiqué dans le schéma ci-dessous, prenez O comme centre du cercle, respectivement Oc, Od comme rayon de rotation, croisez la ligne horizontale en c1, d1. c1, d1 de c1, d1 jusqu'à la ligne verticale, et la projection orthographique c'd' ligne d'extension intersectée en c1'd1′, reliant O'c1′, O'd1′ est la longueur réelle du prisme latéral Oc et Od.

2. Tracez une droite AD de longueur égale à ad à l'emplacement approprié sur le diagramme, puis tracez △AOD avec A et D comme centres du cercle et Od' comme rayon de l'arc, coupant en O ; tracez ensuite un arc avec O comme centre du cercle et Oc1′ comme rayon, coupant l'arc réalisé avec D comme centre et dc comme rayon en C. Reliez OC et DC pour obtenir △DOC. Tracez les deux côtés restants de △COB et △BOA de la même manière pour obtenir un cône trigonal dont les côtés sont élargis.

La figure ci-dessous est un cône tronqué, la longueur réelle du cône et l'expansion, doit d'abord dessiner le sommet du cône, devenir un cône complet, puis faire une série de surfaces de cône, et utiliser la méthode de rotation pour trouver ces lignes ont été tronquées une partie de la longueur réelle de la ligne (également disponible pour laisser une partie de la longueur réelle de la ligne), vous pouvez faire l'expansion de la figure.

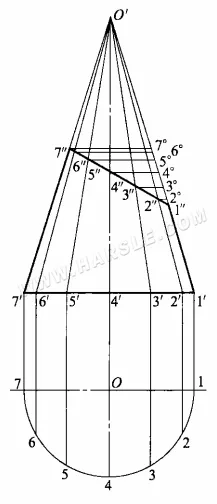
Pour trouver la longueur réelle de la partie tronquée de la ligne, les étapes de création du diagramme sont les suivantes.

1. Prolongez la ligne de forme 1'1″ et 7'7″ jusqu'à ce qu'elles se croisent, ce qui donne le sommet du cône O'.

2. Faites le cercle de base du cône, et divisez la circonférence du cercle de base en un certain nombre de parties égales (ici 1/2 la circonférence du cercle de base est divisée en 6 parties égales), pour obtenir des parties égales 1, 2, …, 7, de chaque point égal à la vue principale de la verticale, et la projection orthogonale du cercle de base intersectée aux points 1′, 2′, …, 7′, puis de chaque point et du sommet du cône O' pour la ligne, pour obtenir le cône les lignes de la surface conique.

3. Parmi les lignes du cône, seules les lignes de contour 1″1′ et 7″7′ sont parallèles à la projection orthogonale et reflètent sa longueur, tandis que les autres ne reflètent pas sa longueur réelle. La méthode consiste à tracer une ligne parallèle de 7'1′ à partir de 7″, 6″…, 2″ et à couper la ligne de contour O'1′ à 7°, 6°,…, 2°, O'6°, O'5°,…, O'2° pour O'6″, O'5″,…, O' 2″ respectivement. 2″ de longueur réelle.

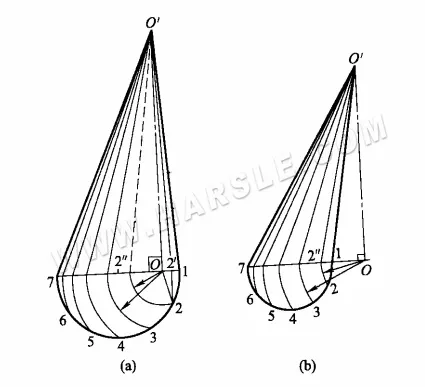
Le schéma ci-dessus montre la longueur réelle du cône oblique par rotation. Les étapes sont les suivantes.

1. Tout d'abord, divisez la moitié du cercle de base, la circonférence du cercle de base en un certain nombre de parties égales (dans le schéma en 6 parties égales).

2. avec le pied vertical O comme centre du cercle, O1, O2, …, O6 pour le rayon de l'arc, et 1 ~ 7 intersection de ligne à 2″ et ainsi de suite sur chaque point.

3. Tracez une droite reliant les points 2″ etc. à O', O'2′ etc. étant la longueur réelle de la droite passant par les équinoxes. Autrement dit, O'2′ est la projection orthogonale de la droite O2 et O'2″ est la longueur réelle de cette droite.

Le diagramme ci-dessous montre les longueurs réelles des prismes d'un joint carré en utilisant la méthode de rotation et en les développant.

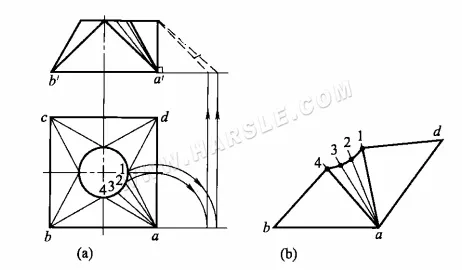
Les étapes pour dessiner les longueurs réelles des prismes sont

1. Dessinez la vue principale et la vue de dessus, égalisez l'ouverture du cercle de la vue de dessus et connectez les lignes simples correspondantes.

2. faites pivoter les lignes simples a1, (a4), a2, (a3) et tracez des lignes verticales vers le haut pour dériver leurs longueurs réelles a-1, (a-4) et a-2, (a-3) sur le côté droit de la vue principale.

3. En utilisant les longueurs réelles des lignes simples, les longueurs des bords de la bouche carrée et les longueurs d'arc équivalentes de la bouche ronde, dessinez les étalements 1/4 à tour de rôle.

Lorsque la partie de transition du tube carré est opposée au tube rond, un joint carré-rond doit être réalisé. L'embouchure carrée peut être carrée ou rectangulaire, et l'embouchure ronde peut être centrale, latérale ou dans un angle. La forme de ces joints peut donc varier, mais la méthode de détermination de la longueur réelle des joints carrés et ronds est fondamentalement la même.

Méthode du triangle rectangle

La méthode du triangle rectangle est une méthode couramment utilisée pour trouver la longueur réelle.

Principe de la méthode du triangle rectangle et méthode de tracé : le schéma suivant (a) est le schéma de principe de la méthode du triangle rectangle pour les longueurs réelles. Le segment AB n'est pas parallèle au plan de projection, et ses projections ab et a'b' ne reflètent pas la longueur réelle. Dans le plan ABba, une droite est parallèle à ab passant par le point A et coupe Bb au point B1, ce qui donne le triangle rectangle ABB1. Dans ce triangle, la longueur réelle de l'hypoténuse AB du triangle rectangle peut être déterminée en connaissant les longueurs des deux côtés rectangles AB1 et BB1. Les longueurs de AB1 et BB1 sont trouvées sur le schéma de projection comme AB1 = ab, BB1 = b'b1′, ou BB1 = b'bx – a'ax. La connaissance de ces deux côtés rectangles permet de tracer de manière unique le triangle rectangle recherché.

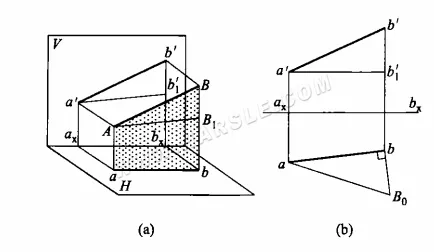
La figure (b) ci-dessus illustre l'utilisation de la méthode du triangle rectangle pour trouver la longueur réelle. La projection de la droite AB est connue sous les noms de ab et a'b'. Pour trouver la longueur réelle AB, vous pouvez d'abord tracer une droite horizontale passant par le point a', croiser la droite bb' au point b1', bb1' étant la longueur d'un côté à angle droit du segment. Ensuite, la vue de dessus de l'ab pour un autre côté à angle droit, au-dessus du point b, est une droite verticale et intercepte bB0 = b'b1', connectée à aB0, c'est-à-dire la longueur réelle du segment.

Exemple : Le schéma ci-dessous montre un petit et un grand joint de bouche carré, essayez de trouver la longueur réelle de sa ligne principale AC et de sa ligne auxiliaire BC.

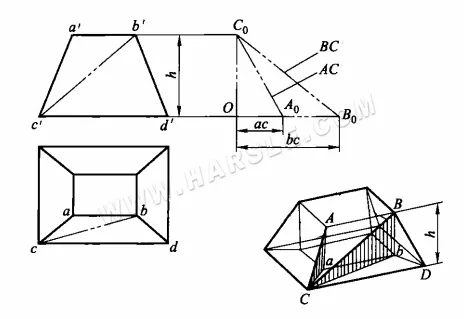
On peut voir sur le schéma que la longueur réelle AC se trouve dans un triangle rectangle dont les côtés sont aC et Aa, tandis que la longueur réelle BC se trouve dans le triangle rectangle BbC. Dans les deux triangles, Aa = Bb = h, qui est égale à la hauteur de l'articulation. Les deux autres côtés rectangles, aC et bC, sont respectivement égaux aux projections ac et bc de AC et BC en vue de dessus. Ainsi, les longueurs réelles de AC et BC peuvent être trouvées comme suit.

1. faire un angle droit B0OC0.

2. intercepter OA0 et OB0 sur le côté horizontal de cet angle droit respectivement égal à ac et bc dans la vue de dessus, et intercepter OC0 sur le côté vertical égal à la hauteur h dans la vue principale.

3. connectez C0A0 et C0B0, alors les hypoténuses C0A0 et C0B0 sont les longueurs réelles des AC et BC demandés.

La méthode du trapèze rectangle

La méthode du trapèze à angle droit est également une méthode courante pour trouver des longueurs réelles.

Principe de la méthode du trapèze rectangle pour les longueurs réelles et méthode de tracé : le schéma suivant illustre le principe de la méthode du trapèze rectangle pour les longueurs réelles. La position générale de la droite AB sur les surfaces V et H ne reflète pas la longueur réelle, mais les deux extrémités de la droite AB et la distance entre les surfaces V (Aa et Bb) peuvent être obtenues sur la surface H. Les mêmes points (A, B) et la distance entre les surfaces H peuvent également être obtenues sur la surface V (Aa et Bb). Selon ce principe, la longueur réelle de la droite AB peut être déterminée par la méthode du trapèze rectangle. Il existe deux méthodes spécifiques pour représenter graphiquement les longueurs réelles.

1. en utilisant la projection orthographique de la longueur réelle de la ligne AB : la projection orthographique de AB a'b' comme bord inférieur du trapèze rectangle, à partir de a', b' deux points respectivement vers le haut de la ligne verticale, intercepte la longueur de Aa', Bb', connectée à AB, c'est-à-dire pour la demande.

2. est l'utilisation de la projection horizontale de la longueur réelle du segment de droite AB : la projection horizontale de AB comme bord inférieur d'un trapèze rectangle, à partir de a, b deux points respectivement vers le haut de la ligne verticale, intercepter la longueur de Aa, Bb, relier AB qui est la demande.

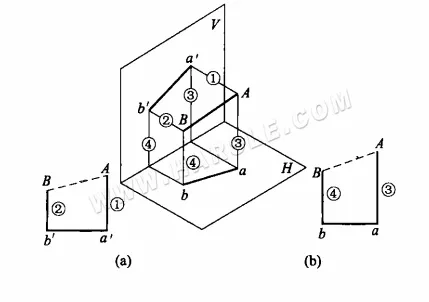
Exemple : La figure suivante montre une articulation de déformation en fer à cheval, ses bouches supérieure et inférieure sont des cercles, mais les deux cercles ne sont pas parallèles et ne sont pas égaux en diamètre, essayez de faire une méthode de trapèze à angle droit de sa longueur de ligne et de son diagramme d'expansion.

La figure (a) ci-dessus montre que, comme sa surface n'est pas conique, pour réaliser son diagramme de développement, il suffit d'utiliser la droite reliant la surface à un certain nombre de triangles, puis de trouver la forme réelle de ces triangles un par un. La procédure graphique est la suivante.

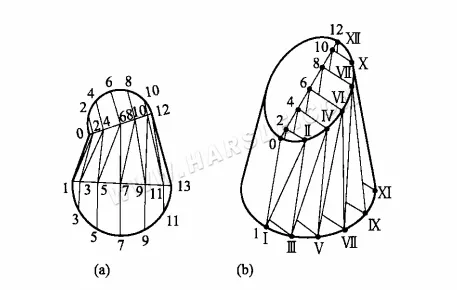
1. Faites 12 parties égales des bouches supérieure et inférieure et divisez la surface en 24 triangles comme indiqué sur le schéma.

2. Trouvez les longueurs réelles des droites Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII, puis tracez la forme réelle de la série de triangles.

Dans de tels exemples, si la méthode de rotation ou la méthode du triangle rectangle est utilisée pour déterminer la longueur réelle, il est nécessaire de projeter le segment de droite sur la vue de dessus. Comme la surface supérieure de la déformation en fer à cheval et le plan de projection horizontal sont inclinés, la surface supérieure de la vue de dessus est reflétée comme une ellipse. Ces deux méthodes d'extension de la carte sont évidemment plus complexes ; il est donc préférable d'utiliser la méthode du trapèze rectangle.

Comme dans la figure (b) ci-dessus, la surface pliée Ⅰ-1-Ⅱ-2-Ⅲ-3…XII-12 s'étend sur la figure ci-dessous, puis sur la figure au-dessus de la ligne de pliage Ⅰ-Ⅱ-Ⅲ…XII, c'est-à-dire les longueurs réelles Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII, et ainsi de suite. Cette méthode de recherche des longueurs réelles est la méthode du trapèze rectangle.

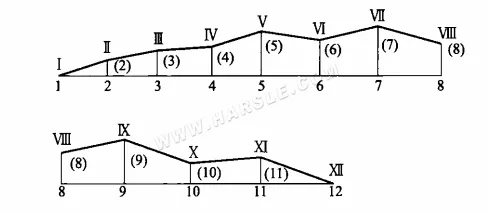
Comme le montre la méthode de représentation graphique, la méthode du trapèze rectangle repose également sur la projection d'une droite inclinée comme base, dont la distance entre les deux extrémités de la droite inclinée et le même plan de projection est égale à celle des deux côtés de l'angle droit. Après avoir formé un trapèze rectangle, on calcule l'hypoténuse de ce trapèze, c'est-à-dire la longueur réelle de la droite souhaitée. Le triangle rectangle peut être considéré comme un cas particulier de la méthode du trapèze rectangle, où la longueur du côté rectangle est nulle.

La méthode ci-dessus permet d'obtenir les deux lignes latérales de chaque triangle sur la surface du joint de déformation en fer à cheval, dont l'autre côté correspond à la longueur des ouvertures circulaires supérieure et inférieure, égale à l'arc déplié. De cette manière, une série de triangles peut être formée par la méthode des triangles à trois côtés connus, disposés de manière à obtenir le schéma suivant du joint de déformation en fer à cheval.

Méthode de changement de visage

En plus des méthodes ci-dessus pour trouver la longueur réelle de la ligne, il existe également la méthode courante consistant à modifier la surface.

Principe de la méthode de modification de la surface pour la longueur réelle et méthode de dessin : le principe de la méthode de modification de la surface consiste à conserver le segment spatial inchangé, à créer une nouvelle surface de projection pour le rendre parallèle au segment demandé et perpendiculaire à l'original. La projection du segment sur la nouvelle surface de projection reflétera sa longueur réelle. Le schéma ci-dessus illustre la longueur réelle d'un segment de droite.

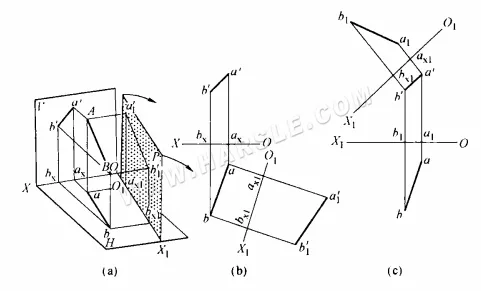
Comme le montre le schéma ci-dessus (a), le segment AB n'est pas parallèle aux plans de projection H et V et sa projection ne reflète pas la longueur réelle. La nouvelle projection a1'b1' reflète la longueur réelle de AB. Une analyse plus approfondie de l'espace représenté dans la figure (a) ci-dessus révèle les relations de projection suivantes pour la méthode des changements de surface.

1. Étant donné que la nouvelle surface de projection P est parallèle à AB et perpendiculaire au plan H, alors la ligne d'intersection entre la nouvelle surface de projection P et le plan H, O1X1 (appelée nouvel axe de projection), est nécessairement parallèle à la projection ab du plan H de la ligne AB, O1X1 // ab, telle que reflétée dans la projection du plan H.

2. Puisque les surfaces P et V sont simultanément perpendiculaires à la surface H, la distance de la projection a1'b1' de la surface P sur O1X1 et la distance de la projection a'b' de la surface V sur OX doivent refléter simultanément les distances perpendiculaires des deux extrémités A et B de la ligne spatiale à la surface H, et elles sont égales entre elles, a1ax1 = a'ax = Aa et b1'bx1 = Bb. Pour faciliter la désignation, la nouvelle projection parallèle à AB La projection a1'b1' qui reflète la longueur réelle est appelée la nouvelle projection, la projection a'b' qui ne reflétait pas initialement la longueur réelle est appelée l'ancienne projection ou projection de remplacement, et la projection du plan H qui leur est perpendiculaire en même temps est appelée la projection invariante. De cette façon, cette relation de projection pour la méthode de la surface de remplacement peut être exprimée comme la distance de la nouvelle projection au nouvel axe étant égale à la distance de l'ancienne projection à l'ancien axe.

3. Étant donné que les surfaces P et V sont perpendiculaires à la surface H, la connexion entre la projection P et la projection H en tout point de la ligne doit être perpendiculaire au nouvel axe de projection O1X1, la ligne entre la projection invariante et les anciennes et nouvelles projections est perpendiculaire aux axes de projection anciens et nouveaux respectivement, après dépliage.

Conformément à la relation de projection ci-dessus de la méthode de permutation, les étapes graphiques doivent être

1. comme indiqué dans (b) ci-dessus, faites en sorte que le nouvel axe de projection O1X1 soit parallèle à ab.

2. Tracez une ligne perpendiculaire passant par les points a et b jusqu'à l'axe O1X1 et coupez O1X1 aux points ax1 et bx1.

3. Déplacez les projections a' et b' du plan V vers l'axe OX vers le nouveau plan de projection, mesurez ax1a1'=axa' et bx1b1'=bxb' sur les lignes verticales.

4. Reliez les points a1′ et b1′, la nouvelle projection a1'b1′ de la ligne AB, qui reflète la longueur réelle de AB.

Exemple : Le diagramme ci-dessous montre l’utilisation de la méthode du plan de projection auxiliaire pour trouver la forme réelle d’une section cylindrique.

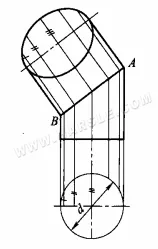
Les étapes du dessin sont les suivantes.

1. Créez une vue principale et une vue de dessus, en divisant la vue de dessus par 1/2 de la circonférence du cercle en 6 parties égales.

2. tracez une ligne verticale vers le haut à travers le point équidistant pour donner la position de la ligne principale dans la vue principale.

3. en traçant des perpendiculaires vers le bas à partir des points équidistants pour couper la ligne centrale inférieure, la largeur entre les lignes simples de la section

4. tracer des lignes perpendiculaires passant par l'intersection des lignes sur l'ouverture oblique de la section jusqu'à l'axe long parallèle à l'ouverture oblique de la section, puis tracer la distance entre les points équidistants dans la vue de dessus et la ligne centrale du cercle inférieur, à son tour, jusqu'aux points de la vue secondaire, conformément à la règle de « largeur égale ».

5. Reliez les points afin de créer une ellipse solide de la section.

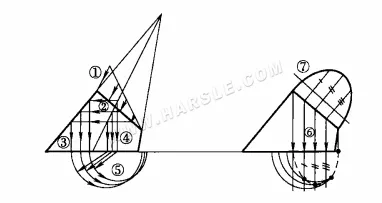
Le schéma ci-dessous illustre l'utilisation de la méthode du plan de projection auxiliaire pour déterminer la forme réelle de la section de l'orthocône. Les schémas ①, ②, … (7) indiquent l'ordre de tracé et les lignes de connexion.

En général, il n'est pas nécessaire de tracer des lignes sur la surface du cône pour obtenir la forme réelle de la section conique. Il est préférable d'utiliser la méthode du cercle de trame, comme illustré ci-dessus. Afin de clarifier les lignes, les trois étapes du diagramme seront dessinées séparément dans cet exemple ; le diagramme lui-même n'a pas besoin d'être séparé. Les étapes sont les suivantes.

1. Cercles de trame : la ligne de projection de la section est divisée en 6 parties égales ; la ligne horizontale des points égaux ci-dessus est coupée par la ligne de contour ; la ligne verticale est tracée vers le bas à partir de chaque point d'intersection sur la ligne de contour et coupée au bas du cône ; les cercles de trame sont tracés à leur tour avec le centre du cercle O, voir la figure (a) ci-dessus.

2. Vue de dessus de la section transversale : en traçant une ligne verticale vers le bas à travers chaque équivoque des lignes de section transversale dans la vue principale, en coupant le cercle de latitude correspondant, une série de points d'intersection est obtenue ; en reliant les points d'intersection, la projection de la vue de dessus de la section transversale peut être obtenue, voir la figure (b) ci-dessus.

3. Pour trouver la forme réelle de la section : tracez une ellipse parallèle à l'axe longitudinal de la section 1″7″ ; tracez des lignes perpendiculaires de chaque point égal de la section 1~7 à l'axe longitudinal 1″7″ ; conformément au principe d'égalité des largeurs, tracez une série de largeurs a, b, c, d et e de la section dans la vue de dessus sur la projection auxiliaire, ce qui donne des points de 2″, 3″, 4″, 5″ et 6″ ; reliez les points, c'est-à-dire la forme réelle de la section conique, voir le schéma (b) ci-dessus. Figure (c) ci-dessus.

Le diagramme ci-dessous montre l'utilisation de la méthode de surface de projection auxiliaire pour trouver la forme réelle de la section conique oblique.

L'utilisation de la vue auxiliaire pour la forme réelle d'une section conique oblique est similaire à celle d'une section conique orthogonale. Cependant, le cône oblique présente la particularité d'avoir son sommet incliné d'un côté et son axe également incliné, de sorte que le centre d'une série de cercles de trame ne se trouve pas au même point sur le même axe. Ainsi, au lieu de créer des cercles concentriques, on crée un cône avec un centre pour chaque cercle de trame. Cette caractéristique peut être maîtrisée en suivant les trois étapes décrites ci-dessus pour dessiner la vue auxiliaire d'une section solide.

Les étapes spécifiques du dessin sont les suivantes.

1. Pour le cercle de trame : la ligne de section 4 parties égales ; pour les points égaux de la ligne horizontale, croisant la ligne de contour ; de la ligne de contour sur les points jusqu'à la ligne verticale, croisant le cercle inférieur ; points égaux de la ligne horizontale et l'intersection de l'axe des points pour le cercle de trame du centre, du centre du cercle au cercle inférieur ; respectivement, le centre du cercle de trame et le rayon correspondant pour le cercle de trame.

2. La vue de dessus de la section : à travers la vue principale des lignes de section de chaque équivoque, des lignes verticales descendantes et l'intersection du cercle de latitude correspondant, résultant en une série de points d'intersection ; avec les points d'intersection, vous pouvez obtenir la vue de dessus de la projection de section.

3. Pour réaliser la forme réelle de la section : en fonction de la largeur de la forme de la section trouvée dans la vue de dessus, réalisez une vue auxiliaire 1/2 pour dessiner la forme réelle 1/2 de la section conique oblique.

Comparaison des méthodes de longueur réelle

Sur la base de l’analyse ci-dessus, une comparaison simple peut être faite entre les quatre méthodes de recherche de la longueur réelle d’une ligne réelle.

La méthode de rotation résout la longueur réelle en modifiant la position de la figure dans l'espace, sans modifier la position du plan de projection.

La méthode de permutation résout la longueur réelle en changeant la position du plan de projection sans changer la position de la figure.

La méthode du triangle rectangle et la méthode du trapèze rectangle (la méthode du triangle rectangle peut être considérée comme un cas particulier de la méthode du trapèze rectangle) résolvent la ligne de longueur réelle en ne changeant ni la position de la figure spatiale ni la position du plan de projection.