Quando si lavora su un progetto, comprendere l'importanza di determinare la lunghezza effettiva di un componente è fondamentale. Misurazioni accurate garantiscono che i componenti si incastrino perfettamente e funzionino come previsto. In questo articolo, condividerò metodi pratici e suggerimenti che ho trovato efficaci per determinare la lunghezza effettiva di vari componenti. Che si tratti di produzione o di progetti fai da te, padroneggiare questa abilità può migliorare notevolmente la precisione e l'efficienza. Approfondiamo le migliori pratiche per ottenere misurazioni accurate!

Nella lavorazione di lamiera parti, pezzi lavorati di varie forme si incontrano spesso, come tubi di ventilazione, giunti deformati, ecc. Per completare la loro lavorazione, la lamiera deve prima essere dispiegata, la superficie dell'oggetto viene distribuita su un piano in base alla sua forma e dimensione reali. Lo sviluppo della lamiera è un processo preparatorio per la lamiera materiale, ed è anche un prerequisito per la corretta lavorazione delle parti in lamiera. Per disegnare correttamente un diagramma di sviluppo della lamiera, è necessario conoscere le dimensioni effettive del diagramma di sviluppo o le dimensioni effettive dei componenti rilevanti del diagramma di sviluppo. Quando la superficie tridimensionale della linea e la superficie di proiezione non sono parallele, i disegni di progetto nella proiezione non riflettono la loro lunghezza reale, quindi prima dello sviluppo è necessario utilizzare un metodo grafico per scoprire la lunghezza reale del segmento di linea.

I metodi per calcolare la lunghezza reale di un segmento includono il metodo della rotazione, il metodo del triangolo rettangolo, il metodo del trapezio rettangolo e il metodo del piano di proiezione ausiliario. La padronanza e l'applicazione di questi metodi per calcolare la lunghezza reale di un segmento sono un prerequisito e una base per l'acquisizione delle competenze di sviluppo della lamiera.

Il metodo di rotazione

Il metodo di rotazione prevede la rotazione di una linea inclinata attorno a un asse perpendicolare a un piano di proiezione fino a una posizione parallela a un altro piano di proiezione, dove il segmento di linea proiettato su tale piano di proiezione è la lunghezza reale della linea inclinata. Per comodità grafica, l'asse passa generalmente per uno degli estremi della linea inclinata, il punto finale è il centro del cerchio e la linea inclinata è il raggio della rotazione.

Il principio di rotazione per lunghezze reali: il diagramma seguente mostra il principio di rotazione per lunghezze reali. ab è una retta di posizione generale, inclinata rispetto a qualsiasi piano di proiezione. La proiezione di ab a'b' sul piano V e la proiezione di ab sul piano H sono entrambe più corte della lunghezza reale. Supponendo che l'asse AO sia perpendicolare al piano H a un'estremità di AB, quando AB viene ruotato attorno all'asse AO in una posizione AB1 parallela al piano V, la sua proiezione a'b1′ sul piano V (la linea tratteggiata nel diagramma indica la lunghezza reale) rifletterà la sua lunghezza reale.

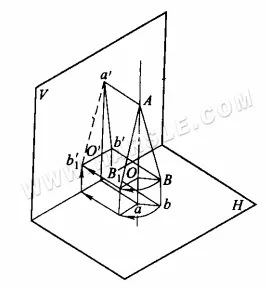
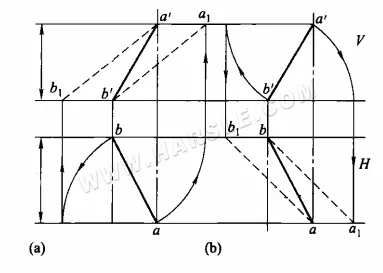
Metodo di rotazione per lunghezze reali: il diagramma seguente mostra il metodo specifico per utilizzare il metodo di rotazione per lunghezze reali. Nel diagramma seguente (a), la proiezione orizzontale ab viene ruotata in modo che sia parallela alla proiezione ortografica, ottenendo i punti a1 e b1, che collegano a1b' o a'b1, che è la lunghezza reale del segmento AB; nel diagramma seguente (b), la proiezione ortografica a'b' viene ruotata in modo che sia parallela alla proiezione orizzontale, ottenendo i punti a1 e b1, che collegano a1b o ab1, che è la lunghezza reale del segmento AB.

Esempio: il diagramma seguente mostra un diagramma della lunghezza reale del prisma di un prisma obliquo utilizzando il metodo di rotazione. Come si può vedere dalla proiezione, la base del prisma obliquo è parallela al piano orizzontale e la sua proiezione orizzontale riflette la sua forma solida e la sua lunghezza reale. Le quattro facce rimanenti (lati) sono due insiemi di triangoli, le cui proiezioni non riflettono la forma reale. Per ottenere la forma reale dei due insiemi di triangoli, è necessario trovare la lunghezza reale dei loro prismi. Poiché la forma è simmetrica da davanti a dietro, per disegnare il diagramma sono necessarie solo le lunghezze reali dei due prismi laterali.

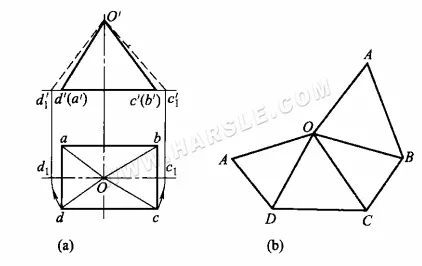
I passaggi specifici per realizzare un diagramma di sviluppo sono

1. Utilizzare il metodo di rotazione per trovare le lunghezze reali delle nervature laterali Oc e Od. Come mostrato nel diagramma sottostante, prendere O come centro del cerchio, rispettivamente Oc, Od come raggio di rotazione, intersecare la linea orizzontale in c1, d1. c1, d1 da c1, d1 lungo la linea verticale e la proiezione ortografica c'd', la linea di estensione intersecata in c1'd1′, che collega O'c1′, O'd1′, è la lunghezza reale del prisma laterale Oc e Od.

2. Traccia una linea AD di lunghezza pari ad ad nella posizione appropriata sul diagramma, quindi disegna △AOD con A e D come centro del cerchio e Od' come raggio dell'arco, intersecandolo in O; quindi traccia un arco con O come centro del cerchio e Oc1′ come raggio, intersecandolo con l'arco formato con D come centro e dc come raggio in C. Collega OC e DC per ottenere △DOC. Disegna i due lati rimanenti di △COB e △BOA allo stesso modo per ottenere un cono trigonale con i lati espansi.

La figura sottostante è un cono troncato, la lunghezza reale del cono e l'espansione, dovresti prima disegnare la parte superiore del cono, diventare un cono completo, quindi creare una serie di superfici coniche e utilizzare il metodo di rotazione per trovare queste linee che sono state troncate parte della lunghezza reale della linea (disponibile anche per lasciare parte della lunghezza reale della linea), puoi fare l'espansione della figura.

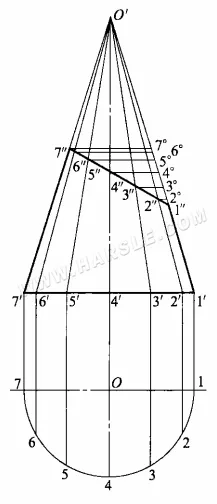
Per trovare la lunghezza reale della parte troncata della linea, i passaggi del diagramma sono i seguenti.

1. estendere la linea di forma di 1'1″ e 7'7″ per intersecarsi, ottenendo la parte superiore del cono O'.

2. Tracciare il cerchio di base del cono e dividere la circonferenza del cerchio di base in un numero di parti uguali (qui 1/2 della circonferenza del cerchio di base è divisa in 6 parti uguali), per ottenere le parti uguali 1, 2, …, 7, da ogni punto uguale alla vista principale della guida verticale e la proiezione ortogonale del cerchio di base intersecata nei punti 1′, 2′, …, 7′, e quindi da ogni punto e dalla sommità del cono O' per la linea, per ottenere il cono le linee della superficie conica.

3. Tra le linee del cono, solo le linee di contorno 1″1′ e 7″7′ sono parallele alla proiezione ortogonale e ne riflettono la lunghezza, mentre le altre non riflettono la lunghezza reale. Il metodo consiste nel tracciare una linea parallela di 7'1′ da 7″, 6″…, 2″ e intersecare la linea di contorno O'1′ a 7°, 6°,…, 2°, O'6°, O'5°,…, O'2° per O'6″, O'5″,…, O' 2″ rispettivamente. 2″ di lunghezza reale.

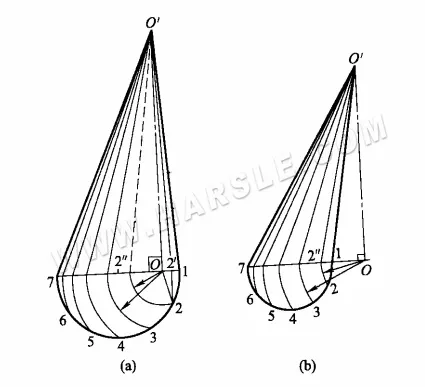
Il diagramma sopra mostra la lunghezza reale del cono obliquo in base alla rotazione. I passaggi sono i seguenti.

1. Per prima cosa, dividi la metà del cerchio di base, ovvero la circonferenza del cerchio di base in un numero di parti uguali (nel diagramma in 6 parti uguali).

2. con il piede verticale O come centro del cerchio, O1, O2, …, O6 per il raggio dell'arco e 1 ~ 7 intersezione delle linee a 2 "e così su ogni punto.

3. Traccia una linea dai punti 2″ ecc. a O', O'2′ ecc., essendo la lunghezza reale della linea che passa per gli equinozi. In altre parole, O'2′ è la proiezione ortogonale della linea O2 e O'2″ è la lunghezza reale della linea O2.

Il diagramma seguente mostra le lunghezze reali dei prismi di un giunto quadrato utilizzando il metodo di rotazione e dilatandoli.

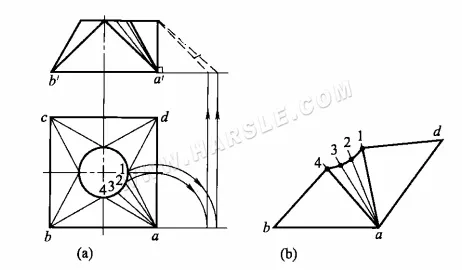
I passaggi per disegnare le lunghezze reali dei prismi sono

1. Disegna la vista principale e la vista dall'alto, equipara l'apertura del cerchio della vista dall'alto e collega le linee semplici corrispondenti.

2. ruotare le linee semplici a1, (a4), a2, (a3) e tracciare linee verticali verso l'alto per ricavare le loro lunghezze reali a-1, (a-4) e a-2, (a-3) sul lato destro della vista principale.

3. Utilizzando le lunghezze reali delle linee semplici, le lunghezze dei bordi della bocca quadrata e le lunghezze equivalenti degli archi della bocca rotonda, disegnare a turno le distribuzioni di 1/4.

Laddove la parte di transizione del tubo quadrato sia opposta al tubo tondo, deve esserci un giunto quadrato-tondo. L'imboccatura quadrata può essere quadrata o rettangolare, mentre l'imboccatura tonda può essere al centro, su un lato o su un angolo; pertanto, la forma di tali giunti può variare, ma il metodo per determinare la lunghezza effettiva dei giunti quadrati e tondi è sostanzialmente lo stesso.

Metodo del triangolo rettangolo

Il metodo del triangolo rettangolo è un metodo comunemente utilizzato per trovare la lunghezza reale.

Il principio del metodo del triangolo rettangolo e il metodo di disegno: il seguente diagramma (a) è il diagramma di principio del metodo del triangolo rettangolo per lunghezze reali. Il segmento AB non è parallelo al piano di proiezione e le sue proiezioni ab e a'b' non riflettono la lunghezza reale. Nel piano ABba, si traccia una retta parallela ad ab passante per A e che interseca Bb nel punto B1, dando origine al triangolo rettangolo ABB1. In questo triangolo, la lunghezza reale dell'ipotenusa AB del triangolo rettangolo può essere trovata conoscendo le lunghezze dei due cateti rettangoli AB1 e BB1. E le lunghezze di AB1 e BB1 si trovano sul diagramma di proiezione come AB1 = ab, BB1 = b'b1′, o BB1 = b'bx – a'ax. Conoscendo questi due cateti rettangoli si disegna in modo univoco il triangolo rettangolo cercato.

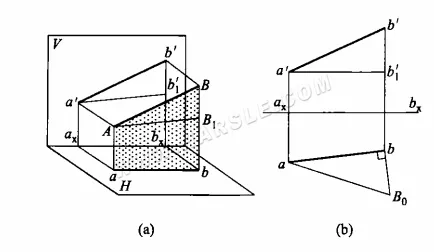
La figura (b) sopra mostra l'uso del metodo del triangolo rettangolo per trovare la lunghezza reale. La proiezione della retta AB è nota come ab e a'b'; per trovare la lunghezza reale di AB, si può prima tracciare una retta orizzontale passante per il punto a', incrociare la retta bb' nel punto b1′, bb1′, ovvero la lunghezza di un lato retto del segmento. Quindi, la vista dall'alto di ab per un altro lato retto, sopra il punto b, la retta verticale citata e l'intercetta bB0 = b'b1′, collegata ad aB0, ovvero la lunghezza reale del segmento.

Esempio: il diagramma seguente mostra un giunto a bocca quadrata piccolo e grande; provare a trovare la lunghezza reale della sua linea principale AC e della linea ausiliaria BC.

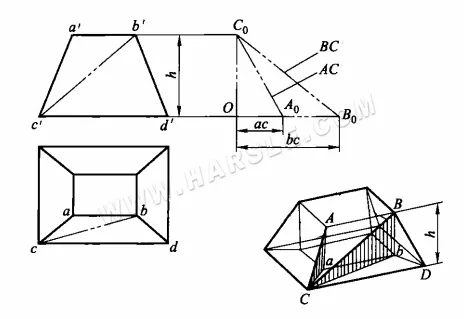
Dal diagramma si può vedere che la lunghezza reale AC può essere trovata in un triangolo rettangolo con aC e Aa come lati rettangoli, mentre la lunghezza reale BC può essere trovata nel triangolo rettangolo BbC. In entrambi i triangoli, Aa = Bb = h, che è uguale all'altezza del giunto. Gli altri due lati rettangoli aC e bC sono uguali alle proiezioni ac e bc di AC e BC rispettivamente nella vista dall'alto. In questo modo, le lunghezze reali di AC e BC possono essere trovate come segue.

1. creare un angolo retto B0OC0.

2. intercettare OA0 e OB0 sul lato orizzontale di quell'angolo retto rispettivamente pari ad ac e bc nella vista dall'alto, e intercettare OC0 sul lato verticale pari all'altezza h nella vista principale.

3. collega C0A0 e C0B0, quindi l'ipotenusa C0A0 e C0B0 sono le lunghezze reali di AC e BC richiesti.

Il metodo del trapezio ad angolo retto

Anche il metodo del trapezio ad angolo retto è un metodo comune per trovare lunghezze reali.

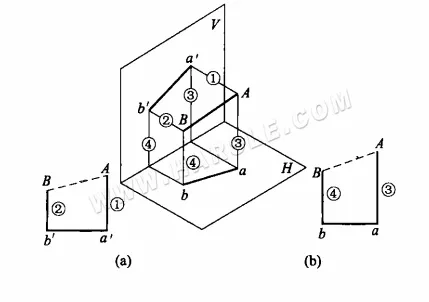
Il principio del metodo del trapezio ad angolo retto per la lunghezza reale e il metodo di disegno: il diagramma seguente mostra il principio di utilizzo del metodo del trapezio ad angolo retto per la lunghezza reale. La posizione generale della linea AB sulla superficie V e sulla superficie H non può riflettere la lunghezza reale, ma i due estremi della linea AB e la distanza tra la superficie V possono essere ottenuti sulla superficie H, ovvero Aa e Bb, gli stessi due punti A e B e la distanza tra la superficie H può essere ottenuta anche sulla superficie V, ovvero Aa e Bb. Sulla base di questo principio, la lunghezza reale della linea AB può essere trovata utilizzando il metodo del trapezio ad angolo retto. Esistono due metodi specifici per rappresentare graficamente le lunghezze reali.

1. utilizzando la proiezione ortografica della lunghezza reale della linea AB: la proiezione ortografica di AB a'b' come bordo inferiore del trapezio rettangolo, da a', b' due punti rispettivamente in alto sulla linea verticale, intercetta la lunghezza di Aa', Bb', collegata ad AB, cioè, per la richiesta.

2. è l'uso della proiezione orizzontale della lunghezza reale del segmento AB: la proiezione orizzontale di AB come bordo inferiore di un trapezio rettangolo, da a, b due punti rispettivamente in alto sulla linea verticale, intercetta la lunghezza di Aa, Bb, collega AB che è la lunghezza richiesta.

Esempio: la figura seguente mostra un giunto di deformazione a ferro di cavallo, la cui bocca superiore e inferiore sono cerchi, ma i due cerchi non sono paralleli e non hanno lo stesso diametro; provare a realizzare un metodo trapezio ad angolo retto della sua lunghezza di linea e del diagramma di espansione.

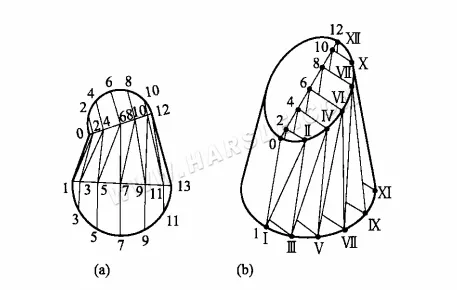
Dalla figura (a) sopra si può osservare che, poiché la sua superficie non è conica, per tracciare il diagramma di espansione è sufficiente usare la linea che va e viene dalla superficie in un certo numero di triangoli, e calcolarne la forma reale uno alla volta. I passaggi specifici per la rappresentazione grafica sono i seguenti.

1. Realizzare 12 parti uguali delle bocche superiore e inferiore e dividere la superficie in 24 triangoli come mostrato nel diagramma.

2. Trova le lunghezze reali delle linee Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII, quindi crea la forma reale della serie di triangoli.

Per tali esempi, se si utilizza il metodo di rotazione o il metodo del triangolo rettangolo per trovare la lunghezza reale, è necessario eseguire la proiezione del segmento sulla vista dall'alto. Poiché la superficie superiore del giunto di deformazione a ferro di cavallo e il piano di proiezione orizzontale sono inclinati, la superficie superiore nella vista dall'alto viene riflessa come un'ellisse. Ovviamente, questi due metodi per l'espansione della mappa sono più complessi; in questo caso, è opportuno utilizzare il metodo del trapezio ad angolo retto.

Come nella figura sopra (b), la superficie piegata Ⅰ-1-Ⅱ-2-Ⅲ-3…XII-12 si estende nella figura mostrata sotto, quindi nella figura sopra la linea di piega Ⅰ-Ⅱ-Ⅲ…XII, ovvero le lunghezze reali Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII e così via lungo la linea. Questo metodo per trovare le lunghezze reali è il metodo del trapezio ad angolo retto.

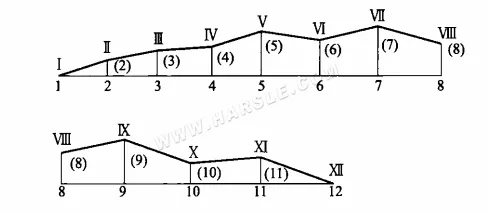
Come si può vedere dal metodo di diagrammazione, anche il metodo del trapezio rettangolo si basa sulla proiezione di una retta inclinata come base, con la distanza dei due punti estremi della retta inclinata dallo stesso piano di proiezione dei due lati retti, dopo aver formato un trapezio rettangolo, quindi l'ipotenusa del trapezio rettangolo, ovvero la lunghezza reale della retta richiesta. Il triangolo rettangolo può essere visto come un caso speciale del metodo del trapezio rettangolo in cui la lunghezza del lato rettangolo è uguale a zero.

Il metodo sopra descritto viene utilizzato per ottenere le due linee laterali di ciascun triangolo sulla superficie del giunto di deformazione a ferro di cavallo, il cui altro lato è la lunghezza dell'apertura circolare superiore e inferiore pari all'arco dispiegato. In questo modo, è possibile ottenere una serie di triangoli con il metodo dei triangoli con tre lati noti, che vengono disposti in modo da ottenere il seguente diagramma del giunto di deformazione a ferro di cavallo.

Metodo di cambio volto

Oltre ai metodi sopra descritti per trovare la lunghezza reale della linea, esiste anche il metodo comune di modificarne la superficie.

Il principio del metodo di modifica della superficie per la lunghezza reale e il metodo di disegno: il principio del metodo di modifica della superficie è quello di mantenere invariato il segmento di spazio, un'altra nuova superficie di proiezione per renderlo parallelo al segmento richiesto e perpendicolare a quello originale, la proiezione del segmento sulla nuova superficie di proiezione rifletterà la sua vera lunghezza. Il diagramma sopra mostra uno schema della lunghezza reale di un segmento di linea.

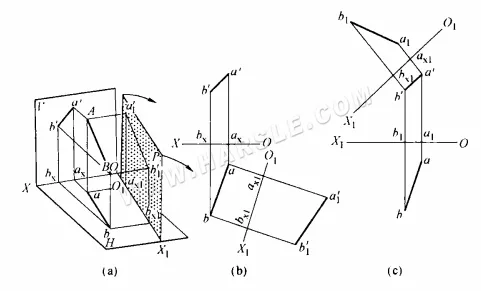
Come si può vedere dal diagramma sopra (a), il segmento AB non è parallelo ai piani di proiezione H e V e la sua proiezione non riflette la lunghezza reale. La nuova proiezione a1'b1′ riflette la lunghezza reale di AB. Un'ulteriore analisi dello spazio mostrato nella figura (a) sopra rivela le seguenti relazioni di proiezione per il metodo della variazione di superficie.

1. Poiché la nuova superficie di proiezione P è parallela ad AB e perpendicolare al piano H, la linea di intersezione tra la nuova superficie di proiezione P e il piano H, O1X1 (chiamata nuovo asse di proiezione), è necessariamente parallela alla proiezione ab del piano H della linea AB, O1X1 // ab, come riflesso nella proiezione del piano H.

2. Poiché le superfici P e V sono simultaneamente perpendicolari alla superficie H, la distanza dalla proiezione a1'b1′ della superficie P a O1X1 e la distanza dalla proiezione a'b' della superficie V a OX devono riflettere simultaneamente le distanze perpendicolari dai due estremi A e B della linea spaziale alla superficie H, e sono uguali tra loro, a1ax1 = a'ax = Aa e b1'bx1 = Bb. Per facilità di designazione, la proiezione appena creata parallela ad AB. La proiezione a1'b1′ che riflette la lunghezza reale è chiamata nuova proiezione, la proiezione a'b' che originariamente non rifletteva la lunghezza reale è chiamata proiezione vecchia o di sostituzione, e la proiezione del piano H che è perpendicolare ad esse allo stesso tempo è chiamata proiezione invariante. In questo modo, questa relazione di proiezione per il metodo della superficie di sostituzione può essere espressa come la distanza dalla nuova proiezione al nuovo asse uguale alla distanza dalla vecchia proiezione al vecchio asse.

3. Poiché entrambe le superfici P e V sono perpendicolari alla superficie H, la connessione tra la proiezione P e la proiezione H in qualsiasi punto della linea deve essere perpendicolare al nuovo asse di proiezione O1X1, la linea tra la proiezione invariante e le proiezioni vecchia e nuova è perpendicolare rispettivamente ai vecchi e nuovi assi di proiezione, dopo lo sviluppo.

In conformità con la relazione di proiezione di cui sopra del metodo di permutazione, i passaggi di creazione del grafico dovrebbero essere

1. come mostrato in (b) sopra, rendere il nuovo asse di proiezione O1X1 parallelo ad ab.

2. Traccia una linea perpendicolare attraverso i punti a e b all'asse O1X1 e interseca O1X1 nei punti ax1 e bx1.

3. Spostare le proiezioni a' e b' del piano V sull'asse OX sul nuovo piano di proiezione, misurare ax1a1'=axa' e bx1b1'=bxb' sulle linee verticali.

4. Collega i punti a1′ e b1′, la nuova proiezione a1'b1′ della linea AB, che riflette la lunghezza reale di AB.

Esempio: il diagramma seguente mostra l'uso del metodo del piano di proiezione ausiliario per trovare la forma reale di una sezione cilindrica.

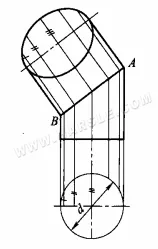
I passaggi del disegno sono i seguenti.

1. creare una vista principale e una vista dall'alto, dividendo la vista dall'alto per 1/2 della circonferenza del cerchio in 6 parti uguali.

2. tracciare una linea verticale verso l'alto attraverso il punto equidistante per indicare la posizione della linea principale nella vista principale.

3. tracciando perpendicolari verso il basso dai punti equidistanti per intersecare la linea centrale inferiore, la larghezza tra le linee semplici della sezione

4. tracciare linee perpendicolari attraverso l'intersezione delle linee sull'apertura obliqua della sezione all'asse lungo parallelo all'apertura obliqua della sezione, e quindi tracciare la distanza tra i punti equidistanti nella vista dall'alto e la linea centrale del cerchio inferiore, a sua volta, ai punti nella vista secondaria, in conformità con la regola della "larghezza uguale".

5. Collegare i punti per creare un'ellisse solida della sezione.

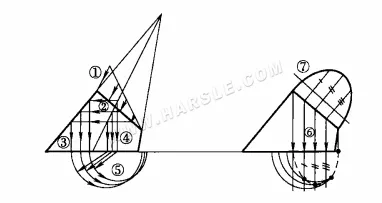
Il diagramma seguente mostra l'uso del metodo del piano di proiezione ausiliario per trovare la forma reale della sezione dell'ortocono. I diagrammi ①, ②, … (7) indicano l'ordine di disegno e le linee di collegamento.

In generale, non è necessario tracciare linee sulla superficie del cono per ottenere la forma reale della sezione conica, ma è meglio utilizzare il metodo del cerchio di trama, come mostrato nella figura sopra. Per rendere più chiare le linee, in questo esempio i tre passaggi del diagramma saranno disegnati separatamente; il diagramma vero e proprio non ha bisogno di essere separato. I passaggi sono i seguenti.

1. Cerchi di trama: la linea di proiezione della sezione è divisa in 6 parti uguali; la linea orizzontale dei punti uguali sopra è intersecata con la linea di contorno; la linea verticale è tracciata verso il basso da ciascun punto di intersezione sulla linea di contorno e intersecata nella parte inferiore del cono; i cerchi di trama sono disegnati a turno con il centro del cerchio O, vedere la figura (a) sopra.

2. Vista dall'alto della sezione trasversale: tracciando una linea verticale che attraversa ciascuna equivocità delle linee della sezione trasversale nella vista principale, intersecando il cerchio di latitudine corrispondente, si ottiene una serie di punti di intersezione; collegando i punti di intersezione, si può ottenere la proiezione della vista dall'alto della sezione trasversale, vedere la figura (b) sopra.

3. Per trovare la forma reale della sezione: tracciare un'ellisse parallela all'asse lungo della sezione 1″7″; tracciare linee perpendicolari da ciascun punto uguale della sezione 1~7 all'asse lungo 1″7″; in conformità con il principio delle larghezze uguali, tracciare una serie di larghezze a, b, c, d ed e della sezione nella vista dall'alto alla proiezione ausiliaria, ottenendo punti 2″, 3″, 4″, 5″ e 6″; collegare i punti, ovvero la forma reale della sezione conica, vedere il diagramma (b) sopra. Figura (c) sopra.

Il diagramma seguente mostra l'uso del metodo della superficie di proiezione ausiliaria per trovare la forma reale della sezione conica obliqua.

L'uso della vista ausiliaria per la forma reale della sezione conica obliqua è simile a quello della forma reale della sezione conica ortogonale. Tuttavia, il cono obliquo ha la caratteristica che la sommità del cono è inclinata da un lato e anche il suo asse è inclinato, in modo che il centro di una serie di cerchi di trama non si trovi nello stesso punto sullo stesso asse. Pertanto, invece di creare cerchi concentrici, si crea un cono con un centro per ogni cerchio di trama. Questa caratteristica può essere padroneggiata seguendo i tre passaggi descritti sopra per disegnare la vista ausiliaria di una sezione solida.

I passaggi specifici del disegno sono i seguenti.

1. Per il cerchio di trama: la linea di sezione 4 parti uguali; per punti uguali della linea orizzontale, intersecante la linea di contorno; dalla linea di contorno sui punti fino alla linea verticale, intersecante il cerchio inferiore; punti uguali della linea orizzontale e l'intersezione dell'asse dei punti per il cerchio di trama del centro, il centro del cerchio al cerchio inferiore; rispettivamente, il centro del cerchio di trama e il raggio corrispondente per il cerchio di trama.

2. La vista dall'alto della sezione: attraverso la vista principale delle linee di sezione di ogni equivoco, le linee verticali di discesa e l'intersezione del cerchio di latitudine corrispondente, che danno luogo a una serie di punti di intersezione; insieme ai punti di intersezione, è possibile ottenere la vista dall'alto della proiezione della sezione.

3. Per creare la forma reale della sezione: in base alla larghezza della forma della sezione trovata nella vista dall'alto, creare una vista ausiliaria di 1/2 per disegnare la forma reale di 1/2 della sezione conica obliqua.

Confronto dei metodi di lunghezza reale

Sulla base dell'analisi di cui sopra, è possibile effettuare un semplice confronto tra i quattro metodi per trovare la lunghezza reale di una linea reale.

Il metodo di rotazione risolve la lunghezza reale modificando la posizione della figura nello spazio, senza modificare la posizione del piano di proiezione.

Il metodo di permutazione risolve la lunghezza reale modificando la posizione del piano di proiezione senza modificare la posizione della figura.

Il metodo del triangolo rettangolo e il metodo del trapezio rettangolo (il metodo del triangolo rettangolo può essere visto come un caso speciale del metodo del trapezio rettangolo) risolvono la linea di lunghezza reale senza modificare né la posizione della figura spaziale né la posizione del piano di proiezione.