Podczas pracy nad projektami kluczowe jest zrozumienie, jak ważne jest określenie rzeczywistej długości elementu. Dokładne pomiary gwarantują idealne dopasowanie elementów i ich prawidłowe działanie. W tym artykule podzielę się praktycznymi metodami i wskazówkami, które okazały się skuteczne w określaniu rzeczywistej długości różnych elementów. Niezależnie od tego, czy zajmujesz się produkcją, czy projektami DIY, opanowanie tej umiejętności może znacznie zwiększyć Twoją precyzję i wydajność. Przyjrzyjmy się najlepszym praktykom w zakresie uzyskiwania dokładnych pomiarów!

W przetwarzaniu blacha Części, często spotykane są przedmioty o różnych kształtach, takie jak rury wentylacyjne, odkształcone połączenia itp. Aby zakończyć ich obróbkę, blacha musi zostać najpierw rozłożona, powierzchnia przedmiotu jest rozkładana na płaszczyźnie zgodnie z jego rzeczywistym kształtem i rozmiarem. Rozkładanie blachy jest procesem przygotowawczym do blacha Materiał, a także warunek konieczny prawidłowej obróbki elementów z blachy. Aby poprawnie narysować schemat rozkładania blachy, konieczna jest znajomość rzeczywistych wymiarów schematu rozkładania lub rzeczywistych wymiarów odpowiednich elementów schematu rozkładania. Gdy trójwymiarowa powierzchnia linii i powierzchnia rzutowania nie są równoległe, rysunki konstrukcyjne w rzucie nie odzwierciedlają jego rzeczywistej długości, dlatego przed rozwinięciem należy zastosować metodę graficzną, aby określić rzeczywistą długość odcinka linii.

Metody wyznaczania rzeczywistej długości odcinka obejmują metodę obrotu, metodę trójkąta prostokątnego, metodę trapezu prostokątnego oraz metodę rzutowania pomocniczego. Znajomość i stosowanie tych metod wyznaczania rzeczywistej długości odcinka jest warunkiem wstępnym i podstawą nabycia umiejętności rozkładania blach.

Metoda rotacji

Metoda obrotu polega na obróceniu pochylonej linii wokół osi prostopadłej do płaszczyzny rzutowania do położenia równoległego do innej płaszczyzny rzutowania, gdzie rzutowany odcinek linii na tej płaszczyźnie rzutowania jest rzeczywistą długością pochylonej linii. Dla wygody graficznej oś zazwyczaj przechodzi nad jednym z punktów końcowych pochyłej linii, punkt końcowy jest środkiem okręgu, a pochyła linia jest promieniem obrotu.

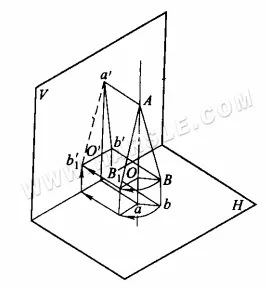
Zasada obrotu dla długości rzeczywistej: poniższy diagram przedstawia zasadę obrotu dla długości rzeczywistej. AB to prosta pozycyjna, nachylona do dowolnej płaszczyzny rzutowania. Rzut AB a'b' na płaszczyznę V i rzut AB na płaszczyznę H są krótsze od długości rzeczywistej. Zakładając, że oś AO jest prostopadła do płaszczyzny H na jednym końcu AB, po obrocie AB wokół osi AO do położenia AB1 równoległego do płaszczyzny V, jego rzut a'b1′ na płaszczyznę V (linia przerywana na diagramie wskazuje długość rzeczywistą) będzie odzwierciedlał jego długość rzeczywistą.

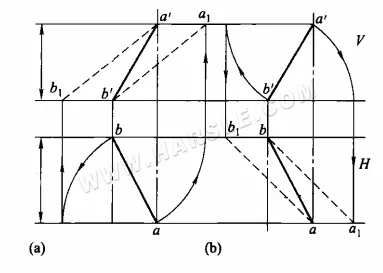
Metoda obrotu dla długości rzeczywistych: Poniższy schemat przedstawia konkretną metodę zastosowania metody obrotu dla długości rzeczywistych. Na poniższym schemacie (a) rzut poziomy ab jest obracany tak, aby był równoległy do rzutu prostokątnego, co skutkuje punktami a1 i b1, łączącymi a1b' lub a'b1, co stanowi rzeczywistą długość odcinka AB; na poniższym schemacie (b) rzut prostokątny a'b' jest obracany tak, aby był równoległy do rzutu poziomego, co skutkuje punktami a1 i b1, łączącymi a1b lub ab1, co stanowi rzeczywistą długość odcinka AB.

Przykład: Poniższy diagram przedstawia rzeczywistą długość graniastosłupa prostego za pomocą metody obrotu. Jak widać z rzutu, podstawa graniastosłupa prostego jest równoległa do płaszczyzny poziomej, a jego rzut poziomy odzwierciedla jego bryłę i rzeczywistą długość. Pozostałe cztery ściany (boki) to dwa zestawy trójkątów, których rzuty nie odzwierciedlają rzeczywistego kształtu. Aby uzyskać rzeczywisty kształt dwóch zestawów trójkątów, należy znaleźć rzeczywistą długość ich graniastosłupów. Ponieważ kształt jest symetryczny od przodu do tyłu, do narysowania diagramu potrzebne są tylko rzeczywiste długości dwóch bocznych graniastosłupów.

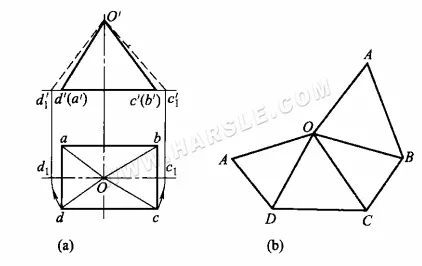
Konkretne kroki tworzenia diagramu rozkładanego to:

1. Użyj metody obrotu, aby znaleźć rzeczywistą długość żeber bocznych Oc i Od. Jak pokazano na poniższym schemacie, przyjmij O jako środek okręgu, odpowiednio Oc, Od jako promień obrotu, przecinając linię poziomą w c1, d1. c1, d1 od c1, d1 w górę linii pionowej, a rzut prostopadły c'd', linia przedłużenia c'd' przecinająca c1'd1', łącząca O'c1', O'd1', to rzeczywista długość graniastosłupa bocznego Oc i Od.

2. Narysuj linię AD o długości równej ad w odpowiednim miejscu na diagramie, a następnie narysuj △AOD, gdzie A i D to środki okręgu, a Od' to promień łuku, przecinający się w punkcie O; następnie narysuj łuk, którego O to środek okręgu, a Oc1′ to promień, przecinający się z łukiem utworzonym z D jako środkiem i dc jako promieniem w punkcie C. Połącz OC i DC, aby uzyskać △DOC. Narysuj pozostałe dwa boki △COB i △BOA w ten sam sposób, aby uzyskać stożek trygonalny z rozszerzonymi bokami.

Poniższy rysunek przedstawia ścięty stożek. Aby najpierw narysować górę stożka, należy przekształcić go w stożek, a następnie utworzyć szereg powierzchni stożka. Następnie należy użyć metody obrotu, aby znaleźć te linie. Część rzeczywistej długości linii została ucięta (można również pozostawić część rzeczywistej długości linii). Można dokonać rozszerzenia rysunku.

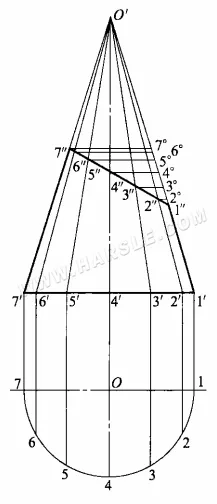
Aby poznać rzeczywistą długość skróconej części linii, należy wykonać następujące kroki diagramu.

1. Przedłuż linię kształtu o 1'1″ i 7'7″ tak, aby się przecięła, tworząc wierzchołek stożka O'.

2. Utwórz okrąg podstawy stożka i podziel obwód okręgu podstawy na liczbę równych części (tutaj 1/2 obwodu okręgu podstawy jest podzielona na 6 równych części), aby uzyskać równe części 1, 2, …, 7, z każdego równego punktu do głównego widoku pionowego prowadzenia, a okrąg podstawy rzutowany jest w punktach 1′, 2′, …, 7′, a następnie z każdego punktu i wierzchołka stożka O' dla linii, aby uzyskać stożek linie powierzchni stożkowej.

3. Spośród linii stożka tylko linie konturowe 1″1′ i 7″7′ są równoległe do rzutu prostopadłego i odzwierciedlają jego długość, podczas gdy pozostałe nie odzwierciedlają długości rzeczywistej. Metoda polega na narysowaniu linii równoległej o długości 7″ z 7″, 6″…, 2″ i przecięciu linii konturowej O'1′ pod kątem 7°, 6°,…, 2°, O'6°, O'5°,…, O'2° dla odpowiednio O'6″, O'5″,…, O'2″. 2″ długości rzeczywistej.

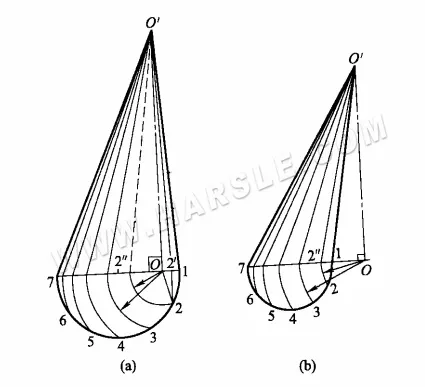
Powyższy diagram przedstawia rzeczywistą długość stożka skośnego po obrocie. Kroki są następujące:

1. Najpierw zrób 1/2 okręgu podstawowego, obwód okręgu podstawowego podziel na pewną liczbę równych części (na schemacie na 6 równych części).

2. z pionową stopą O jako środkiem okręgu, O1, O2, …, O6 dla promienia łuku i 1 ~ 7 przecięciem linii w 2 "i tak w każdym punkcie.

3. Poprowadź linię od punktów 2″ itd. do O', gdzie O'2′ itd. to rzeczywista długość linii przechodzącej przez punkty równonocy. Innymi słowy, O'2′ to rzut prostopadły linii O2, a O'2″ to rzeczywista długość linii O2.

Poniższy diagram przedstawia rzeczywiste długości pryzmatów w połączeniu kwadratowym, uzyskane metodą obrotu i rozciągnięcia.

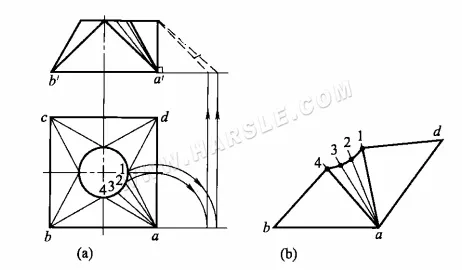
Oto kroki rysowania rzeczywistych długości pryzmatów:

1. Narysuj widok główny i widok z góry, przyrównaj otwór koła widoku z góry i połącz odpowiadające sobie linie proste.

2. Obróć proste linie a1, (a4), a2, (a3) i narysuj pionowe linie w górę, aby wyznaczyć ich rzeczywiste długości a-1, (a-4) i a-2, (a-3) po prawej stronie widoku głównego.

3. Używając rzeczywistych długości prostych linii, długości krawędzi kwadratowych ust i długości rozwarcia łuku odpowiadającego rozwarciu okrągłemu, narysuj po kolei rozwarcia 1/4.

W przypadku, gdy część przejściowa rury kwadratowej znajduje się naprzeciwko rury okrągłej, konieczne jest połączenie kwadratowo-okrągłe. Kwadratowe wejście może być kwadratowe lub prostokątne, a okrągłe może znajdować się pośrodku, z boku lub w narożniku. W związku z tym kształt takich połączeń może być różny, ale metoda wyznaczania rzeczywistej długości połączeń kwadratowych i okrągłych jest zasadniczo taka sama.

Metoda trójkąta prostokątnego

Metoda trójkąta prostokątnego jest powszechnie stosowaną metodą znajdowania długości rzeczywistej.

Zasada metody trójkąta prostokątnego i metoda rysowania: poniższy diagram (a) jest diagramem zasadniczym metody trójkąta prostokątnego dla rzeczywistej długości. Odcinek AB nie jest równoległy do płaszczyzny rzutowania, a jego rzut ab i a'b' nie odzwierciedlają rzeczywistej długości. Na płaszczyźnie ABba poprowadzono prostą równoległą do ab przechodzącą przez punkt A i przecinającą Bb w punkcie B1, dając trójkąt prostokątny ABB1. W tym trójkącie rzeczywistą długość przeciwprostokątnej AB trójkąta prostokątnego można znaleźć, znając długości dwóch boków prostokątnych AB1 i BB1. Długości AB1 i BB1 znajdują się na diagramie rzutowania jako AB1 = ab, BB1 = b'b1′ lub BB1 = b'bx – a'ax. Znajomość takich dwóch boków prostokątnych jednoznacznie rysuje poszukiwany trójkąt prostokątny.

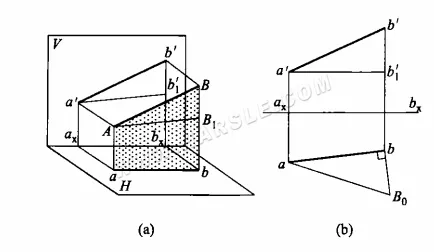
Rysunek (b) powyżej przedstawia zastosowanie metody trójkąta prostokątnego do znalezienia rzeczywistej długości. Rzut odcinka AB jest znany jako ab i a'b'. Aby znaleźć rzeczywistą długość odcinka AB, można najpierw poprowadzić linię poziomą przez punkt a', przeciąć linię bb' w punkcie b1′, bb1′, czyli długość boku prostokątnego. Następnie, patrząc z góry na odcinek AB, narysować linię pionową i przeciąć ją przez punkt b, a następnie linię przecięcia z aB0, czyli rzeczywistą długość odcinka.

Przykład: Poniższy schemat przedstawia małe i duże złącze kwadratowe. Spróbuj znaleźć rzeczywistą długość jego linii głównej AC i linii pomocniczej BC.

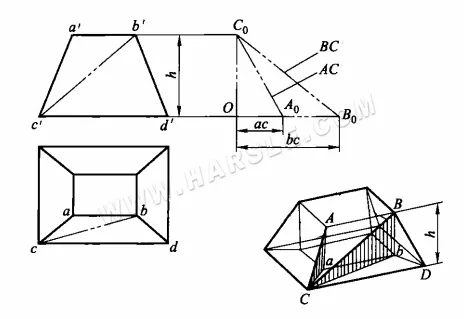
Z diagramu wynika, że rzeczywistą długość AC można znaleźć w trójkącie prostokątnym, gdzie aC i Aa są dwoma bokami prostokątnymi, natomiast rzeczywistą długość BC można znaleźć w trójkącie prostokątnym BbC. W obu trójkątach Aa = Bb = h, co jest równe wysokości stawu. Pozostałe dwa boki prostokątne aC i bC są równe rzutom ac i bc odpowiednio na AC i BC w widoku z góry. W ten sposób rzeczywiste długości AC i BC można wyznaczyć w następujący sposób.

1. utwórz kąt prosty B0OC0.

2. przeciąć OA0 i OB0 na poziomej stronie tego kąta prostego, odpowiednio równe ac i bc w widoku z góry, a także przeciąć OC0 na pionowej stronie, równej wysokości h w widoku głównym.

3. połącz C0A0 i C0B0, wówczas przeciwprostokątne C0A0 i C0B0 będą rzeczywistymi długościami żądanych odcinków AC i BC.

Metoda trapezu prostokątnego

Metoda trapezów prostokątnych jest również powszechnie stosowaną metodą wyznaczania długości rzeczywistych.

Zasada metody trapezów prostokątnych dla długości rzeczywistej i metoda rysowania: poniższy diagram przedstawia zasadę stosowania metody trapezów prostokątnych dla długości rzeczywistej. Ogólne położenie linii AB na powierzchni V i powierzchni H nie może odzwierciedlać długości rzeczywistej, ale dwa punkty końcowe linii AB i odległość między powierzchniami V można uzyskać na powierzchni H, czyli Aa i Bb, te same, A, B dwa punkty i odległość między powierzchniami H można również uzyskać na powierzchni V, czyli Aa' i Bb'. W oparciu o tę zasadę, rzeczywistą długość linii AB można znaleźć za pomocą metody trapezów prostokątnych. Istnieją dwie konkretne metody wykresu długości rzeczywistych.

1. korzystając z rzutu prostokątnego rzeczywistej długości odcinka AB: rzut prostokątny odcinka AB a'b' jako dolnej krawędzi trapezu prostokątnego, z dwóch punktów a', b' odpowiednio w górę odcinka pionowego, przecinają się odcinki Aa', Bb', połączone z odcinkiem AB, tj. dla żądanego odcinka.

2. jest wykorzystaniem rzutu poziomego rzeczywistej długości odcinka AB: rzut poziomy AB jako dolna krawędź trapezu prostokątnego, z dwóch punktów a, b odpowiednio w górę linii pionowej, przecinają się odcinki Aa, Bb, łączą AB, który jest żądany.

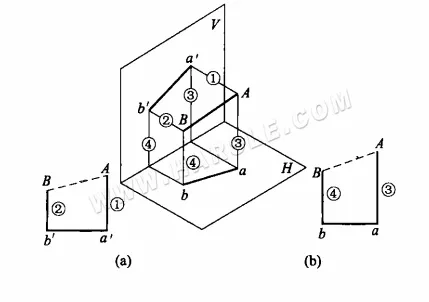
Przykład: Poniższy rysunek przedstawia staw podkowy, którego górny i dolny wylot to okręgi, ale okręgi te nie są równoległe i nie mają równej średnicy. Spróbuj narysować trapez prostokątny na podstawie jego długości linii i diagramu rozszerzenia.

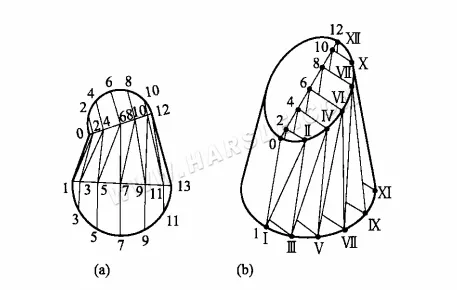
Z powyższego rysunku (a) wynika, że ponieważ jego powierzchnia nie jest powierzchnią stożkową, aby stworzyć diagram jego rozwinięcia, można jedynie wykorzystać linię do i z powierzchni na kilka trójkątów, a następnie, po kolei, znaleźć rzeczywisty kształt tych trójkątów. Szczegółowe kroki wykresu są następujące.

1. Zrób 12 równych części górnego i dolnego otworu ustnego, a następnie podziel powierzchnię na 24 trójkąty, jak pokazano na schemacie.

2. Znajdź rzeczywiste długości linii Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII, a następnie narysuj rzeczywisty kształt serii trójkątów.

W takich przypadkach, jeśli do znalezienia rzeczywistej długości użyta zostanie metoda obrotu lub metoda trójkąta prostokątnego, konieczne będzie wykonanie rzutu odcinka na widok z góry. Ponieważ górna powierzchnia połączenia podkowa i pozioma płaszczyzna rzutowania są nachylone, a zatem górna powierzchnia w widoku z góry jest odbita jako elipsa, te dwie metody rozszerzania mapy są oczywiście bardziej problematyczne. W tym przypadku właściwe jest zastosowanie metody trapezów prostokątnych.

Tak jak na powyższym rysunku (b) w rozciągnięciu powierzchni złożonej Ⅰ-1-Ⅱ-2-Ⅲ-3…XII-12, rozciągniętym na rysunku poniżej, a następnie na rysunku powyżej linii zagięcia Ⅰ-Ⅱ-Ⅲ…XII, czyli o rzeczywistej długości Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII itd. Ta metoda znajdowania rzeczywistych długości to metoda trapezów prostokątnych.

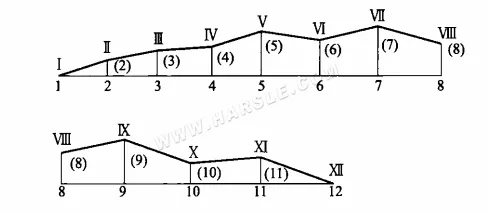
Jak widać z metody diagramowej, metoda trapezu prostokątnego również opiera się na rzucie pochyłej jako podstawy, gdzie odległość dwóch punktów końcowych pochyłej od tej samej płaszczyzny rzutu, co dwa przyprostokątne, po utworzeniu trapezu prostokątnego, wynosi przeciwprostokątną trapezu prostokątnego, czyli rzeczywistą długość poszukiwanej linii. Trójkąt prostokątny można postrzegać jako szczególny przypadek metody trapezu prostokątnego, w którym długość przyprostokątnej jest równa zeru.

Powyższa metoda służy do uzyskania dwóch linii bocznych każdego trójkąta na powierzchni połączenia podkowatego, którego drugi bok jest długością górnego i dolnego otworu kołowego równą rozłożonemu łukowi. W ten sposób można utworzyć serię trójkątów metodą trójkątów o trzech znanych bokach, które są ułożone w celu uzyskania poniższego schematu połączenia podkowatego.

Metoda zmiany twarzy

Oprócz opisanych powyżej metod znajdowania rzeczywistej długości linii, istnieje również powszechnie stosowana metoda polegająca na zmianie powierzchni.

Zasada metody zmiany powierzchni na rzeczywistą długość i metoda rysowania: zasada metody zmiany powierzchni polega na zachowaniu niezmienionego odcinka przestrzeni, a następnie na stworzeniu nowej powierzchni rzutowania, równoległej do żądanego odcinka i prostopadłej do pierwotnej. Rzut odcinka na nową powierzchnię rzutowania będzie odzwierciedlał jego rzeczywistą długość. Powyższy diagram przedstawia schematyczny rysunek rzeczywistej długości odcinka.

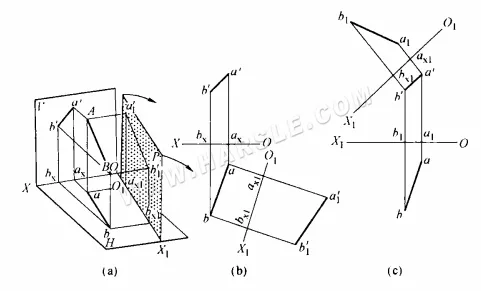
Jak widać na powyższym diagramie (a), odcinek AB nie jest równoległy do płaszczyzn rzutowania H i V, a jego rzut nie odzwierciedla rzeczywistej długości. Nowy rzut a1'b1′ odzwierciedla rzeczywistą długość odcinka AB. Dalsza analiza przestrzeni pokazanej na rysunku (a) powyżej ujawnia następujące zależności rzutowania dla metody zmiany powierzchni.

1. Ponieważ nowa powierzchnia projekcji P jest równoległa do AB i prostopadła do płaszczyzny H, linia przecięcia pomiędzy nową powierzchnią projekcji P i płaszczyzną H, O1X1 (zwana nową osią projekcji) jest koniecznie równoległa do rzutu ab na płaszczyznę H linii AB, O1X1 // ab, jak odbito w rzucie na płaszczyznę H.

2. Ponieważ powierzchnie P i V są jednocześnie prostopadłe do powierzchni H, odległość od rzutu a1'b1′ powierzchni P do O1X1 i odległość od rzutu a'b' powierzchni V do OX muszą jednocześnie odzwierciedlać odległości prostopadłe od dwóch punktów końcowych A i B linii przestrzennej do powierzchni H i są one równe sobie, a1ax1 = a'ax = Aa i b1'bx1 = Bb. Dla ułatwienia oznaczenia, nowo utworzony rzut równoległy do AB Rzut a1'b1′, który odzwierciedla rzeczywistą długość, nazywa się nowym rzutem, rzut a'b', który pierwotnie nie odzwierciedlał rzeczywistej długości, nazywa się starym lub zastępczym rzutem, a rzut płaszczyzny H, który jest do nich prostopadły w tym samym czasie, nazywa się rzutem niezmiennym. W ten sposób tę relację projekcji dla metody powierzchni zastępczej można wyrazić jako odległość od nowej projekcji do nowej osi równą odległości od starej projekcji do starej osi.

3. Ponieważ obie powierzchnie P i V są prostopadłe do powierzchni H, połączenie między projekcją P i projekcją H w dowolnym punkcie linii musi być prostopadłe do nowej osi projekcji O1X1, linia między projekcją niezmienną a starą i nową projekcją jest prostopadła odpowiednio do starej i nowej osi projekcji po rozłożeniu.

Zgodnie z powyższą relacją projekcyjną metody permutacyjnej, kroki wykresu powinny być następujące:

1. jak pokazano w punkcie (b) powyżej, zrób nową oś projekcji O1X1 równoległą do ab.

2. Narysuj linię prostopadłą przez punkty a i b do osi O1X1 i przetnij O1X1 w punktach ax1 i bx1.

3. Przesuń rzuty a' i b' płaszczyzny V na oś OX do nowej płaszczyzny rzutowania, zmierz ax1a1'=axa' i bx1b1'=bxb' na liniach pionowych.

4. Połącz punkty a1′ i b1′, nowy rzut a1'b1′ odcinka AB, który odzwierciedla rzeczywistą długość odcinka AB.

Przykład: Poniższy schemat ilustruje zastosowanie metody rzutowania pomocniczego w celu znalezienia rzeczywistego kształtu przekroju walcowego.

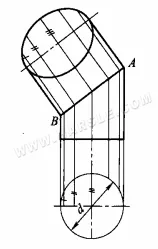
Kroki przedstawione na rysunku są następujące.

1. wykonaj widok główny i widok z góry, dzieląc widok z góry przez połowę obwodu koła na 6 równych części.

2. Narysuj pionową linię biegnącą w górę przez punkt równoodległy, aby określić położenie linii głównej w widoku głównym.

3. rysując prostopadłe w dół od punktów równoodległych, aby przeciąć dolną linię środkową, szerokość między prostymi liniami przekroju

4. rysując linie prostopadłe przechodzące przez przecięcie linii na skośnym otworze przekroju do długiej osi równoległej do skośnego otworu przekroju, a następnie rysując odległość między równoodległymi punktami w widoku górnym a linią środkową dolnego okręgu z kolei do punktów w widoku drugorzędnym, zgodnie z zasadą „równej szerokości”.

5. Połącz punkty tak, aby utworzyć pełną elipsę przekroju.

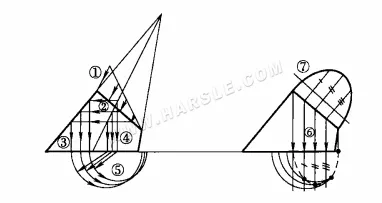
Poniższy schemat przedstawia zastosowanie metody rzutowania pomocniczego do znalezienia rzeczywistego kształtu przekroju stożka ortogonalnego. Schematy ①, ②, … (7) wskazują kolejność rysowania i łączenia linii.

Zasadniczo, nie jest konieczne rysowanie linii na powierzchni stożka, aby uzyskać rzeczywisty kształt przekroju stożkowego, ale lepiej jest zastosować metodę koła wątku, jak pokazano na powyższym rysunku. Aby linie były wyraźne, w tym przykładzie trzy kroki diagramu zostaną narysowane osobno, a sam diagram nie musi być rozdzielony. Kroki są następujące:

1. Koła wątku: linia rzutu przekroju jest podzielona na 6 równych części; linia pozioma powyższych równych punktów jest przecięta linią konturową; linia pionowa jest poprowadzona w dół od każdego punktu przecięcia na linii konturowej i przecina się na dole stożka; koła wątku są kreślone kolejno ze środkiem koła O, patrz rysunek (a) powyżej.

2. Widok przekroju poprzecznego z góry: rysując pionową linię przechodzącą przez każdą równoważność linii przekroju poprzecznego w widoku głównym, przecinającą się z odpowiednim okręgiem szerokości geograficznej, uzyskuje się szereg punktów przecięcia; łącząc punkty przecięcia, można uzyskać rzut przekroju poprzecznego z góry, patrz rysunek (b) powyżej.

3. Aby znaleźć rzeczywisty kształt przekroju: narysuj elipsę równoległą do długiej osi przekroju 1″7″; narysuj linie prostopadłe od każdego równego punktu przekroju 1~7 do długiej osi 1″7″; zgodnie z zasadą równych szerokości narysuj serię szerokości a, b, c, d i e przekroju w widoku z góry do rzutu pomocniczego, co da punkty 2″, 3″, 4″, 5″ i 6″; połącz punkty, czyli rzeczywisty kształt przekroju stożkowego, patrz schemat (b) powyżej. Rysunek (c) powyżej.

Poniższy schemat ilustruje zastosowanie metody pomocniczej powierzchni projekcyjnej w celu znalezienia rzeczywistego kształtu przekroju stożkowego.

Użycie widoku pomocniczego dla rzeczywistego kształtu przekroju stożkowego skośnego jest podobne do użycia widoku pomocniczego dla rzeczywistego kształtu przekroju stożkowego ortogonalnego. Jednakże stożek skośny charakteryzuje się tym, że jego wierzchołek jest nachylony w jedną stronę, a jego oś również jest nachylona, tak że środek szeregu okręgów wątku nie leży w tym samym punkcie na tej samej osi. Dlatego zamiast tworzyć okręgi koncentryczne, tworzy się stożek z jednym środkiem dla każdego okręgu wątku. Tę cechę można opanować, wykonując trzy kroki opisane powyżej, aby narysować widok pomocniczy przekroju pełnego.

Szczegółowe kroki rysowania są następujące.

1. Dla koła wątku: linia przekroju 4 równe części; dla równych punktów linii poziomej, przecinającej się z linią konturową; od linii konturowej w punktach w dół do linii pionowej, przecinającej się z dolnym kołem; równe punkty linii poziomej i punkty przecięcia osi koła wątku ze środkiem, środkiem koła do dolnego koła; odpowiednio środek koła wątku i odpowiedni promień koła wątku.

2. Widok przekroju z góry: poprzez główny widok linii przekroju każdej ekwiwokacji, skierowane w dół linie pionowe i odpowiadające im przecięcia okręgów szerokości geograficznej, co skutkuje serią punktów przecięcia; wraz z punktami przecięcia można uzyskać widok z góry rzutu przekroju.

3. Aby uzyskać rzeczywisty kształt przekroju: na podstawie szerokości kształtu przekroju widocznego w widoku z góry utwórz 1/2 widoku pomocniczego, aby narysować 1/2 rzeczywistego kształtu przekroju stożkowego.

Porównanie metod długości rzeczywistej

Na podstawie powyższej analizy można przeprowadzić proste porównanie czterech metod znajdowania rzeczywistej długości rzeczywistej linii.

Metoda obrotu pozwala na obliczenie rzeczywistej długości poprzez zmianę położenia figury w przestrzeni, bez zmiany położenia płaszczyzny rzutowania.

Metoda permutacji pozwala na znalezienie rzeczywistej długości poprzez zmianę położenia płaszczyzny rzutowania bez zmiany położenia figury.

Metoda trójkątów prostokątnych i metoda trapezów prostokątnych (metodę trójkątów prostokątnych można traktować jako szczególny przypadek metody trapezów prostokątnych) pozwalają wyznaczyć rzeczywistą długość linii, nie zmieniając ani położenia figury przestrzennej, ani położenia płaszczyzny rzutowania.