Ao trabalhar em projetos, é crucial entender a importância de encontrar o comprimento real de um componente. Medições precisas garantem que os componentes se encaixem perfeitamente e funcionem conforme o esperado. Neste artigo, compartilharei métodos e dicas práticas que considero eficazes para determinar o comprimento real de vários componentes. Seja em projetos de manufatura ou "faça você mesmo", dominar essa habilidade pode aumentar muito sua precisão e eficiência. Vamos nos aprofundar nas melhores práticas para obter medições precisas!

No processamento de chapa metálica Peças e peças de vários formatos são frequentemente encontradas, como tubos de ventilação, juntas deformadas, etc. Para concluir o processamento, a chapa metálica deve primeiro ser desdobrada, a superfície do objeto é espalhada em um plano de acordo com sua forma e tamanho reais. O desdobramento da chapa metálica é um processo preparatório para a chapa metálica material, e também é um pré-requisito para o processamento correto das peças de chapa metálica. Para desenhar corretamente um diagrama de desdobramento de chapa metálica, é necessário conhecer as dimensões reais do diagrama de desdobramento ou as dimensões reais dos componentes relevantes do diagrama de desdobramento. Quando a superfície tridimensional da linha e a superfície de projeção não são paralelas, o comprimento real do segmento de linha não é refletido nos desenhos de projeto na projeção. Portanto, antes do desdobramento, deve-se utilizar um método gráfico para descobrir o comprimento real do segmento de linha.

Os métodos para encontrar o comprimento real de um segmento de reta incluem o método da rotação, o método do triângulo retângulo, o método do trapézio retângulo e o método do plano de projeção auxiliar. O domínio e a aplicação desses métodos para encontrar o comprimento real de um segmento de reta são pré-requisitos e a base para a aquisição de habilidades de desdobramento de chapas metálicas.

O Método de Rotação

O método de rotação envolve a rotação de uma reta inclinada em torno de um eixo perpendicular a um plano de projeção até uma posição paralela a outro plano de projeção, onde o segmento de reta projetado nesse plano de projeção é o comprimento real da reta inclinada. Para conveniência gráfica, o eixo geralmente passa sobre um dos pontos finais da reta inclinada, sendo o ponto final o centro do círculo e a reta inclinada o raio de rotação.

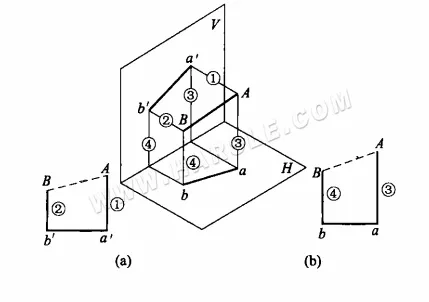
O princípio da rotação para comprimento real: o diagrama abaixo mostra o princípio da rotação para comprimento real. ab é uma reta de posição geral, inclinada em relação a qualquer plano de projeção. A projeção a'b' de ab no plano V e a projeção ab' de ab no plano H são ambas menores que o comprimento real. Supondo que o eixo AO seja perpendicular ao plano H em uma extremidade de AB, quando AB é girado em torno do eixo AO para uma posição AB1 paralela ao plano V, sua projeção a'b1' no plano V (a linha tracejada no diagrama indica o comprimento real) refletirá seu comprimento real.

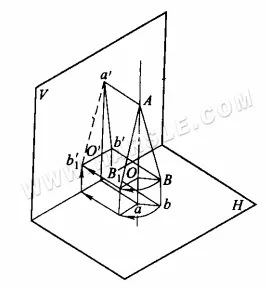
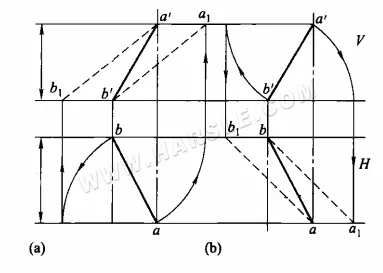
Método de rotação para comprimentos reais: O diagrama abaixo mostra o método específico de utilização do método de rotação para comprimentos reais. No diagrama abaixo (a), a projeção horizontal ab é rotacionada de modo que fique paralela à projeção ortográfica, resultando nos pontos a1 e b1, conectando a1b' ou a'b1, que é o comprimento real do segmento de reta AB; no diagrama abaixo (b), a projeção ortográfica a'b' é rotacionada de modo que fique paralela à projeção horizontal, resultando em a1 e b1, conectando a1b ou ab1, que é o comprimento real do segmento de reta AB.

Exemplo: O diagrama abaixo mostra um diagrama do comprimento real do prisma de um prisma oblíquo usando o método de rotação. Como pode ser visto na projeção, a base do prisma oblíquo é paralela ao plano horizontal e sua projeção horizontal reflete sua forma sólida e comprimento real. As quatro faces restantes (lados) são dois conjuntos de triângulos, cujas projeções não refletem a forma real. Para obter a forma real dos dois conjuntos de triângulos, o comprimento real de seus prismas deve ser encontrado. Como a forma é simétrica da frente para trás, apenas os comprimentos reais dos dois prismas laterais são necessários para desenhar o diagrama.

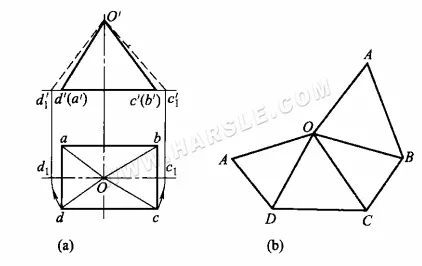
As etapas específicas para fazer um diagrama de desdobramento são

1. Use o método de rotação para encontrar os comprimentos reais das nervuras laterais Oc e Od. Conforme mostrado no diagrama abaixo, tome O como o centro do círculo, respectivamente Oc, Od como o raio de rotação, cruze a linha horizontal em c1, d1. c1, d1 de c1, d1 para cima a linha vertical, e projeção ortográfica c'd' linha de extensão interceptada em c1'd1', conectando O'c1', O'd1' é o comprimento real do prisma lateral Oc e Od.

2. Trace uma reta AD de comprimento igual a ad na posição apropriada no diagrama e, em seguida, desenhe △AOD com A e D como o centro do círculo e Od' como o raio do arco, interseccionando em O; em seguida, trace um arco com O como o centro do círculo e Oc1' como o raio, interseccionando com o arco feito com D como o centro e dc como o raio em C. Conecte OC e DC para obter △DOC. Desenhe os dois lados restantes de △COB e △BOA da mesma forma para obter um cone trigonal com os lados expandidos.

A figura abaixo é um cone truncado, o comprimento real do cone e a expansão, deve primeiro desenhar o topo do cone, tornar-se um cone completo e, em seguida, fazer uma série de superfícies de cone e usar o método de rotação para encontrar essas linhas foram truncadas parte do comprimento real da linha (também disponível para deixar parte do comprimento real da linha), você pode fazer a expansão da figura.

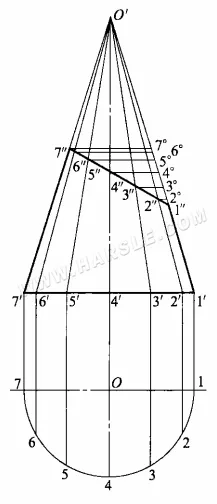
Para encontrar o comprimento real da parte truncada da linha, as etapas do diagrama são as seguintes.

1. Estenda a linha de forma 1'1″ e 7'7″ para interceptá-la, resultando no topo do cone O'.

2. Faça o círculo base do cone e divida a circunferência do círculo base em um número de partes iguais (aqui, 1/2 da circunferência do círculo base é dividida em 6 partes iguais), para obter partes iguais 1, 2, …, 7, de cada ponto igual à vista principal da derivação vertical e a projeção ortogonal do círculo base interceptada em 1′, 2′, …, 7′ pontos e, em seguida, de cada ponto e do topo do cone O' para a linha, para obter o cone as linhas da superfície cônica.

3. Entre as linhas do cone, apenas as linhas de contorno 1″1′ e 7″7′ são paralelas à projeção ortogonal e refletem seu comprimento, enquanto as demais não refletem o comprimento real. O método consiste em traçar uma linha paralela de 7'1′ a partir de 7″, 6″…, 2″ e interceptar a linha de contorno O'1′ em 7°, 6°,…, 2°, O'6°, O'5°,…, O'2° para O'6″, O'5″,…, O' 2″, respectivamente. 2″ de comprimento real.

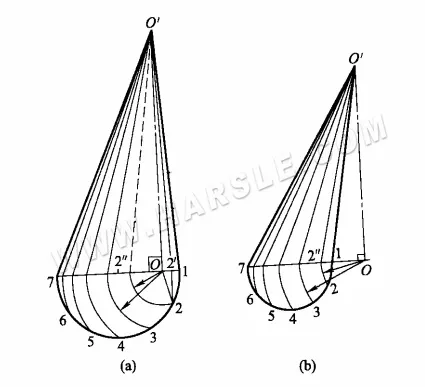
O diagrama acima mostra o comprimento real do cone inclinado por rotação. Os passos são os seguintes.

1. primeiro faça 1/2 do círculo base, a circunferência do círculo base em um número de partes iguais (no diagrama em 6 partes iguais).

2. com o pé vertical O como centro do círculo, O1, O2, …, O6 para o raio do arco e 1 ~ 7 intersecções de linhas em 2 “e assim por diante em cada ponto.

3. Trace uma reta dos pontos 2″ etc. até O', sendo O'2′ etc. o comprimento real da reta que passa pelos equinócios. Em outras palavras, O'2′ é a projeção ortogonal da reta O2 e O'2″ é o comprimento real da reta O2.

O diagrama abaixo mostra os comprimentos reais dos prismas de uma junta quadrada usando o método de rotação e expandindo-os.

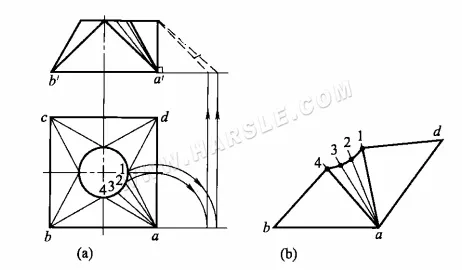
Os passos para desenhar os comprimentos reais dos prismas são

1. desenhe a vista principal e a vista superior, iguale a abertura do círculo da vista superior e conecte as linhas simples correspondentes.

2. gire as linhas simples a1, (a4), a2, (a3) e desenhe linhas verticais para cima para derivar seus comprimentos reais a-1, (a-4) e a-2, (a-3) no lado direito da vista principal.

3. Usando os comprimentos reais da linha simples, os comprimentos da borda da boca quadrada e os comprimentos equivalentes do arco da boca redonda, desenhe as extensões de 1/4 uma de cada vez.

Onde a parte de transição do tubo quadrado é oposta ao tubo redondo, deve haver uma junta quadrada-redonda. A boca quadrada pode ser quadrada ou retangular, a boca redonda pode estar no centro, em um dos lados ou em um dos cantos; portanto, o formato dessas juntas pode variar, mas o método para encontrar o comprimento real das juntas quadrada e redonda é basicamente o mesmo.

Método do Triângulo Retângulo

O método do triângulo retângulo é um método comumente usado para encontrar o comprimento real.

O princípio do método do triângulo retângulo e o método de desenho: o diagrama a seguir (a) é o diagrama principal do método do triângulo retângulo para comprimento real. O segmento de reta AB não é paralelo ao plano de projeção, e suas projeções ab e a'b' não refletem o comprimento real. No plano ABba, uma reta é paralela a ab através do ponto A e intercepta Bb no ponto B1, resultando no triângulo retângulo ABB1. Neste triângulo, o comprimento real da hipotenusa AB do triângulo retângulo pode ser encontrado conhecendo-se os comprimentos dos dois lados retângulos AB1 e BB1. E os comprimentos de AB1 e BB1 são encontrados no diagrama de projeção como AB1 = ab, BB1 = b'b1', ou BB1 = b'bx – a'ax. Conhecer esses dois lados retângulos desenha de forma única o triângulo retângulo procurado.

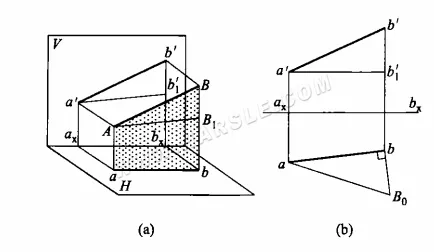
A Figura (b) acima mostra o uso do método do triângulo retângulo para encontrar o comprimento real. A projeção da reta AB é conhecida como ab e a'b'. Para encontrar o comprimento real de AB, você pode primeiro traçar uma reta horizontal passando pelo ponto a', cruzando a reta bb' no ponto b1', bb1', ou seja, o comprimento de um lado reto da solicitação. Em seguida, a vista superior de ab para outra aresta reta, sobre o ponto b, cita a reta vertical e intercepta bB0 = b'b1', conectada a aB0, ou seja, o comprimento real do segmento de reta.

Exemplo: O diagrama abaixo mostra uma junta de boca quadrada pequena e grande. Tente encontrar o comprimento real de sua linha principal AC e linha auxiliar BC.

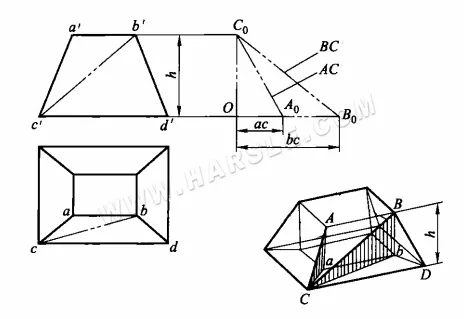
Pode-se observar no diagrama que o comprimento real AC pode ser encontrado em um triângulo retângulo com aC e Aa como dois lados retângulos, enquanto o comprimento real BC pode ser encontrado no triângulo retângulo BbC. Em ambos os triângulos, Aa = Bb = h, que é igual à altura da junta. Os outros dois lados retângulos aC e bC são iguais às projeções ac e bc de AC e BC na vista superior, respectivamente. Dessa forma, os comprimentos reais de AC e BC podem ser encontrados da seguinte forma.

1. faça um ângulo reto B0OC0.

2. intercepte OA0 e OB0 no lado horizontal desse ângulo reto, respectivamente igual a ac e bc na vista superior, e intercepte OC0 no lado vertical igual à altura h na vista principal.

3. conecte C0A0 e C0B0, então as hipotenusas C0A0 e C0B0 são os comprimentos reais dos AC e BC solicitados.

O Método do Trapézio Retângulo

O método do trapézio retângulo também é um método comum para encontrar comprimentos reais.

Princípio do método do trapézio retângulo para comprimento real e método de desenho: o diagrama a seguir mostra o princípio do uso do método do trapézio retângulo para comprimento real. A localização geral da reta AB na superfície V e na superfície H não pode refletir o comprimento real, mas os dois pontos finais da reta AB e a distância entre a superfície V podem ser obtidos na superfície H, ou seja, Aa e Bb, os mesmos dois pontos A, B e a distância entre a superfície H também podem ser obtidos na superfície V, ou seja, Aa e Bb. Com base nesse princípio, o comprimento real da reta AB pode ser encontrado usando o método do trapézio retângulo. Existem dois métodos específicos para representar graficamente os comprimentos reais.

1. usando a projeção ortográfica do comprimento real da linha AB: a projeção ortográfica de AB a'b' como a aresta inferior do trapézio retângulo, de a', b' dois pontos respectivamente acima da linha vertical, intercepte o comprimento de Aa', Bb', conectado a AB, ou seja, para o solicitado.

2. é o uso da projeção horizontal do comprimento real do segmento de reta AB: a projeção horizontal de AB como a aresta inferior de um trapézio retângulo, de a, b dois pontos respectivamente para cima da linha vertical, interceptam o comprimento de Aa, Bb, conectam AB que é o solicitado.

Exemplo: A figura a seguir mostra uma junta de deformação em ferradura, suas bocas superior e inferior são círculos, mas os dois círculos não são paralelos e não são iguais em diâmetro; tente fazer um método trapezoidal de ângulo reto com seu comprimento de linha e diagrama de expansão.

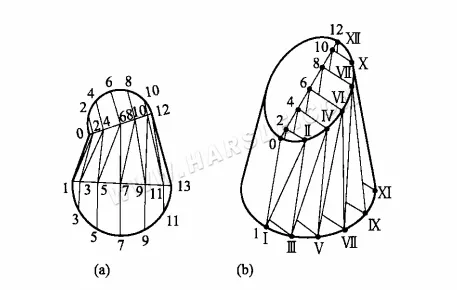
A partir da figura (a) acima, pode-se observar que, como sua superfície não é cônica, para construir seu diagrama de expansão, basta usar a reta que vai e vem da superfície em vários triângulos e, um por um, encontrar a forma real desses triângulos. As etapas específicas da construção gráfica são as seguintes.

1. Faça 12 partes iguais das bocas superior e inferior e divida a superfície em 24 triângulos, conforme mostrado no diagrama.

2. Encontre os comprimentos reais das retas Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII e, em seguida, faça a forma real da série de triângulos.

Para tais exemplos, se o método de rotação ou o método do triângulo retângulo for usado para encontrar o comprimento real, a projeção do segmento de reta na vista superior deve ser feita. Como a superfície superior da junta de deformação em ferradura e o plano de projeção horizontal são inclinados, a superfície superior na vista superior é refletida como uma elipse. Obviamente, esses dois métodos para a expansão do mapa são mais problemáticos. Neste momento, é apropriado usar o método trapezoidal em ângulo reto.

Como na figura acima (b), na superfície dobrada Ⅰ-1-Ⅱ-2-Ⅲ-3…XII-12, estende-se para a figura mostrada abaixo, e então a figura acima da linha de dobra Ⅰ-Ⅱ-Ⅲ…XII, ou seja, o comprimento real Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII e assim por diante. Este método para encontrar os comprimentos reais é o método do trapézio retângulo.

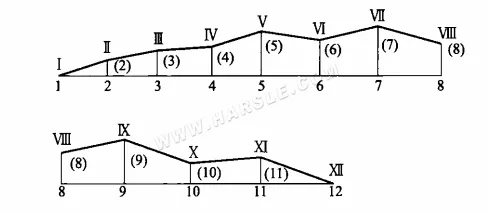
Como pode ser visto no método de diagramação, o método do trapézio retângulo também se baseia na projeção de uma reta inclinada como base, com a distância dos dois pontos extremos da reta inclinada a partir do mesmo plano de projeção que os dois lados retos. Após a formação de um trapézio retângulo, a hipotenusa do trapézio retângulo, ou seja, o comprimento real da reta solicitada, é calculada. O triângulo retângulo pode ser visto como um caso especial do método do trapézio retângulo, em que o comprimento do lado reto é igual a zero.

O método acima é usado para obter as duas linhas laterais de cada triângulo na superfície da junta de deformação em ferradura, cujo outro lado é o comprimento da abertura circular superior e inferior igual ao arco desdobrado. Dessa forma, uma série de triângulos pode ser formada pelo método dos triângulos com três lados conhecidos, que são dispostos de forma a obter o seguinte diagrama da junta de deformação em ferradura.

Método de Mudança de Rosto

Além dos métodos acima para encontrar o comprimento real da linha, há também o método comum de alterar a superfície.

O princípio do método de alteração da superfície para o comprimento real e o método de desenho: o princípio do método de alteração da superfície é manter o segmento espacial inalterado, criando outra nova superfície de projeção para torná-lo paralelo ao segmento solicitado e perpendicular ao original. A projeção do segmento na nova superfície de projeção refletirá seu comprimento real. O diagrama acima mostra um diagrama esquemático do comprimento real de um segmento de reta.

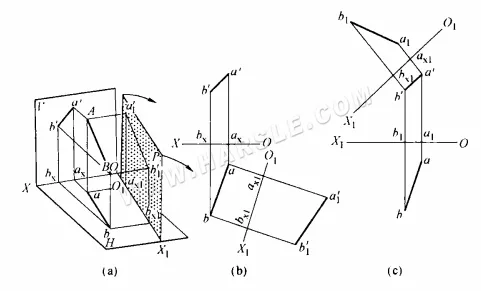
Como pode ser visto no diagrama acima (a), o segmento de reta AB não é paralelo aos planos de projeção H e V e sua projeção não reflete o comprimento real. A nova projeção a1'b1' reflete o comprimento real de AB. Uma análise mais aprofundada do espaço mostrado na figura (a) acima revela as seguintes relações de projeção para o método de mudança de superfície.

1. Como a nova superfície de projeção P é paralela a AB e perpendicular ao plano H, então a linha de intersecção entre a nova superfície de projeção P e o plano H, O1X1 (chamada de novo eixo de projeção), é necessariamente paralela à projeção ab do plano H da linha AB, O1X1 // ab, conforme refletido na projeção do plano H.

2. Como as superfícies P e V são simultaneamente perpendiculares à superfície H, a distância da projeção a1'b1' da superfície P até O1X1 e a distância da projeção a'b' da superfície V até OX devem refletir simultaneamente as distâncias perpendiculares dos dois pontos finais A e B da linha espacial até a superfície H, e são iguais entre si, a1ax1 = a'ax = Aa e b1'bx1 = Bb. Para facilitar a designação, a projeção recém-feita paralela a AB A projeção a1'b1' que reflete o comprimento real é chamada de nova projeção, a projeção a'b' que originalmente não refletia o comprimento real é chamada de projeção antiga ou de substituição, e a projeção do plano H que é perpendicular a elas ao mesmo tempo é chamada de projeção invariante. Dessa forma, essa relação de projeção para o método da superfície de substituição pode ser expressa como a distância da nova projeção ao novo eixo sendo igual à distância da projeção antiga ao eixo antigo.

3. Como as superfícies P e V são perpendiculares à superfície H, a conexão entre a projeção P e a projeção H em qualquer ponto da linha deve ser perpendicular ao novo eixo de projeção O1X1, a linha entre a projeção invariante e as projeções antiga e nova é perpendicular aos eixos de projeção antigo e novo, respectivamente, após o desdobramento.

De acordo com a relação de projeção acima do método de permutação, as etapas de representação gráfica devem ser

1. conforme mostrado em (b) acima, faça o novo eixo de projeção O1X1 paralelo a ab.

2. Desenhe uma linha perpendicular através dos pontos a e b até o eixo O1X1 e intersecte O1X1 nos pontos ax1 e bx1.

3. Mova as projeções a' e b' do plano V para o eixo OX para o novo plano de projeção, meça ax1a1'=axa' e bx1b1'=bxb' nas linhas verticais.

4. Conecte os pontos a1′ e b1′, a nova projeção a1'b1′ da reta AB, que reflete o comprimento real de AB.

Exemplo: O diagrama abaixo mostra o uso do método do plano de projeção auxiliar para encontrar a forma real de uma seção cilíndrica.

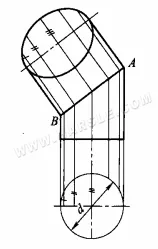
Os passos no desenho são os seguintes.

1. faça uma vista principal e superior, dividindo a vista superior pela metade da circunferência do círculo em 6 partes iguais.

2. desenhe uma linha vertical para cima através do ponto equidistante para fornecer a posição da linha principal na vista principal.

3. traçar perpendiculares para baixo a partir dos pontos equidistantes para interceptar a linha central inferior, a largura entre as linhas planas da seção

4. traçar linhas perpendiculares através da intersecção das linhas na abertura oblíqua da seção até o eixo longo paralelo à abertura oblíqua da seção e, em seguida, traçar a distância entre os pontos equidistantes na vista superior e a linha central do círculo inferior, por sua vez, até os pontos na vista secundária, de acordo com a regra de “largura igual”.

5. Conecte os pontos para criar uma elipse sólida da seção.

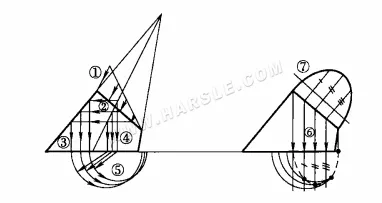
O diagrama abaixo mostra o uso do método do plano de projeção auxiliar para encontrar a forma real da seção ortocone. Os diagramas ①, ②, … (7) indicam a ordem de desenho e conexão das linhas.

Em geral, não é necessário traçar linhas na superfície do cone para criar a forma real da seção cônica, mas é melhor usar o método do círculo de trama, como mostrado na figura acima. Para tornar as linhas mais claras, as três etapas do diagrama serão desenhadas separadamente neste exemplo; o diagrama real não precisa ser separado. As etapas são as seguintes.

1. Círculos de trama: a linha de projeção da seção é dividida em 6 partes iguais; a linha horizontal dos pontos iguais acima é interceptada com a linha de contorno; a linha vertical é desenhada para baixo a partir de cada ponto de intersecção na linha de contorno e interceptada na parte inferior do cone; os círculos de trama são desenhados por sua vez com o centro do círculo O, veja a figura (a) acima.

2. Vista superior da seção transversal: desenhando uma linha vertical através de cada equívoco das linhas da seção transversal na vista principal, cruzando com o círculo de latitude correspondente, obtém-se uma série de pontos de intersecção; conectando os pontos de intersecção, obtém-se a projeção da vista superior da seção transversal, veja a figura (b) acima.

3. Para encontrar a forma real da seção: faça uma elipse paralela ao eixo longo da seção 1″7″; desenhe linhas perpendiculares de cada ponto igual da seção 1~7 até o eixo longo 1″7″; de acordo com o princípio de larguras iguais, desenhe uma série de larguras a, b, c, d e e da seção na vista superior para a projeção auxiliar, resultando em pontos de 2″, 3″, 4″, 5″ e 6″; conecte os pontos, ou seja, a forma real da seção cônica, veja o diagrama (b) acima. Figura (c) acima.

O diagrama abaixo mostra o uso do método da superfície de projeção auxiliar para encontrar a forma real da seção cônica oblíqua.

O uso da vista auxiliar para a forma real da seção cônica oblíqua é semelhante ao da forma real da seção cônica ortogonal. No entanto, o cone oblíquo tem a característica de que o topo do cone é inclinado para um lado e seu eixo também é inclinado, de modo que o centro de uma série de círculos de trama não se encontra no mesmo ponto no mesmo eixo. Portanto, em vez de fazer círculos concêntricos, um cone é feito com um centro para cada círculo de trama. Essa característica pode ser dominada seguindo os três passos descritos acima para desenhar a vista auxiliar de uma seção sólida.

As etapas específicas do desenho são as seguintes.

1. Para o círculo de trama: a linha de seção 4 partes iguais; para pontos iguais da linha horizontal, cruzando com a linha de contorno; da linha de contorno nos pontos até a linha vertical, cruzando com o círculo inferior; pontos iguais da linha horizontal e a intersecção do eixo dos pontos para o círculo de trama do centro, o centro do círculo para o círculo inferior; respectivamente, o centro do círculo de trama e o raio correspondente para o círculo de trama.

2. A vista superior da seção: através da vista principal das linhas de seção de cada equívoco, linhas verticais descendentes e a intersecção do círculo de latitude correspondente, resultando em uma série de pontos de intersecção; junto com os pontos de intersecção, você pode obter a vista superior da projeção da seção.

3. Para fazer a forma real da seção: de acordo com a largura da forma da seção encontrada na vista superior, faça 1/2 vista auxiliar para desenhar a forma real 1/2 da seção cônica oblíqua.

Comparação de métodos de comprimento real

Com base na análise acima, uma comparação simples pode ser feita entre os quatro métodos para encontrar o comprimento real de uma reta real.

O método de rotação resolve o comprimento real alterando a posição da figura no espaço, sem alterar a posição do plano de projeção.

O método de permutação resolve o comprimento real alterando a posição do plano de projeção sem alterar a posição da figura.

O método do triângulo retângulo e o método do trapézio retângulo (o método do triângulo retângulo pode ser visto como um caso especial do método do trapézio retângulo) resolvem a linha de comprimento real sem alterar nem a posição da figura espacial nem a posição do plano de projeção.