Bei der Arbeit an Projekten ist es entscheidend, die tatsächliche Länge eines Bauteils zu kennen. Genaue Messungen stellen sicher, dass die Komponenten perfekt zusammenpassen und wie vorgesehen funktionieren. In diesem Artikel teile ich praktische Methoden und Tipps, die ich zur Bestimmung der tatsächlichen Länge verschiedener Bauteile als effektiv empfunden habe. Ob in der Fertigung oder bei Heimwerkerprojekten – die Beherrschung dieser Fähigkeit kann Ihre Präzision und Effizienz erheblich steigern. Lassen Sie uns die besten Vorgehensweisen für genaue Messungen näher betrachten!

Bei der Verarbeitung von Blech Teile, Werkstücke unterschiedlicher Form sind häufig anzutreffen, wie z. B. Lüftungsrohre, deformierte Verbindungen usw. Um ihre Bearbeitung abzuschließen, muss das Blech zunächst entfaltet werden, die Oberfläche des Objekts wird entsprechend seiner tatsächlichen Form und Größe auf einer Ebene ausgebreitet. Das Entfalten von Blech ist ein vorbereitender Prozess für die Blech Material und ist zudem Voraussetzung für die korrekte Verarbeitung der Blechteile. Um ein Blechabwicklungsdiagramm korrekt zeichnen zu können, ist es notwendig, die tatsächlichen Abmessungen des Abwicklungsdiagramms bzw. die tatsächlichen Abmessungen der relevanten Komponenten des Abwicklungsdiagramms zu kennen. Wenn die dreidimensionale Oberfläche der Linie und die Projektionsfläche nicht parallel sind, wird die tatsächliche Länge der Konstruktionszeichnung in der Projektion nicht wiedergegeben. Daher muss vor der Abwicklung eine grafische Methode verwendet werden, um die tatsächliche Länge des Liniensegments zu ermitteln.

Zu den Methoden zur Berechnung der tatsächlichen Länge eines Liniensegments gehören die Rotationsmethode, die Methode des rechtwinkligen Dreiecks, die Methode des rechtwinkligen Trapezes und die Methode der Hilfsprojektionsebene. Die Beherrschung und Anwendung dieser Methoden zur Ermittlung der tatsächlichen Länge eines Liniensegments ist Voraussetzung und Grundlage für den Erwerb von Fähigkeiten zur Blechabwicklung.

Die Rotationsmethode

Bei der Rotationsmethode wird eine geneigte Linie um eine Achse senkrecht zu einer Projektionsebene in eine Position parallel zu einer anderen Projektionsebene gedreht, wobei das projizierte Liniensegment auf dieser Projektionsebene der tatsächlichen Länge der geneigten Linie entspricht. Zur Vereinfachung der Darstellung verläuft die Achse in der Regel über einen der Endpunkte der geneigten Linie, der Endpunkt ist der Mittelpunkt des Kreises und die geneigte Linie der Radius der Rotation.

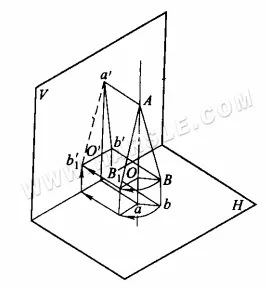
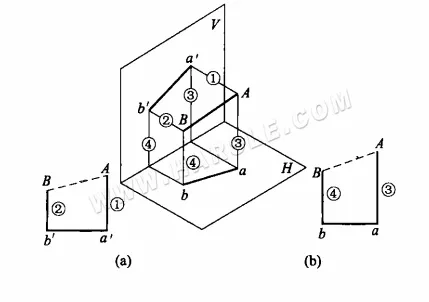
Das Rotationsprinzip für die reale Länge: Das folgende Diagramm zeigt das Rotationsprinzip für die reale Länge. ab ist eine allgemeine Positionslinie, die zu jeder Projektionsebene geneigt ist. Die Projektionen a'b' von ab auf die V-Ebene und ab's Projektion auf die H-Ebene sind beide kürzer als die reale Länge. Unter der Annahme, dass die Achse AO an einem Ende von AB senkrecht zur H-Ebene steht, spiegelt die Projektion a'b1′ von AB auf die V-Ebene (die gestrichelte Linie im Diagramm zeigt die reale Länge an) seine reale Länge wider, wenn AB um die AO-Achse in eine Position AB1 parallel zur V-Ebene gedreht wird.

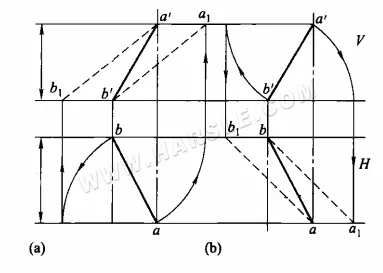
Rotationsmethode für reale Längen: Das folgende Diagramm zeigt die spezifische Methode zur Verwendung der Rotationsmethode für reale Längen. Im folgenden Diagramm (a) wird die horizontale Projektion ab so gedreht, dass sie parallel zur orthographischen Projektion ist, wodurch die Punkte a1 und b1 entstehen, die a1b' oder a'b1 verbinden, was die reale Länge des Liniensegments AB darstellt; im folgenden Diagramm (b) wird die orthographische Projektion a'b' so gedreht, dass sie parallel zur horizontalen Projektion ist, wodurch a1 und b1 entstehen, die a1b oder ab1 verbinden, was die reale Länge des Liniensegments AB darstellt.

Beispiel: Das folgende Diagramm zeigt die tatsächliche Länge eines schiefwinkligen Prismas mithilfe der Rotationsmethode. Wie aus der Projektion ersichtlich ist, verläuft die Basis des schiefwinkligen Prismas parallel zur Horizontalen, und seine horizontale Projektion spiegelt seine räumliche Form und tatsächliche Länge wider. Die verbleibenden vier Flächen (Seiten) sind zwei Dreieckspaare, deren Projektionen nicht die tatsächliche Form widerspiegeln. Um die tatsächliche Form der beiden Dreieckspaare zu ermitteln, muss die tatsächliche Länge ihrer Prismen ermittelt werden. Da die Form von vorne nach hinten symmetrisch ist, werden zum Zeichnen des Diagramms nur die tatsächlichen Längen der beiden seitlichen Prismen benötigt.

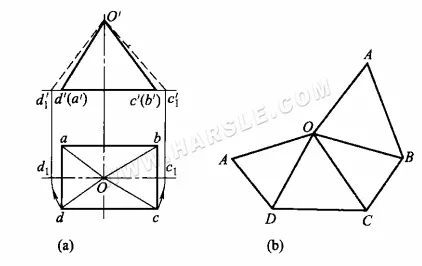
Die einzelnen Schritte zur Erstellung eines Entfaltungsdiagramms sind

1. Verwenden Sie die Rotationsmethode, um die tatsächlichen Längen der seitlichen Rippen Oc und Od zu ermitteln. Wie in der folgenden Abbildung gezeigt, nehmen Sie O als Mittelpunkt des Kreises bzw. Oc, Od als Radius der Rotation, kreuzen Sie die horizontale Linie in c1, d1. c1, d1 von c1, d1 nach oben die vertikale Linie, und die orthographische Projektion c'd' Verlängerungslinie schneidet sich in c1'd1′, verbindet O'c1′, O'd1′ ist die tatsächliche Länge des Seitenprismas Oc und Od.

2. Zeichnen Sie an der entsprechenden Stelle im Diagramm eine Linie AD mit der Länge ad und zeichnen Sie dann △AOD mit A und D als Kreismittelpunkt und Od' als Radius des Bogens, der sich bei O schneidet. Zeichnen Sie dann einen Bogen mit O als Kreismittelpunkt und Oc1' als Radius, der sich mit dem Bogen schneidet, der mit D als Mittelpunkt und dc als Radius bei C gezeichnet wurde. Verbinden Sie OC und DC, um △DOC zu erhalten. Zeichnen Sie die verbleibenden beiden Seiten von △COB und △BOA auf die gleiche Weise, um einen dreieckigen Kegel mit erweiterten Seiten zu erhalten.

Die folgende Abbildung zeigt einen Kegelstumpf mit der tatsächlichen Länge und Ausdehnung des Kegels. Zeichnen Sie zunächst die Spitze des Kegels, um einen vollständigen Kegel zu erhalten. Erstellen Sie dann eine Reihe von Kegeloberflächen. Verwenden Sie die Rotationsmethode, um herauszufinden, welche Linien abgeschnitten wurden und welche Teile der tatsächlichen Länge der Linien übrig bleiben. Sie können dann die Ausdehnung der Abbildung vornehmen.

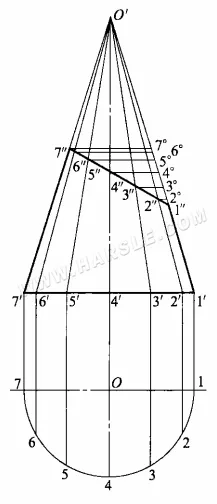
Um die tatsächliche Länge des abgeschnittenen Teils der Linie zu ermitteln, sind die Diagrammschritte wie folgt.

1. Verlängern Sie die Formlinien 1'1″ und 7'7″ bis zum Schnittpunkt, wodurch die Spitze des Kegels O‘ entsteht.

2. Zeichnen Sie den Grundkreis des Kegels und teilen Sie den Umfang des Grundkreises in mehrere gleiche Teile (hier wird 1/2 des Umfangs des Grundkreises in 6 gleiche Teile geteilt), um die gleichen Teile 1, 2, …, 7 zu erhalten, von jedem gleichen Punkt zur Hauptansicht der vertikalen Linie und der orthogonalen Projektion des Grundkreises, die sich an den Punkten 1′, 2′, …, 7′ schneidet, und dann von jedem Punkt zur Spitze des Kegels O‘ für die Linie, um die Linien der Kegeloberfläche des Kegels zu erhalten.

3. Von den Linien des Kegels sind nur die Umrisslinien 1″1′ und 7″7′ parallel zur orthogonalen Projektion und spiegeln deren Länge wider, während der Rest nicht die tatsächliche Länge widerspiegelt. Die Methode besteht darin, aus 7″, 6″…, 2″ eine parallele Linie von 7'1′ zu erstellen und die Konturlinie O'1′ bei 7°, 6°,…, 2°, O'6°, O'5°,…, O'2° für O'6″, O'5″,…, O' 2″ zu schneiden. 2″ tatsächliche Länge.

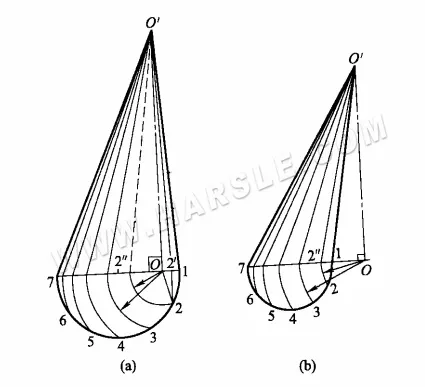
Das obige Diagramm zeigt die tatsächliche Länge des schiefen Kegels durch Rotation. Die Schritte sind wie folgt.

1. Zuerst den Grundkreis zur Hälfte teilen, den Umfang des Grundkreises in mehrere gleich große Teile (im Diagramm in 6 gleich große Teile).

2. mit dem vertikalen Fuß O als Mittelpunkt des Kreises, O1, O2, …, O6 für den Radius des Bogens und 1 ~ 7 Linienschnittpunkt bei 2“ und so weiter für jeden Punkt.

3. Zeichnen Sie eine Linie von den Punkten 2″ usw. nach O‘, O‘2′ usw., wobei die tatsächliche Länge der Linie durch die Tagundnachtgleichen gilt. Mit anderen Worten: O‘2′ ist die orthogonale Projektion der Linie O2 und O‘2″ ist die tatsächliche Länge der Linie O2.

Das folgende Diagramm zeigt die tatsächlichen Längen der Prismen einer Vierkantverbindung unter Verwendung der Rotationsmethode und deren Ausdehnung.

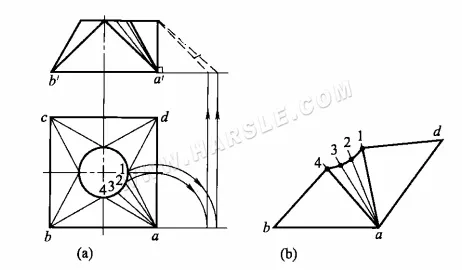
Die Schritte zum Zeichnen der tatsächlichen Längen der Prismen sind

1. Zeichnen Sie die Hauptansicht und die Draufsicht, gleichen Sie die Kreisöffnung der Draufsicht an und verbinden Sie die entsprechenden einfachen Linien.

2. Drehen Sie die einfachen Linien a1, (a4), a2, (a3) und zeichnen Sie vertikale Linien nach oben, um ihre tatsächlichen Längen a-1, (a-4) und a-2, (a-3) auf der rechten Seite der Hauptansicht zu ermitteln.

3. Zeichnen Sie mithilfe der realen Längen der einfachen Linie, der Kantenlängen der quadratischen Öffnung und der entsprechenden Bogenausbreitungslängen der runden Öffnung nacheinander die 1/4-Ausbreitungen.

Wo der Übergangsteil des Vierkantrohrs dem Rundrohr gegenüberliegt, muss eine Vierkant-Rund-Verbindung vorhanden sein. Die Vierkantöffnung kann quadratisch oder rechteckig sein, die Rundöffnung kann in der Mitte, an einer Seite oder in einer Ecke liegen. Daher kann die Form solcher Verbindungen variieren, die Methode zur Ermittlung der tatsächlichen Länge der Vierkant- und Rundverbindungen ist jedoch grundsätzlich dieselbe.

Methode des rechtwinkligen Dreiecks

Die Methode des rechtwinkligen Dreiecks ist eine häufig verwendete Methode zum Bestimmen der tatsächlichen Länge.

Das Prinzip der Methode des rechtwinkligen Dreiecks und die Zeichenmethode: Das folgende Diagramm (a) ist das Hauptdiagramm der Methode des rechtwinkligen Dreiecks für reelle Längen. Das Liniensegment AB ist nicht parallel zur Projektionsebene und seine Projektionen ab und a'b' geben nicht die reelle Länge wieder. In der ABba-Ebene wird eine Linie parallel zu ab durch Punkt A gezogen und schneidet Bb im Punkt B1, wodurch das rechtwinklige Dreieck ABB1 entsteht. In diesem Dreieck kann die reelle Länge der Hypothenuse AB des rechtwinkligen Dreiecks ermittelt werden, indem die Längen der beiden rechtwinkligen Seiten AB1 und BB1 bekannt sind. Und die Längen von AB1 und BB1 ergeben sich im Projektionsdiagramm als AB1 = ab, BB1 = b'b1′ oder BB1 = b'bx – a'ax. Kennt man diese beiden rechtwinkligen Seiten, kann man das gesuchte rechtwinklige Dreieck eindeutig zeichnen.

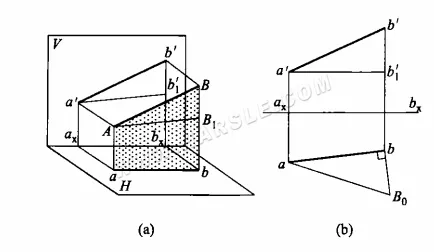
Abbildung (b) oben zeigt die Verwendung der rechtwinkligen Dreieckmethode zum Bestimmen der tatsächlichen Länge. Die Projektionen der Linie AB werden als ab und a'b' bezeichnet. Um die tatsächliche Länge von AB zu bestimmen, können Sie zunächst eine horizontale Linie durch den Punkt a' ziehen, die Linie bb' im Punkt b1' kreuzen und die Länge einer rechtwinkligen Kante von bb1' ermitteln. Zeichnen Sie dann von oben eine weitere rechtwinklige Kante von ab, ziehen Sie die vertikale Linie durch den Punkt b und schneiden Sie bB0 = b'b1', um die Verbindung zu aB0 herzustellen. Dies ist die tatsächliche Länge des Liniensegments.

Beispiel: Das folgende Diagramm zeigt eine kleine und eine große quadratische Mundverbindung. Versuchen Sie, die tatsächliche Länge ihrer Hauptlinie AC und Hilfslinie BC zu ermitteln.

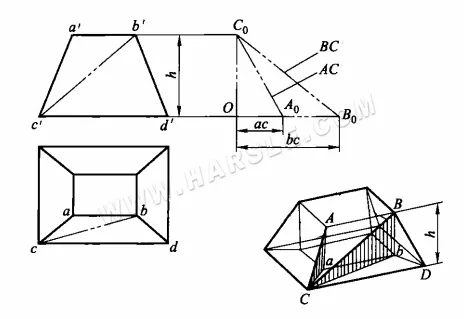
Aus der Abbildung ist ersichtlich, dass die tatsächliche Länge AC in einem rechtwinkligen Dreieck mit aC und Aa als den beiden rechtwinkligen Seiten zu finden ist, während die tatsächliche Länge BC im rechtwinkligen Dreieck BbC zu finden ist. In beiden Dreiecken ist Aa = Bb = h, was der Höhe der Verbindung entspricht. Die beiden anderen rechtwinkligen Seiten aC und bC entsprechen den Projektionen ac und bc von AC bzw. BC in der Draufsicht. Auf diese Weise können die tatsächlichen Längen von AC und BC wie folgt ermittelt werden.

1. Bilden Sie einen rechten Winkel B0OC0.

2. Achsenabschnitte OA0 und OB0 auf der horizontalen Seite dieses rechten Winkels, die in der Draufsicht jeweils ac und bc entsprechen, und Achsenabschnitte OC0 auf der vertikalen Seite, die in der Hauptansicht der Höhe h entsprechen.

3. Verbinden Sie C0A0 und C0B0, dann sind die Hypothenusen C0A0 und C0B0 die tatsächlichen Längen der gesuchten AC und BC.

Die rechtwinklige Trapezmethode

Die Methode des rechtwinkligen Trapezes ist auch eine gängige Methode zum Ermitteln realer Längen.

Das Prinzip der rechtwinkligen Trapezmethode zur Ermittlung realer Längen und die Zeichenmethode: Das folgende Diagramm zeigt das Prinzip der Anwendung der rechtwinkligen Trapezmethode zur Ermittlung realer Längen. Die allgemeine Lage der Linie AB in der V- und H-Fläche kann nicht die reale Länge wiedergeben, aber die beiden Endpunkte der Linie AB und der Abstand zwischen der V-Fläche (Aa und Bb) können auf der H-Fläche ermittelt werden. Ebenso können die beiden Punkte A und B sowie der Abstand zwischen der H-Fläche (Aa und Bb) auf der V-Fläche ermittelt werden. Basierend auf diesem Prinzip kann die reale Länge der Linie AB mithilfe der rechtwinkligen Trapezmethode ermittelt werden. Es gibt zwei spezielle Methoden zur grafischen Darstellung realer Längen.

1. Verwenden Sie die orthographische Projektion der tatsächlichen Länge der Linie AB: Die orthographische Projektion von AB a'b' als Unterkante des rechtwinkligen Trapezes, von den beiden Punkten a' und b' jeweils eine vertikale Linie nach oben, die die Längen von Aa' und Bb' abfängt und mit AB verbindet, ist die gewünschte Länge.

2. Die Verwendung der horizontalen Projektion der tatsächlichen Länge des Liniensegments AB: Die horizontale Projektion von AB dient als Unterkante eines rechtwinkligen Trapezes. Von den beiden Punkten a und b wird jeweils eine vertikale Linie nach oben gezogen. Die Längen von Aa und Bb werden abgeschnitten und AB wird wie gewünscht verbunden.

Beispiel: Die folgende Abbildung zeigt eine Hufeisenverformungsverbindung. Ihre obere und untere Öffnung sind Kreise, aber die beiden Kreise sind nicht parallel und haben nicht den gleichen Durchmesser. Versuchen Sie, aus ihrer Linienlänge und ihrem Ausdehnungsdiagramm ein rechtwinkliges Trapez zu erstellen.

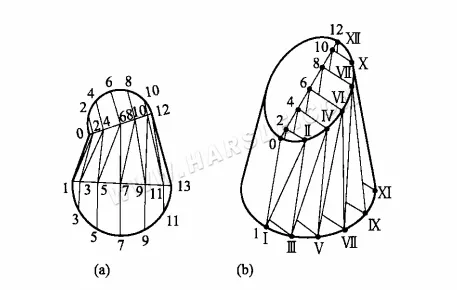
Aus der obigen Abbildung (a) ist ersichtlich, dass die Oberfläche keine Kegelfläche ist. Um das Ausdehnungsdiagramm zu erstellen, müssen Sie lediglich die Linien verwenden, die von und zur Oberfläche in mehrere Dreiecke zerlegen und nacheinander die tatsächliche Form dieser Dreiecke ermitteln. Die einzelnen Schritte zur grafischen Darstellung sind wie folgt.

1. Machen Sie 12 gleiche Teile des oberen und unteren Mundes und teilen Sie die Oberfläche in 24 Dreiecke auf, wie im Diagramm gezeigt.

2. Ermitteln Sie die tatsächlichen Längen der Linien Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII und erstellen Sie dann die tatsächliche Form der Dreiecksreihe.

Wenn in solchen Beispielen die Rotationsmethode oder die Methode des rechtwinkligen Dreiecks zur Ermittlung der tatsächlichen Länge verwendet wird, muss die Projektion des Liniensegments auf die Draufsicht erfolgen. Da die Oberseite der Hufeisenverformungsverbindung und die horizontale Projektionsebene geneigt sind, wird die Oberseite in der Draufsicht als Ellipse reflektiert. Offensichtlich sind diese beiden Methoden zur Erweiterung der Karte schwieriger. Zu diesem Zeitpunkt ist es angebracht, die Methode des rechtwinkligen Trapezes zu verwenden.

So wird beispielsweise in der obigen Abbildung (b) die gefaltete Oberfläche Ⅰ-1-Ⅱ-2-Ⅲ-3…XII-12 gestreckt, bis die unten gezeigte Abbildung entsteht. Dann folgt die Abbildung über der Faltlinie Ⅰ-Ⅱ-Ⅲ…XII, also die tatsächlichen Längen der Linien Ⅰ-Ⅱ, Ⅱ-Ⅲ, …, Ⅵ-VII usw. Diese Methode zum Ermitteln der tatsächlichen Längen ist die Methode des rechtwinkligen Trapezes.

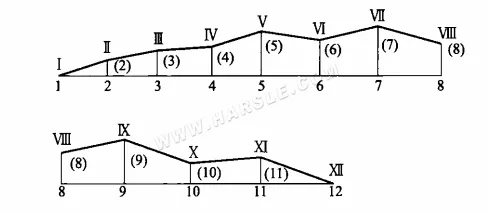
Wie aus der Diagrammmethode ersichtlich ist, basiert die Methode des rechtwinkligen Trapezes ebenfalls auf der Projektion einer schrägen Linie als Basis, wobei der Abstand der beiden Endpunkte der schrägen Linie von derselben Projektionsebene wie die beiden rechtwinkligen Seiten ist. Nach der Bildung eines rechtwinkligen Trapezes wird dann die Hypothenuse des rechtwinkligen Trapezes, d. h. die tatsächliche Länge der gewünschten Linie, berechnet. Das rechtwinklige Dreieck kann als Sonderfall der Methode des rechtwinkligen Trapezes betrachtet werden, bei dem die Länge der rechtwinkligen Seite gleich Null ist.

Mit der obigen Methode werden die beiden Seitenlinien jedes Dreiecks auf der Oberfläche der Hufeisenverformungsverbindung ermittelt, wobei die andere Seite der Länge der oberen und unteren kreisförmigen Öffnung entspricht, die dem entfalteten Bogen entspricht. Auf diese Weise kann mit der Methode der Dreiecke mit drei bekannten Seiten eine Reihe von Dreiecken erstellt werden, die so angeordnet werden, dass das folgende Diagramm der Hufeisenverformungsverbindung entsteht.

Gesichtsänderungsmethode

Neben den oben genannten Methoden zur Ermittlung der tatsächlichen Länge der Linie gibt es auch die gängige Methode zur Änderung der Oberfläche.

Das Prinzip der Methode zur Änderung der Oberfläche für die tatsächliche Länge und die Zeichenmethode: Das Prinzip der Methode zur Änderung der Oberfläche besteht darin, das Raumsegment unverändert zu lassen und eine weitere neue Projektionsfläche zu erstellen, um es parallel zum gewünschten Segment und senkrecht zum ursprünglichen Segment zu gestalten. Die Projektion des Segments auf die neue Projektionsfläche spiegelt seine tatsächliche Länge wider. Das obige Diagramm zeigt eine schematische Darstellung der tatsächlichen Länge eines Liniensegments.

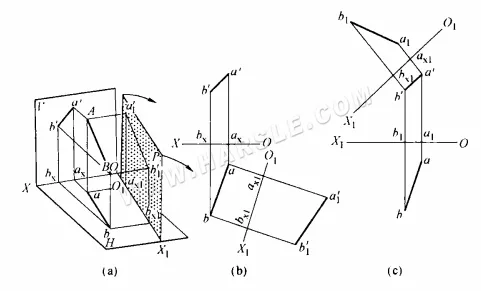
Wie aus dem obigen Diagramm (a) ersichtlich, verläuft die Strecke AB nicht parallel zu den Projektionsebenen H und V und ihre Projektion spiegelt nicht die tatsächliche Länge wider. Die neue Projektion a1'b1′ spiegelt die tatsächliche Länge von AB wider. Eine weitere Analyse des in Abbildung (a) dargestellten Raums ergibt die folgenden Projektionsbeziehungen für die Oberflächenänderungsmethode.

1. Da die neue Projektionsfläche P parallel zu AB und senkrecht zur H-Ebene ist, ist die Schnittlinie zwischen der neuen Projektionsfläche P und der H-Ebene, O1X1 (die sogenannte neue Projektionsachse), notwendigerweise parallel zur H-Ebenen-Projektion ab der Linie AB, O1X1 // ab, wie in der H-Ebenen-Projektion widergespiegelt.

2. Da die P- und V-Flächen gleichzeitig senkrecht zur H-Fläche stehen, müssen die Abstände der Projektion a1'b1′ der P-Fläche auf O1X1 und der Abstand der Projektion a'b' der V-Fläche auf OX gleichzeitig die senkrechten Abstände von den beiden Endpunkten A und B der Raumlinie zur H-Fläche widerspiegeln und sind einander gleich, a1ax1 = a'ax = Aa und b1'bx1 = Bb. Der Einfachheit halber wird die neu erstellte Projektion parallel zu AB verwendet. Die Projektion a1'b1′, die die tatsächliche Länge widerspiegelt, wird als neue Projektion bezeichnet, die Projektion a'b', die ursprünglich nicht die tatsächliche Länge widerspiegelte, als alte oder Ersatzprojektion und die Projektion der H-Ebene, die gleichzeitig senkrecht zu ihnen steht, als invariante Projektion. Auf diese Weise kann diese Projektionsbeziehung für die Ersatzflächenmethode so ausgedrückt werden, dass der Abstand der neuen Projektion zur neuen Achse gleich dem Abstand der alten Projektion zur alten Achse ist.

3. Da sowohl die P- als auch die V-Oberfläche senkrecht zur H-Oberfläche stehen, muss die Verbindung zwischen der P-Projektion und der H-Projektion an jedem Punkt der Linie senkrecht zur neuen Projektionsachse O1X1 stehen. Die Linie zwischen der invarianten Projektion und der alten und neuen Projektion steht nach dem Entfalten senkrecht zur alten bzw. neuen Projektionsachse.

In Übereinstimmung mit der obigen Projektionsbeziehung der Permutationsmethode sollten die Graphikschritte sein

1. Machen Sie die neue Projektionsachse O1X1 wie in (b) oben gezeigt parallel zu ab.

2. Zeichnen Sie eine senkrechte Linie durch die Punkte a und b zur O1X1-Achse und schneiden Sie O1X1 an den Punkten ax1 und bx1.

3. Verschieben Sie die Projektionen a' und b' der V-Ebene auf die OX-Achse zur neuen Projektionsebene, messen Sie ax1a1'=axa' und bx1b1'=bxb' auf den vertikalen Linien.

4. Verbinden Sie die Punkte a1′ und b1′, die neue Projektion a1'b1′ der Linie AB, die die tatsächliche Länge von AB widerspiegelt.

Beispiel: Das folgende Diagramm zeigt die Verwendung der Methode der Hilfsprojektionsebene, um die tatsächliche Form eines zylindrischen Abschnitts zu ermitteln.

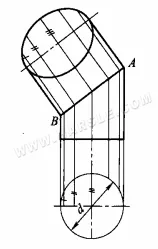
Die Schritte in der Zeichnung sind wie folgt.

1. Erstellen Sie eine Haupt- und eine Draufsicht, indem Sie die Draufsicht durch 1/2 des Kreisumfangs in 6 gleiche Teile teilen.

2. Zeichnen Sie eine vertikale Linie nach oben durch den äquidistanten Punkt, um die Position der Primlinie in der Hauptansicht anzugeben.

3. Zeichnen von Senkrechten nach unten von den äquidistanten Punkten, um die untere Mittellinie zu schneiden, die Breite zwischen den einfachen Linien des Abschnitts

4. Zeichnen Sie senkrechte Linien durch die Schnittpunkte der Linien auf der schrägen Öffnung des Abschnitts zur langen Achse parallel zur schrägen Öffnung des Abschnitts und zeichnen Sie dann den Abstand zwischen den gleich weit entfernten Punkten in der Draufsicht und der Mittellinie des unteren Kreises wiederum zu den Punkten in der Sekundäransicht gemäß der Regel der „gleichen Breite“.

5. Verbinden Sie die Punkte, um eine solide Ellipse des Abschnitts zu erstellen.

Das folgende Diagramm zeigt die Verwendung der Methode der Hilfsprojektionsebene, um die tatsächliche Form des Orthokonusabschnitts zu ermitteln. Die Diagramme ①, ②, … (7) geben die Reihenfolge der Zeichen- und Verbindungslinien an.

Im Allgemeinen ist es nicht notwendig, Linien auf der Kegeloberfläche zu zeichnen, um die tatsächliche Form des Kegelschnitts zu erhalten. Es ist jedoch besser, die Schusskreismethode zu verwenden, wie in der obigen Abbildung gezeigt. Um die Linien deutlich zu machen, werden die drei Schritte des Diagramms in diesem Beispiel separat gezeichnet. Das eigentliche Diagramm muss nicht getrennt werden. Die Schritte sind wie folgt.

1. Schusskreise: Die Projektionslinie des Abschnitts ist in 6 gleiche Teile unterteilt; die horizontale Linie der oben genannten gleichen Punkte wird mit der Konturlinie geschnitten; die vertikale Linie wird von jedem Schnittpunkt auf der Konturlinie nach unten gezeichnet und schneidet sich am Boden des Kegels; die Schusskreise werden wiederum mit der Mitte des O-Kreises gezeichnet, siehe Abbildung (a) oben.

2. Draufsicht des Querschnitts: Indem man in der Hauptansicht eine vertikale Linie nach unten durch jede Äquivokation der Querschnittslinien zieht, die den entsprechenden Breitenkreis schneidet, erhält man eine Reihe von Schnittpunkten; durch Verbinden der Schnittpunkte erhält man die Draufsichtprojektion des Querschnitts, siehe Abbildung (b) oben.

3. So ermitteln Sie die tatsächliche Form des Abschnitts: Zeichnen Sie eine Ellipse parallel zur Längsachse des Abschnitts 1″7″. Zeichnen Sie senkrechte Linien von jedem gleichen Punkt des Abschnitts 1~7 zur Längsachse 1″7″. Zeichnen Sie gemäß dem Prinzip der gleichen Breiten eine Reihe von Breiten a, b, c, d und e des Abschnitts in der Draufsicht auf die Hilfsprojektion, sodass die Punkte 2″, 3″, 4″, 5″ und 6″ entstehen. Verbinden Sie die Punkte, d. h. die tatsächliche Form des konischen Abschnitts, siehe Diagramm (b) oben. Abbildung (c) oben.

Das folgende Diagramm zeigt die Verwendung der Methode der Hilfsprojektionsfläche zum Ermitteln der tatsächlichen Form des schiefen Kegelschnitts.

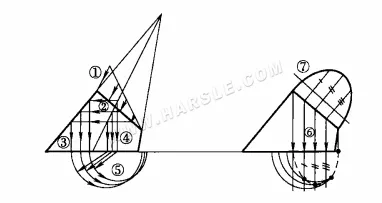
Die Verwendung der Hilfsansicht für die tatsächliche Form des schrägen Kegelschnitts ähnelt der des orthogonalen Kegelschnitts. Der schräge Kegel hat jedoch die Eigenschaft, dass seine Spitze und seine Achse zu einer Seite geneigt sind, sodass die Mittelpunkte mehrerer Schusskreise nicht am selben Punkt auf derselben Achse liegen. Daher wird anstelle konzentrischer Kreise ein Kegel mit einem Mittelpunkt für jeden Schusskreis erstellt. Diese Funktion lässt sich durch Befolgen der drei oben beschriebenen Schritte zum Zeichnen der Hilfsansicht eines Volumenkörpers erlernen.

Die einzelnen Zeichenschritte sind wie folgt.

1. Für den Schusskreis: die Schnittlinie durch 4 gleiche Teile; durch gleiche Punkte der Horizontalen, die sich mit der Höhenlinie schneidet; von der Höhenlinie über die Punkte nach unten zur Vertikalen, die sich mit dem Bodenkreis schneidet; durch gleiche Punkte der Horizontalen und die Achsenschnittpunkte für den Schusskreis von der Mitte zum Kreismittelpunkt zum Bodenkreis; jeweils den Mittelpunkt des Schusskreises und den entsprechenden Radius für den Schusskreis.

2. Die Draufsicht des Abschnitts: Durch die Hauptansicht der Abschnittslinien jeder Zweideutigkeit, der nach unten führenden vertikalen Linien und der entsprechenden Schnittpunkte des Breitenkreises entsteht eine Reihe von Schnittpunkten. Zusammen mit den Schnittpunkten erhalten Sie die Draufsicht der Abschnittsprojektion.

3. So erstellen Sie die tatsächliche Form des Abschnitts: Erstellen Sie entsprechend der Breite der in der Draufsicht ermittelten Abschnittsform eine halbe Hilfsansicht, um die halbe tatsächliche Form des schrägen Kegelabschnitts zu zeichnen.

Vergleich von Reallängenmethoden

Basierend auf der obigen Analyse kann ein einfacher Vergleich zwischen den vier Methoden zur Ermittlung der tatsächlichen Länge einer realen Linie durchgeführt werden.

Die Rotationsmethode berechnet die tatsächliche Länge, indem sie die Position der Figur im Raum ändert, ohne die Position der Projektionsebene zu ändern.

Die Permutationsmethode berechnet die tatsächliche Länge, indem die Position der Projektionsebene geändert wird, ohne die Position der Figur zu ändern.

Die Methode des rechtwinkligen Dreiecks und die Methode des rechtwinkligen Trapezes (die Methode des rechtwinkligen Dreiecks kann als Sonderfall der Methode des rechtwinkligen Trapezes angesehen werden) lösen die Linie mit der reellen Länge, indem weder die Position der Raumfigur noch die Position der Projektionsebene geändert wird.