In my exploration of hydraulic systems, I’ve often been fascinated by how a hydraulic press multiplies force to perform heavy-duty tasks efficiently. This mechanical marvel operates on the principle of Pascal’s law, which states that pressure applied to a confined fluid is transmitted undiminished in all directions. Understanding how a hydraulic press multiplies the force not only reveals the brilliance of its design but also highlights its applications in various industries. In this article, I will delve into the mechanics behind the hydraulic press and explain how it can amplify force to accomplish demanding tasks with ease.

Pascal’s law:

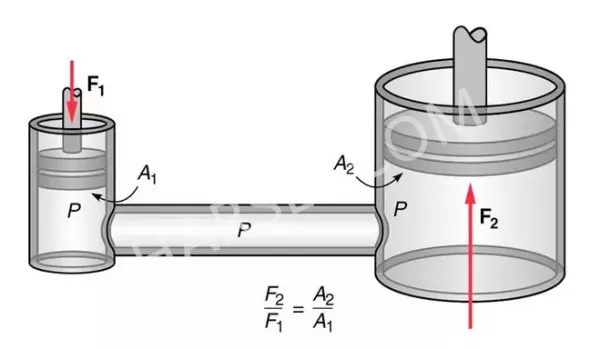
Pressure P is the same everywhere there. Pressure P applied on area A2, that means force F2 = P x A2, is much more than force F1 = P x A1 .

Where:

• P is the pressure in the hydraulic system
• F1 is the input force on the small piston
• A1 is the surface area of the small piston
• F2 is the output force on the large piston
• A2 is the surface area of the large piston

This principle is described by Pascal’s Law (also known as Pascal’s Principle), which states that any change in pressure applied to a confined, incompressible fluid is transmitted equally and undiminished throughout the fluid in all directions. As a result, the same pressure acts on all internal surfaces of the system.

A common practical example of Pascal’s Law is lifting a car using a hydraulic press or jack. Although a person applies only a relatively small force by hand, the hydraulic system converts that force into a much larger lifting force.

Hydraulic systems rely on the fact that liquids are essentially incompressible (ignoring extreme, theoretical pressure levels). This means that when a volume of fluid is displaced at one point, the same volume must move elsewhere in the system.

For example, consider a system with:

• A small piston with a diameter of 10 mm
• A large piston with a diameter of 100 mm
• Both pistons connected by a sealed pipe filled with hydraulic oil

If the small piston is pushed downward by 100 mm, the displaced oil volume forces the large piston to move upward by only 1 mm. This difference in movement occurs because the surface area of the large piston is 100 times greater than that of the small piston. However, in exchange for the reduced movement, the output force on the large piston becomes 100 times greater than the input force (assuming friction and losses are neglected).

In other words, while distance is reduced, force is amplified, and the total energy in the system remains balanced.

Furthermore, if the connecting pipe is equipped with a one-way check valve, the system can operate as a hydraulic pump. Each stroke of the small piston adds pressure to the system, causing the large piston to move upward incrementally. With every pump stroke, the large piston advances another 1 mm, continuously applying a force that is 100 times stronger than the input force.

This operating principle is widely used in hydraulic presses, jacks, bending machines, and other heavy-duty industrial equipment, where large forces are required but only limited manual or motor-driven input is available.

Here’s how it works step by step in the context of a hydraulic press

Two Pistons:

A hydraulic press typically consists of two pistons with different sizes, connected by a cylinder filled with fluid—usually oil.

Applying Force on a Small Piston: 

When a force is applied to the smaller piston, it creates pressure in the fluid beneath it. Since the fluid is incompressible, this pressure is transmitted uniformly throughout the fluid.

Pressure Transmission: 

According to Pascal’s law, the pressure (defined as force per unit area,P=F/A)exerted on the small piston must be equal to the pressure exerted on the large piston. Therefore, if the small piston has a force F1 and area A1, and the large piston has a larger area A2, the pressure P in the system can be expressed as: P=F1/A1=F2/A2 

Where:

●F1 is the force applied to the input piston

●A1 is the area of the input piston

●F2 is the force exerted by the output piston

●A2 is the area of the output piston

Force Amplification:

Rearranging the equation:P=F1/A1=F2/A2

for F2 (the force exerted by the large piston)This shows that the force F2 is multiplied by the ratio of the areas of the two pistons. Since A2 is larger than A1, F2 is greater than F1.

Video