Prognozowanie promienia gięcia wewnętrznego podczas używania prasy krawędziowej
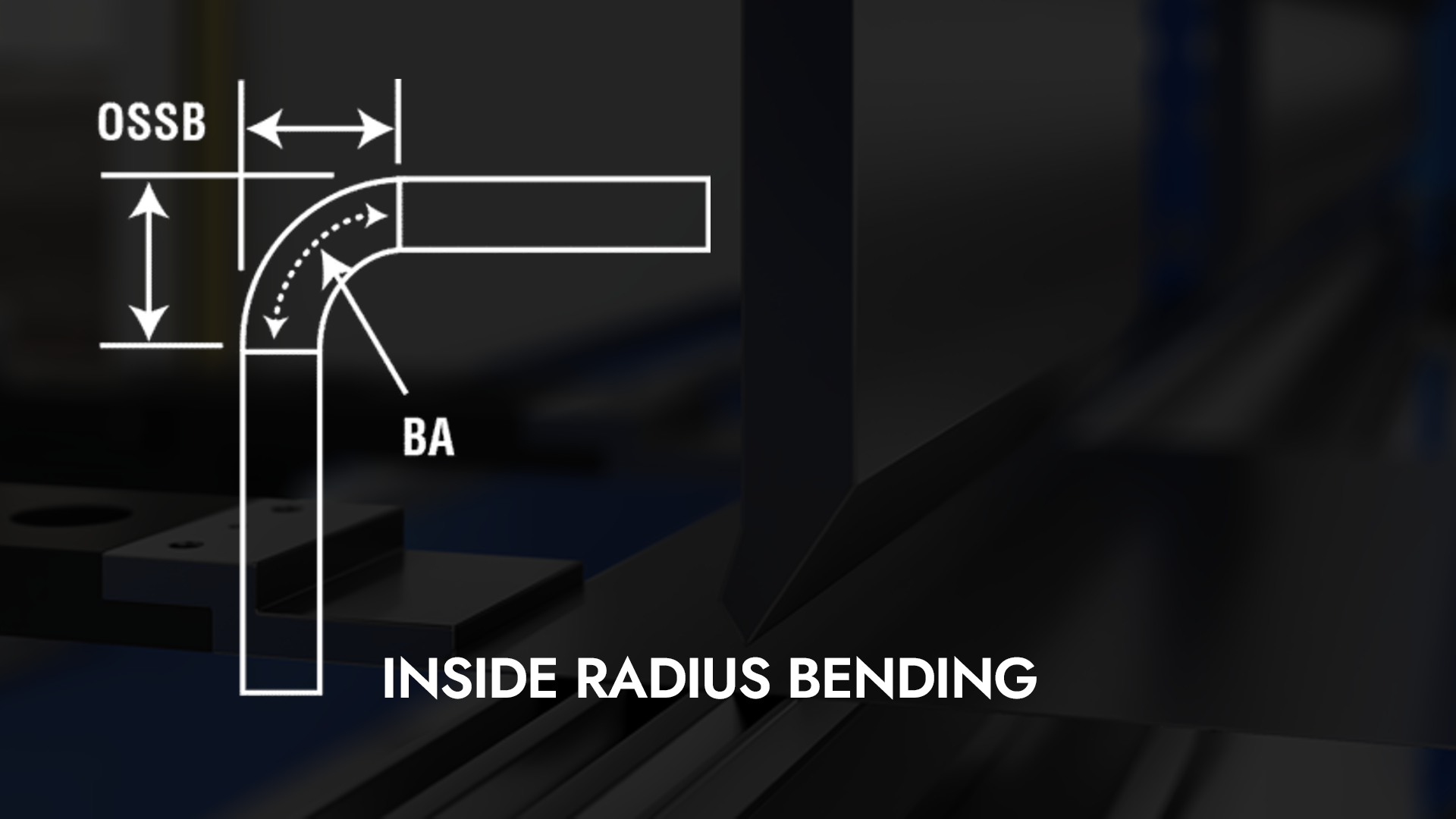
Gdy zagłębiam się w temat przewidywania Gięcie promienia wewnętrznego Korzystając z prasy krawędziowej, odkryłem, że zrozumienie zawiłości tego procesu może znacząco wpłynąć na jakość naszych projektów obróbki metali. Promień wewnętrzny odgrywa kluczową rolę w zapewnieniu precyzyjnych gięcia i osiągnięciu pożądanych rezultatów. W tym artykule podzielę się spostrzeżeniami i technikami, które pomogły mi skutecznie przewidzieć promień wewnętrzny podczas korzystania z prasy krawędziowej, zwiększając zarówno wydajność, jak i dokładność naszych operacji. Dołącz do mnie, aby zgłębić ten istotny aspekt obróbki metali!
Przewidywanie promienia nigdy nie jest w stu procentach dokładne, ale to jest najlepsze, co można zrobić.
Aby przewidzieć wewnętrzny promień gięcia podczas formowania w powietrzu, można posłużyć się kilkoma ogólnie przyjętymi zasadami. Uzyskane wyniki są zazwyczaj wystarczająco dokładne, ale z pomocą kilku kalkulatorów dostępnych online można uzyskać jeszcze lepsze wyniki.
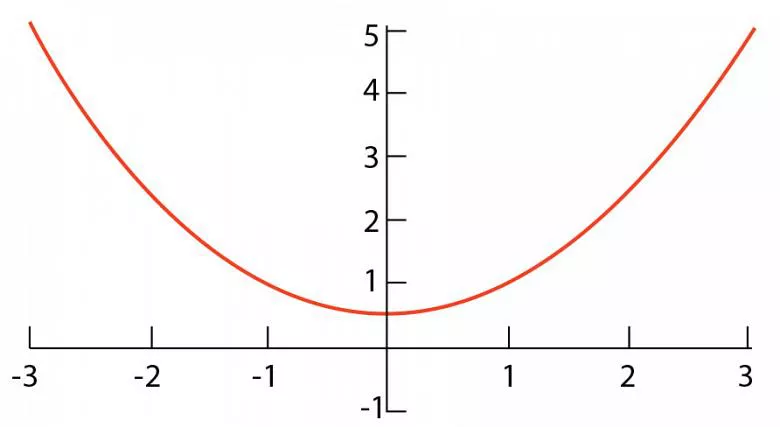
Często podczas formowania nie tworzymy prawdziwego promienia, lecz parabolę.
Jeśli w ostatnich miesiącach śledziłeś naszą dyskusję na temat promień gięcia I skąd się to bierze, witamy ponownie. Tak czy inaczej, zobaczmy, jak głęboka jest ta promienista królicza nora.
W poprzednich artykułach omówiłem różne praktyczne zasady, którymi posługują się operatorzy na hali produkcyjnej, aby wykonać swoją pracę. Zasady te mogą pomóc w dokładnym przewidzeniu wewnętrznego promienia gięcia, ale można je jeszcze bardziej udoskonalić.
Jaką to robi różnicę?
Rozważmy typową sytuację, w której stosujemy regułę 20 procent, która mówi, że promień gięcia w powietrzu stanowi procent otworu matrycy, 20 do 22 procent w przypadku stali nierdzewnej i około 16 procent w przypadku stali walcowanej na zimno 60 KSI, która jest naszym materiałem bazowym.
Załóżmy, że gniesz miękkie aluminium o gęstości 13 KSI za pomocą matrycy o szerokości 0,984 cala i stempla o promieniu 0,032 cala. Na początek obliczasz wewnętrzny promień gięcia na 16% otworu matrycy i wynosi on 0,157 cala, chociaż dotyczy to materiału o gęstości 60 KSI, więc musisz dostosować się do rodzaju materiału. Tymczasem, obliczając, czy gięcie będzie ostre, okazuje się, że minimalny promień, zanim stempel o średnicy 0,032 cala zacznie zaginać linię gięcia, wynosi 0,172 cala. Na koniec wykonujesz gięcie próbne, tylko po to, by stwierdzić, że rzeczywisty promień wynosi 0,170 cala.
Masz promień 0,157 cala obliczony na podstawie reguły 20 procent, a następnie promień 0,172 cala z obliczeń dla ostrych zagięć. To różnica w promieniu 0,015 cala. Niewiele mówisz? W tym przypadku różnica po uwzględnieniu odliczenia za zagięcie może sięgać 0,009 cala na zagięcie.
Czy kiedykolwiek zbudowałeś część z czterema bocznymi kołnierzami i czterema dodatkowymi u góry, tylko po to, by odkryć, że jeden narożnik jest idealny, dwa narożniki są średnio satysfakcjonujące, a jeden wygląda po prostu okropnie? Dlaczego tak się dzieje? Niewielki błąd w obliczeniach gięcia spowodowany rozbieżnościami w obliczeniach wewnętrznego promienia gięcia ma ogromne znaczenie, jeśli chcesz uzyskać idealne części za pierwszym razem.
Sercem każdej operacji gięcia jest promień wewnętrzny gięcia. Jeśli potrafisz obliczyć odliczenie od gięcia na podstawie rzeczywistych wyników, precyzja jest gwarantowana. Jedynym minusem tej teorii jest to, że często podczas formowania nie formujemy rzeczywistego promienia. Kształt, który formujesz, może być parabolą, symetryczną krzywą odbitą w lustrze, zazwyczaj w kształcie litery U, gdy jest zorientowany jak na rysunku 1. A ostateczny promień, jaki uzyskasz, jest wynikiem sprężystości.
- Efekty sprężynowania
Jak więc przewidzieć najdokładniejszy promień gięcia i prawidłową dedukcję gięcia? Aby wykonać to ręcznie, matematyka jest bardzo skomplikowana, więc nie będę się w to zagłębiać. Zamiast tego po prostu skorzystamy z dwóch różnych kalkulatorów internetowych.
Pierwszy z nich znajduje się na stronie www.harsle.com. Kliknij „The Complete Circular Arc Calculator”. Zwróć uwagę, że etykieta „Szerokość łuku” w kalkulatorze jest taka sama jak szerokość wykrojnika, a „Kąt podparty łukiem” jest taki sam jak uwzględniony kąt gięcia.
Upewnij się, że ustawienia wymiarów kalkulatora są prawidłowe dla używanych danych — cali, stóp, milimetrów itd. Pamiętaj, że po kliknięciu Enter otrzymane odpowiedzi są czysto matematyczne i nie uwzględniają wytrzymałości materiału na rozciąganie.
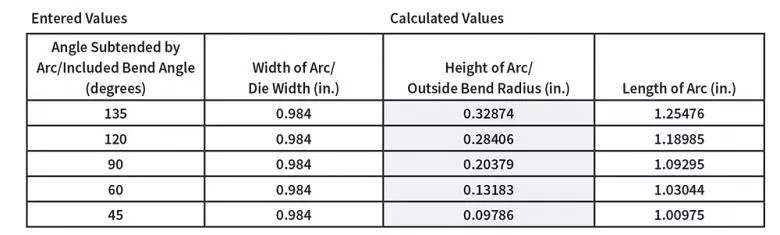
Jak pokazano w tym obliczeniu z The Complete Circular Arc Calculator na stronie www.harsle.com, wraz ze wzrostem kąta gięcia wzrasta również promień (wysokość łuku).
Informacją, której szukamy w kalkulatorze, jest wysokość łuku, która odpowiada zewnętrznemu promieniowi gięcia. Znajdźmy wartość dla naszej wartości bazowej, stali walcowanej na zimno 60-KSI o grubości 0,125 cala, używając matrycy o szerokości 0,984 cala. Należy pamiętać, że omawiamy formowanie powietrzne, więc kąt matrycy nie będzie miał znaczenia; może to być matryca kanałowa, ostra lub V. Liczy się szerokość.
Najpierw wprowadźmy kąt rozluźnienia — te 90 stopni, które chcemy osiągnąć.
Wprowadzone wartości
Kąt oparty na łuku (wliczając kąt zgięcia): 90 stopni
Szerokość łuku (szerokość matrycy): 0,984 cala.
Wartość obliczona
Wysokość łuku (zewnętrzny promień gięcia): 0,20379 cala.
Te obliczenia nie uwzględniają jednak sprężystości. W naszym przykładzie użyjemy wartości 1 stopnia dla sprężystości, która występuje, gdy mamy przybliżoną relację 1:1 między grubością materiału a wewnętrznym promieniem gięcia. Po zwolnieniu nacisku formującego przez stempel, materiał sprężystie powraca o 1 stopień, więc aby to skompensować, używamy teraz kąta gięcia 89 stopni. Ponownie korzystając z kalkulatora łuku kołowego The Complete Circular Arc Calculator na harsle.com, wprowadzamy następujące dane:
Wprowadzone wartości
Szerokość łuku (szerokość matrycy): 0,984 cala.
Kąt podparty łukiem (wliczając kąt zgięcia): 89 stopni
Wartość obliczona
Wysokość łuku (zewnętrzny promień gięcia): 0,201 cala.
Teraz bierzemy wartość wysokości łuku dla naszego nowego kąta gięcia i podstawiamy ją do następującego wzoru:
Wysokość łuku – (2 × Grubość materiału2) = Promień wewnętrzny
0,201 – (2 × 0,01562) = Wewnętrzny promień gięcia
0,201 – 0,031 = 0,170 cala. Promień gięcia wewnętrznego
Należy zauważyć, że podejście oparte na wysokości łuku różni się od podejścia zastosowanego w poprzednim artykule „Podstawy gięcia”, gdzie użyliśmy długości łuku. W poprzednim miesiącu obliczyliśmy promień wewnętrzny na podstawie szerokości otworu matrycy; tym razem używamy konkretnego promienia.
W zeszłym miesiącu obliczyliśmy promień 0,136 cala, a teraz obliczyliśmy promień wewnętrzny inną metodą i otrzymaliśmy 0,170 cala – różnicę 0,034 cala. Co więcej, gdybyśmy zastosowali regułę 20 procent (ponownie, dla stali walcowanej na zimno o gęstości 60 KSI promień oblicza się na około 16 procent szerokości matrycy), otrzymalibyśmy promień wewnętrzny 0,157 cala – w połowie odległości między tymi dwoma poprzednimi pomiarami. To są różne sposoby obliczania promienia, dające nieco odmienne rezultaty. Ale tak, królicza nora jest głębsza!
- Parabola i ostre zakręty
Jeśli użyjesz promienia wykrojnika równego lub mniejszego od minimalnego promienia ostrego gięcia dla części formowanej powietrzem, nie utworzysz już promienia w części (aby dowiedzieć się więcej o ostrych gięciach, w sekcji „Zamiast tego utworzysz parabolę”). W efekcie wciągasz inną długość łuku do otworu matrycy.
Aby przewidzieć, jak uformuje się ta parabola, możemy skorzystać z innego kalkulatora online:
Wprowadzamy promień zewnętrzny i szerokość matrycy, aby obliczyć długość łuku paraboli. Wartość wysokości w tym kalkulatorze online jest równa zewnętrznemu promieniowi gięcia, a wartość szerokości jest równa szerokości matrycy:
Wprowadzone wartości
Wysokość: (promień zewnętrzny): 0,201 cala.
Szerokość (szerokość matrycy): 0,984 cala.
Wartość obliczona
Długość łuku: 1,0845 cala.
Tutaj głębokość paraboli (lub wysokość łuku) wynosi 0,201 cala, a długość łuku paraboli to 1,0845 cala. Zapamiętaj te wartości. Wracając teraz do kalkulatora łuku kołowego na stronie www.harsle.com, wprowadzamy długość łuku równą 1,0845 cala, a szerokość matrycy równą 0,984 cala.
Wprowadzone wartości
Długość łuku: 1,0845 cala.
Szerokość łuku (szerokość matrycy): 0,984 cala.
Obliczone wartości
Wysokość łuku (zewnętrzny promień gięcia): 0,195 cala.
Kąt podparty łukiem
(wliczony kąt gięcia): 86,679 stopni
Kiedy to zrobisz, zobaczysz, że wysokość łuku (czyli promień zewnętrzny) wynosi 0,195 cala, czyli jest nieco mniejsza niż promień zewnętrzny 0,201 cala z poprzedniego kalkulatora, który nie uwzględniał efektu paraboli. Wiedząc to, możemy śmiało powiedzieć, że promień wewnętrzny zmniejsza się, gdy formowana jest parabola, co ma miejsce, gdy używany jest promień stempla mniejszy niż minimalny promień ostrego gięcia. Należy zauważyć, że parabola wymaga również większego kąta gięcia, aby uzyskać pożądany kąt gięcia rozluźnionego; przeszliśmy z 89 do 86,68 stopnia z uwzględnieniem kąta gięcia, co daje dodatkowe 2,32 stopnia sprężystości. Należy również zauważyć, że promień wewnętrzny części nie będzie mniejszy niż promień czoła stempla.
- Kąt i promienie gięcia
Pamiętaj, że każda zmiana promienia powoduje zmianę kąta gięcia. Jeśli wprowadzimy szerokość matrycy i uwzględnimy kąt gięcia na stronie www.harsle.com, otrzymamy wyniki pokazane na rysunku 2.
Wyniki pokazują, że podczas formowania w powietrzu promień zmniejsza się wraz ze wzrostem kąta gięcia (z wyłączeniem ostrych zagięć).
Zależność kąta i promienia gięcia kończy się przy kątach mniejszych niż 28 stopni (152 stopnie uzupełniające), choć minimalny kąt może być większy w materiale o znacznym sprężystości.
Dzieje się tak częściowo dlatego, że minimalny kąt stempla prasy krawędziowej wynosi 28 stopni włącznie. Niemniej jednak, dalsze zamykanie zagięcia powyżej 28 stopni włącznie spowoduje pewien rodzaj spłaszczenia. Promień będzie zmniejszany, aż do osiągnięcia pożądanego kąta gięcia lub zakończenia operacji zaginania. (Na marginesie, w przypadku zagięcia zamkniętego promień wynosi zero, a odliczenie od zagięcia jest obliczane jako procent grubości materiału – 43 procent w idealnych warunkach, choć jest to operacja w dużej mierze zależna od operatora).
- Współczynnik wytrzymałości na rozciąganie
W poprzednim przykładzie do obliczeń użyliśmy 1 stopnia sprężystości. W przypadku stali niskowęglowej walcowanej na zimno o twardości 60 KSI średni stopień sprężystości wynosi 1 stopień lub mniej. A co z innymi materiałami?
W tym celu możemy przewidzieć sprężystość z rozsądną dokładnością, korzystając z poniższego wzoru, który wymaga przeliczenia wszystkich wartości na wartości metryczne. Należy pamiętać, że przewidywanie sprężystości nigdy nie jest w 100% dokładne. Jednak te wzory sprawdzają się całkiem dobrze.
[(Promień wewnętrzny w milimetrach/2)/
Grubość materiału w milimetrach] × Współczynnik rozciągania
Współczynnik rozciągania = wytrzymałość materiału na rozciąganie w PSI/60 000
Najpierw obliczmy sprężystość, tak jakbyśmy pracowali z materiałem bazowym 60-KSI o wewnętrznym promieniu gięcia wynoszącym 0,170 cala:
[(Promień wewnętrzny w milimetrach/2)/
Grubość materiału w milimetrach] × Współczynnik rozciągania
Grubość materiału: 0,125 cala × 25,4 = 3,175 mm
Promień gięcia wewnętrznego: 0,170 cala × 25,4 = 4,318 mm
(4.318/2) /3.175
2,159 mm /3,175 mm = 0,68 stopnia sprężynowania
W tym przykładzie zaokrąglimy to do 1 stopnia. Następnie możemy zastosować współczynnik rozciągania dla stali nierdzewnej 88-KSI 304.
Współczynnik rozciągania = wytrzymałość materiału na rozciąganie w PSI/60 000
88,000/60,000 = 1.466666
1,0 stopień × 1,466666
Daje nam to 1,46 stopnia dla stali nierdzewnej 88-KSI 304. Zaokrąglając, daje nam to szacowany współczynnik sprężystości 1,5 stopnia przy stosunku promienia wewnętrznego do grubości materiału 1:1.
- Powrót do kalkulatora
Teraz, gdy możesz oszacować sprężystość z rozsądnym poziomem dokładności, możesz ją skompensować. Aby określić kąt potrzebny do skompensowania sprężystości, wystarczy odjąć wartość sprężystości, jeśli pracujesz z kątami gięcia zawartymi, lub dodać tę wartość, jeśli używasz kątów gięcia uzupełniającego. Kalkulator łuku kołowego na stronie www.harsle.com działa z kątami gięcia zawartymi (oznaczonymi również jako „Kąt łuku wystający”).
Gdy znasz promień wewnętrzny — czyli rzeczywisty promień wewnętrzny, który pojawi się w gotowym elemencie — możesz wprowadzić wartość tego promienia do wzorów gięcia (patrz pasek boczny).
Wniosek
Prawidłowo prognozując promień wewnętrzny, możemy precyzyjnie obliczyć odliczenia od gięcia. Spośród kilku sposobów przewidywania promienia wewnętrznego, żaden nie jest idealny, ale ten jest chyba najlepszy. Mimo to, gięcie ma zbyt wiele zmiennych, aby osiągnąć 100-procentową dokładność.
W przypadku formowania pneumatycznego niezwykle ważne jest również, aby inżynier lub programista poinformował technika o zestawach narzędzi, z których zaprojektowano dane gięcie. Co więcej, technik musi zdawać sobie sprawę z absolutnego znaczenia korzystania z tych narzędzi dla uzyskania wysokiej jakości części.
W przyszłym miesiącu omówimy, jak obliczyć promień wewnętrzny gięcia, w którym zależność między promieniem wewnętrznym a grubością materiału jest bardzo duża – gięcia o dużym promieniu. Gięcia o dużym promieniu wiążą się z problemami z kątem i szerokością matrycy, wielokrotnym pękaniem i, oczywiście, bardzo dużym sprężystością.
Do króliczej nory jeszcze daleka droga, ale podróż warta jest zachodu.
Przegląd wzorów zginania
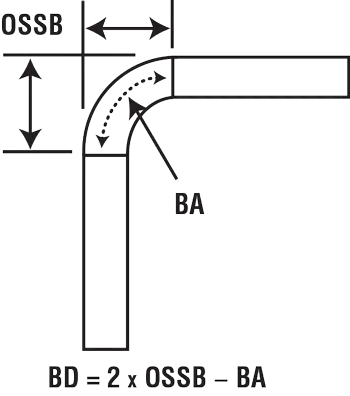
Wzory na naddatek na gięcie, odsunięcie zewnętrzne i odliczenie zagięć są dobrze znane, a każdą wartość można wykorzystać na różne sposoby do obliczenia układu płaskiego części.
Formuły
BA = [(0,017453 × Rp) + (0,0078 × Mt)]
× Stopnie gięcia uzupełniające
OSSB = [Styczna (stopień kąta zgięcia/2)]
× (Mt + Rp)
BD = (OSSB × 2) – BA
Klawisz
Rp = Promień czoła dziurkacza (dolny)
lub pływający promień wewnętrzny (formujący powietrze)
Mt = Grubość materiału
BA = Dodatek na zginanie
BD = Odliczenie zakrętu
OSSB = Cofnięcie zewnętrzne
0,017453 = π/180
0,0078 = współczynnik K × π /180
Współczynnik K = 0,446










America-Miami-Customer-Feeback-1.jpg)
Uzbekistan-Customer-Feedback1.png)
Kosovo-Customer-Feedback11.png)
Russia-Customer-Feedback.jpg)
Russia-Customer-Feedback-3.jpg)






