Previsão da curvatura do raio interno ao usar a prensa dobradeira
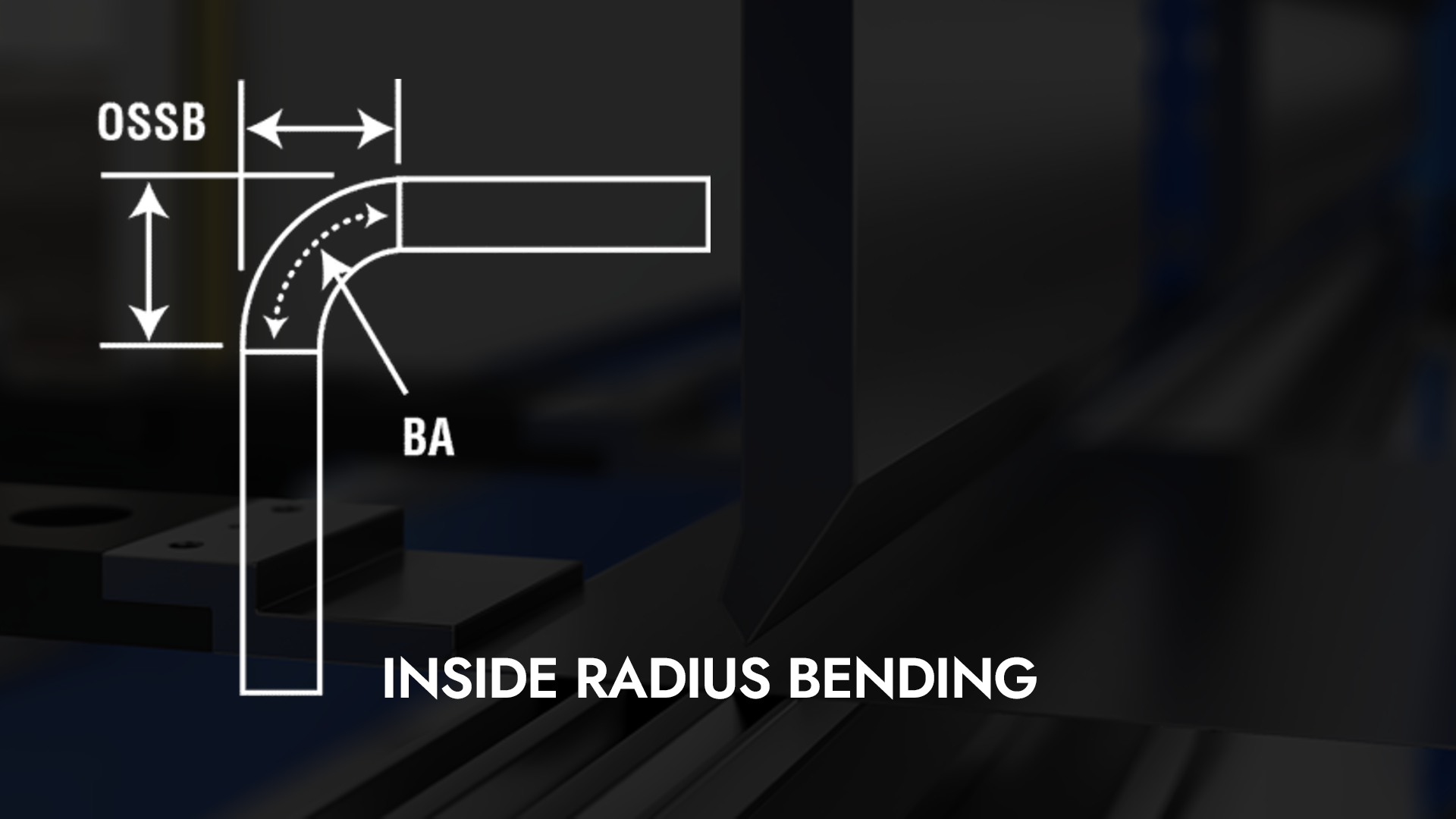
À medida que me aprofundo no tópico de Previsão Curvatura de raio interno Ao utilizar uma prensa dobradeira, descobri que entender as complexidades desse processo pode impactar significativamente a qualidade dos nossos projetos de fabricação de metais. O raio interno desempenha um papel crucial para garantir dobras precisas e alcançar os resultados desejados. Neste artigo, compartilharei insights e técnicas que me ajudaram a prever com eficácia o raio interno ao usar uma prensa dobradeira, aumentando a eficiência e a precisão em nossas operações. Junte-se a mim para explorarmos esse aspecto essencial da metalurgia!
Prever o raio nunca é 100% preciso, mas isso é o melhor que se pode conseguir.
Você pode usar algumas regras práticas comuns para prever a curvatura do raio de curvatura interno durante a conformação de ar, e os resultados obtidos geralmente são próximos o suficiente, mas com a ajuda de algumas calculadoras on-line, você pode chegar ainda mais perto.
Muitas vezes, durante a formação, não estamos formando um raio verdadeiro, mas sim uma parábola.
Se você tem acompanhado nossa discussão sobre raio de curvatura E de onde vem, bem-vindo de volta. De qualquer forma, vamos ver até onde vai essa toca de coelho de raio.
Em artigos anteriores, discuti várias regras práticas que os operadores usam na fábrica para realizar o trabalho. Essas regras podem aproximar sua previsão do raio de curvatura interno, mas você pode chegar ainda mais perto.
Que diferença isso faz?
Considere uma situação típica em que você usa a regra dos 20 por cento, que afirma que um raio de curvatura de ar se forma como uma porcentagem da abertura da matriz, 20 a 22 por cento para aço inoxidável e cerca de 16 por cento para aço laminado a frio de 60 KSI, nosso material básico.
Digamos que você esteja dobrando alumínio macio de 13 KSI com uma largura de matriz de 0,984 pol. e um punção com raio de 0,032 pol. Como ponto de partida, você calcula o raio de curvatura interno a 16% da abertura da matriz como 0,157 pol., embora isso seja para material de 60 KSI, então você precisará se adaptar ao tipo de material. Enquanto isso, ao calcular para ver se a dobra ficará acentuada, você descobre que o raio mínimo antes que o punção de 0,032 pol. comece a vincar a linha de dobra é de 0,172 pol. Por fim, você executa uma dobra de teste, apenas para descobrir que o raio real é de 0,170 pol.
Você tem o raio de 0,157 pol. calculado a partir da regra dos 20%, e depois tem o raio de 0,172 pol. dos seus cálculos de curva acentuada. Isso representa uma diferença de raio de 0,015 pol. Não é muita coisa, não é? Neste caso, a diferença, quando aplicada à dedução da curva, pode chegar a 0,009 pol. por curva.
Você já construiu uma peça com quatro flanges laterais e mais quatro flanges na parte superior, apenas para descobrir que um canto ficou perfeito, dois cantos ficaram medianamente satisfatórios e um ficou simplesmente horrível? Por que isso acontece? Um pequeno erro na dedução de dobra causado por discrepâncias nos cálculos do raio de curvatura interno faz uma grande diferença se você deseja peças perfeitas logo na primeira tentativa.
O cerne de qualquer operação de dobra é o raio interno da dobra. Se você puder calcular a dedução da dobra com base nos resultados reais, a precisão estará garantida. A única falha nessa teoria é que, muitas vezes, durante a conformação, não estamos formando um raio real. A forma que você está formando pode ser uma parábola, uma curva simétrica espelhada, geralmente em forma de U quando orientada como mostrado na Figura 1. E o raio final obtido é o resultado do retorno elástico.
- Efeitos de retorno elástico
Então, como podemos prever a curvatura mais precisa do raio interno e a dedução correta da curvatura? Para fazer isso manualmente, a matemática é complexa, então não vou entrar nesse assunto. Em vez disso, usaremos duas calculadoras online diferentes.
O primeiro está em www.harsle.com. Clique em "The Complete Circular Arc Calculator" (Calculadora de Arco Circular Completa). Observe que a largura do arco na calculadora é igual à largura da matriz, e o ângulo subtendido pelo arco é igual ao ângulo de curvatura incluído.
Certifique-se de que as configurações de dimensão da calculadora estejam corretas para os dados que você está usando — polegadas, pés, milímetros, etc. Observe que, quando clicamos em Enter, as respostas que obtemos são puramente matemáticas e não foram fatoradas para a resistência à tração do material.
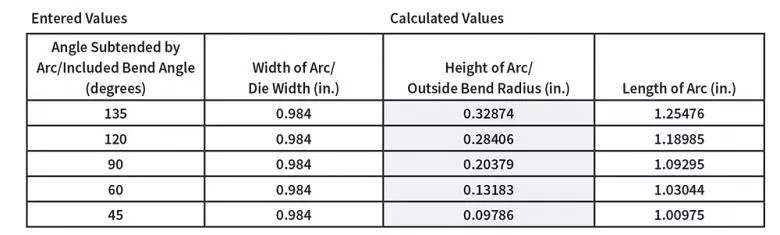
Conforme mostrado neste cálculo do The Complete Circular Arc Calculator em www.harsle.com, à medida que o ângulo de curvatura incluído aumenta, o raio (altura do arco) também aumenta.
A informação que procuramos na calculadora é a Altura do Arco, que equivale ao raio de curvatura externo. Vamos encontrar um valor para nossa linha de base, aço laminado a frio de 60 kJ, com 0,125 pol. de espessura, usando uma largura de matriz de 0,984 pol. Observe que estamos falando de conformação a ar, portanto, o ângulo da matriz não fará diferença; pode ser uma matriz de canal, aguda ou em V. É a largura que importa.
Primeiro, vamos entrar no ângulo relaxado — os 90 graus que queremos atingir.
Valores inseridos
Ângulo subtendido pelo arco (ângulo de curvatura incluído): 90 graus
Largura do arco (largura da matriz): 0,984 pol.
Valor Calculado
Altura do arco (raio de curvatura externo): 0,20379 pol.
No entanto, esses cálculos não levam em conta o retorno elástico. Para o nosso exemplo, usaremos um valor de 1 grau para o retorno elástico, que ocorre quando temos uma relação aproximada de 1 para 1 entre a espessura do material e o raio de curvatura interno. Após o punção liberar a pressão de conformação, o material retorna 1 grau, portanto, para compensar, agora usamos um ângulo de curvatura de 89 graus incluído. Novamente, usando a Calculadora de Arco Circular Completo em harsle.com, inserimos o seguinte:
Valores inseridos
Largura do arco (largura da matriz): 0,984 pol.
Ângulo subtendido pelo arco (ângulo de curvatura incluído): 89 graus
Valor Calculado
Altura do arco (raio de curvatura externo): 0,201 pol.
Agora pegamos o valor da Altura do Arco para nosso novo ângulo de curvatura e o inserimos na seguinte fórmula:
Altura do arco – (2 × Espessura do material2) = Raio interno
0,201 – (2 × 0,01562) = Raio de curvatura interno
0,201 – 0,031 = 0,170 pol. Raio de curvatura interno
Observe que esta abordagem da Altura do Arco é diferente da abordagem adotada na coluna Noções Básicas de Dobra do mês passado, quando usamos o Comprimento do Arco. No mês passado, calculamos um raio interno com base na largura da abertura da matriz; desta vez, estamos usando um raio específico.
No mês passado, calculamos um raio de 0,136 pol. e agora mesmo calculamos o raio interno usando um método diferente e chegamos a 0,170 pol. — uma diferença de 0,034 pol. Além disso, se usássemos a regra dos 20% (novamente, para aço laminado a frio de 60 kJ, o raio é calculado em cerca de 16% da largura da matriz), calcularíamos um raio interno de 0,157 pol. — a meio caminho entre as duas medições anteriores. Todas essas são maneiras diferentes de calcular um raio, com resultados ligeiramente diferentes. Mas, sim, a toca do coelho é mais profunda!
- Parábola e Curvas Acentuadas
Se você usar um valor de raio de punção igual ou menor que o raio mínimo de curvatura acentuada para conformação de ar de uma peça, você não estará mais criando um raio na peça (para mais informações sobre curvaturas acentuadas, consulte Em vez disso, você estará criando uma parábola. Você estará, na verdade, puxando um comprimento de arco diferente para dentro da abertura da matriz.
Para prever como essa parábola se formará, podemos recorrer a outra calculadora online:
Inserimos o raio externo e a largura da matriz para encontrar o comprimento do arco da parábola. O valor da altura nesta calculadora online é equivalente ao raio de curvatura externo, enquanto o valor da largura é equivalente à largura da matriz:
Valores inseridos
Altura: (raio externo): 0,201 pol.
Largura (largura da matriz): 0,984 pol.
Valor Calculado
Comprimento do arco: 1,0845 pol.
Aqui, a profundidade da parábola (ou altura do arco) é de 0,201 pol. e o comprimento do arco da parábola é de 1,0845 pol. Lembre-se desses valores. Voltando agora à Calculadora de Arco Circular Completo em www.harsle.com, inserimos o comprimento do arco em 1,0845 pol. e a largura da matriz em 0,984 pol.
Valores inseridos
Comprimento do arco: 1,0845 pol.
Largura do arco (largura da matriz): 0,984 pol.
Valores Calculados
Altura do arco (raio de curvatura externo): 0,195 pol.
Ângulo Subtendido por Arco
(ângulo de curvatura incluído): 86,679 graus
Ao fazer isso, você verá que a altura do arco (ou seja, o raio externo) é de 0,195 pol., um pouco menor que o raio externo de 0,201 pol. da calculadora anterior, que não levou em consideração o efeito parábola. Sabendo disso, podemos afirmar com segurança que o raio interno diminui quando uma parábola é formada, o que ocorre ao usar um raio de punção menor que o raio mínimo de curvatura acentuada. Observe que a parábola também requer um ângulo de curvatura maior para produzir o ângulo de curvatura relaxado desejado; passamos de um ângulo de curvatura incluído de 89 para 86,68 graus, um retorno elástico adicional de 2,32 graus. Observe também que o raio interno da peça não ficará menor que o raio da ponta do punção.
- Ângulos e raios de curvatura
Lembre-se de que qualquer alteração no raio resulta em uma alteração no ângulo de curvatura. Se inserirmos a largura da matriz e o ângulo de curvatura incluídos em www.harsle.com, obteremos os resultados mostrados na Figura 2.
Os resultados mostram que, quando você modela o ar, o raio diminui com o ângulo de curvatura incluído (curvas acentuadas excluídas).
Essa relação ângulo/raio de curvatura para em ângulos incluídos menores que 28 graus incluídos (152 graus complementares), embora o ângulo mínimo incluído possa ser maior em materiais com retorno elástico significativo.
Isso se deve, em parte, ao fato de o ângulo mínimo de punção da prensa dobradeira ser de 28 graus, inclusive. Dito isso, continuar fechando a dobra além de 28 graus, inclusive, resultará em algum tipo de achatamento. O raio será esmagado até que o ângulo de dobra desejado seja alcançado ou uma operação de bainha seja concluída. (Uma observação rápida: para uma bainha fechada, o raio é zero e a dedução da dobra é calculada como uma porcentagem da espessura do material — 43% em condições ideais, embora seja uma operação muito dependente do operador.)
- Fatoração para resistência à tração
No exemplo anterior, usamos 1 grau de retorno elástico para fazer os cálculos. Para aço laminado a frio macio de 60 KSI, o retorno elástico médio é de 1 grau ou menos. E quanto aos outros materiais?
Para isso, podemos prever o retorno elástico com um grau razoável de precisão usando a fórmula a seguir, que exige a conversão de todos os valores para o sistema métrico. Observe que a previsão do retorno elástico nunca é 100% precisa. No entanto, essas fórmulas funcionam muito bem.
[(Raio interno em milímetros/2)/
Espessura do material em milímetros] × Fator de tração
Fator de tração = Resistência à tração do material em PSI/60.000
Primeiro, vamos calcular o retorno elástico como se estivéssemos trabalhando com nosso material de base de 60 KSI com um raio de curvatura interno de 0,170 pol.:
[(Raio interno em milímetros/2)/
Espessura do material em milímetros] × Fator de tração
Espessura do material: 0,125 pol. × 25,4 = 3,175 mm
Raio de curvatura interno: 0,170 pol. × 25,4 = 4,318 mm
(4.318/2) /3.175
2,159 mm / 3,175 mm = 0,68 graus de retorno elástico
Neste exemplo, arredondaremos para 1 grau. Podemos então aplicar o fator de tração para o aço inoxidável 88-KSI 304.
Fator de tração = Resistência à tração do material em PSI/60.000
88,000/60,000 = 1.466666
1,0 grau × 1,466666
Isso nos dá 1,46 graus para o aço inoxidável 88-KSI 304. Arredondando para cima, isso nos dá 1,5 grau de retorno elástico estimado com uma proporção de 1 para 1 entre o raio interno e a espessura do material.
- De volta à calculadora
Agora que você consegue estimar o retorno elástico com um nível razoável de precisão, pode compensá-lo. Para determinar o ângulo necessário para compensar o retorno elástico, basta subtrair o valor do retorno elástico se estiver trabalhando com ângulos de curvatura incluídos ou adicionar esse valor se estiver usando ângulos de curvatura complementares. A calculadora de arco circular em www.harsle.com funciona com ângulos de curvatura incluídos (novamente, denominados Ângulo de Arco Subtendido).
Depois de saber o raio interno — ou seja, o raio interno real que aparecerá na peça finalizada — você pode inserir esse valor de raio em suas fórmulas de dobra (veja a barra lateral).
Conclusão
Ao prever o raio interno corretamente, podemos calcular com precisão as deduções de curvatura. Das várias maneiras diferentes de prever o raio interno, nenhuma é perfeita, mas esta é a melhor possível. Ainda assim, a curvatura tem muitas variáveis para atingir 100% de precisão.
Também é fundamental na conformação a ar que o engenheiro ou programador informe o técnico sobre os conjuntos de ferramentas com os quais cada dobra foi projetada. Além disso, o técnico precisa compreender a importância absoluta do uso dessas ferramentas para obter peças de qualidade.
No próximo mês, abordaremos como calcular o raio interno de dobras onde a relação entre o raio interno e a espessura do material se torna muito grande — a dobra de raio profundo. Dobras de raio grande apresentam problemas com ângulo e largura da matriz, quebra múltipla e, claro, grandes quantidades de retorno elástico.
A toca do coelho ainda tem um longo caminho a percorrer, mas vale a pena a jornada.
Uma revisão das fórmulas de flexão
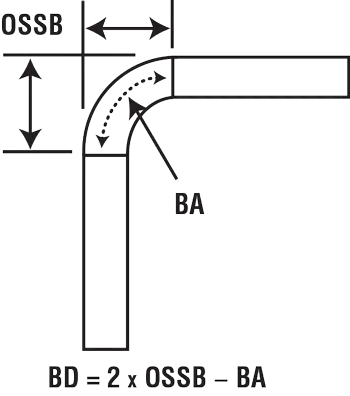
Essas fórmulas para tolerância de dobra, recuo externo e dedução de dobra são bem estabelecidas, e cada valor pode ser usado de diferentes maneiras para calcular o layout plano da peça.
Fórmulas
BA = [(0,017453 × Rp) + (0,0078 × Mt)]
× Graus de curvatura complementares
OSSB = [Tangente (grau de ângulo de curvatura/2)]
× (Mt + Rp)
BD = (OSSB × 2) – BA
Chave
Rp = Raio do nariz do punção (fundo)
ou o raio interno flutuado (formação de ar)
Mt = Espessura do material
BA = Tolerância de curvatura
BD = Dedução de curvatura
OSSB = Recuo externo
0,017453 = π/180
0,0078 = fator K × π /180
Fator K = 0,446










America-Miami-Customer-Feeback-1.jpg)
Uzbekistan-Customer-Feedback1.png)
Kosovo-Customer-Feedback11.png)
Russia-Customer-Feedback.jpg)
Russia-Customer-Feedback-3.jpg)






