Прогнозирование изгиба по внутреннему радиусу при использовании листогибочного пресса
По мере того, как я углубляюсь в тему прогнозирования Изгиб по внутреннему радиусу Используя листогибочный пресс, я обнаружил, что понимание тонкостей этого процесса может существенно повлиять на качество наших проектов по изготовлению металлоконструкций. Внутренний радиус играет решающую роль в обеспечении точности гибки и достижении желаемых результатов. В этой статье я поделюсь идеями и методами, которые помогли мне эффективно рассчитывать внутренний радиус при использовании листогибочного пресса, повышая эффективность и точность наших операций. Присоединяйтесь ко мне, чтобы изучить этот важнейший аспект металлообработки!
Предсказание радиуса никогда не бывает точным на 100 процентов, но это примерно то, что можно было бы сделать.
Вы можете использовать некоторые общие правила, чтобы предсказать внутренний радиус изгиба при воздушной формовке, и полученные вами результаты обычно достаточно близки, но с помощью нескольких онлайн-калькуляторов вы можете получить еще более точные результаты.
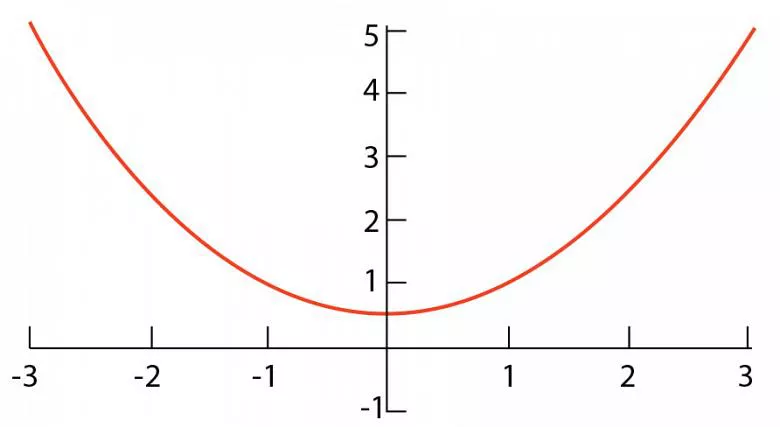
Зачастую в процессе формовки мы формируем не истинный радиус, а параболу.
Если вы следили за нашими обсуждениями в последние месяцы радиус изгиба И откуда он взялся, добро пожаловать обратно. В любом случае, посмотрим, насколько глубока эта кроличья нора.
В предыдущих статьях я обсуждал различные практические правила, которые операторы используют в цеху для выполнения работы. Эти правила могут приблизить ваш внутренний радиус гиба к истине, но можно добиться ещё большей точности.
Какая разница?
Рассмотрим типичную ситуацию, когда вы используете правило 20 процентов, которое гласит, что радиус изгиба на воздухе формируется как процент от отверстия матрицы: 20–22 процента для нержавеющей стали и около 16 процентов для холоднокатаной стали 60-KSI, нашего базового материала.
Допустим, вы гните мягкий алюминий твёрдостью 13 кДж (1300 кДж) с помощью матрицы шириной 0,984 дюйма (0,984 дюйма) и пуансона с радиусом 0,032 дюйма (0,032 дюйма). Для начала вы рассчитываете внутренний радиус изгиба на уровне 16% от раскрытия матрицы, который составляет 0,157 дюйма (0,157 дюйма), хотя это относится к материалу твёрдостью 60 кДж (600 кДж), поэтому вам нужно адаптировать его к типу материала. При этом, проверяя, получится ли острый изгиб, вы обнаруживаете, что минимальный радиус, при котором пуансон толщиной 0,032 дюйма (0,032 дюйма) начнёт сгибать линию изгиба, составляет 0,172 дюйма (0,172 дюйма). Наконец, вы проводите тестовый изгиб и обнаруживаете, что фактический радиус составляет 0,170 дюйма (0,170 дюйма).
У вас есть радиус 0,157 дюйма, рассчитанный по правилу 20 процентов, а затем радиус 0,172 дюйма, рассчитанный по вашим расчётам для острого изгиба. Это разница в радиусе 0,015 дюйма. Не так уж много, скажете вы? В этом случае разница, применённая к вычету изгиба, может достигать 0,009 дюйма на изгиб.
Вы когда-нибудь создавали деталь с четырьмя боковыми фланцами и четырьмя дополнительными фланцами сверху, а потом обнаруживали, что один угол получился идеальным, два угла — более-менее удовлетворительными, а один выглядит просто ужасно? Почему так происходит? Небольшая ошибка в расчёте изгиба, вызванная неточностями в расчётах внутреннего радиуса изгиба, может иметь большое значение, если вы хотите получить идеальные детали с первого раза.
Основой любой гибки является внутренний радиус изгиба. Если вы можете рассчитать вычет изгиба на основе фактических результатов, точность гарантирована. Единственный недостаток этой теории заключается в том, что во время формовки зачастую не формируется истинный радиус. Формируемая форма может представлять собой параболу – симметричную зеркально отраженную кривую, обычно U-образную, если ориентация показана на рисунке 1. А конечный радиус, который вы получаете, – это результат упругого возврата.
- Эффекты пружинения
Итак, как же нам спрогнозировать наиболее точный внутренний радиус гибки и правильное вычисление величины гиба? Чтобы сделать это вручную, математические вычисления становятся слишком сложными, поэтому я не буду в них углубляться. Вместо этого мы просто воспользуемся двумя разными веб-калькуляторами.
Первый вариант доступен на сайте www.harsle.com. Нажмите «Полный калькулятор дуги окружности». Обратите внимание, что ширина дуги в калькуляторе совпадает с шириной штампа, а угол, стягиваемый дугой, совпадает с углом изгиба.
Убедитесь, что настройки размеров калькулятора соответствуют используемым вами данным — дюймы, футы, миллиметры и т. д. Обратите внимание, что при нажатии Enter мы получаем чисто математические ответы, в которых не учитывается прочность материала на растяжение.
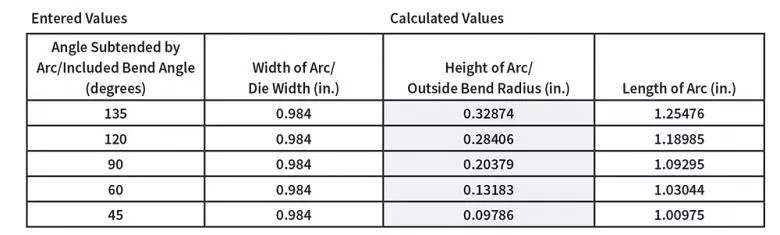
Как показано в этом расчете из The Complete Circular Arc Calculator на сайте www.harsle.com, по мере увеличения угла изгиба увеличивается и радиус (высота дуги).
Информация, которую мы ищем в калькуляторе, — это высота дуги, которая равна внешнему радиусу изгиба. Давайте найдём значение для нашего базового образца: холоднокатаной стали 60 кДж/дюйм, толщиной 0,125 дюйма (0,125 дюйма), используя ширину штампа 0,984 дюйма (0,984 дюйма). Обратите внимание, что мы обсуждаем воздушную формовку, поэтому угол штампа не имеет значения; это может быть швеллер, острый или V-образный штамп. Важна ширина.
Для начала давайте введем расслабленный угол — те 90 градусов, которых мы хотим достичь.
Введенные значения
Угол, образуемый дугой (включая угол изгиба): 90 градусов
Ширина дуги (ширина штампа): 0,984 дюйма.
Расчетное значение
Высота дуги (внешний радиус изгиба): 0,20379 дюйма.
Однако эти расчёты не учитывают упругое отклонение. В нашем примере мы используем значение упругого отклоненя в 1 градус, которое возникает при приблизительном соотношении толщины материала к внутреннему радиусу гиба 1:1. После того, как пуансон снимает давление формовки, материал отскакивает на 1 градус, поэтому для компенсации мы используем угол гиба 89 градусов включительно. Снова воспользуемся калькулятором Complete Circular Arc Calculator на сайте harsle.com и введём следующие данные:
Введенные значения
Ширина дуги (ширина штампа): 0,984 дюйма.
Угол, образуемый дугой (включая угол изгиба): 89 градусов
Расчетное значение
Высота дуги (внешний радиус изгиба): 0,201 дюйма.
Теперь берем значение высоты дуги для нашего нового угла изгиба и подставляем его в следующую формулу:
Высота дуги – (2 × Толщина материала2) = Внутренний радиус
0,201 – (2 × 0,01562) = Внутренний радиус изгиба
0,201 – 0,031 = 0,170 дюйма. Внутренний радиус изгиба
Обратите внимание, что этот подход с использованием высоты дуги отличается от подхода, использованного в рубрике «Основы гибки» за прошлый месяц, где мы использовали длину дуги. В прошлом месяце мы рассчитывали внутренний радиус на основе ширины отверстия штампа; на этот раз мы используем конкретный радиус.
В прошлом месяце мы рассчитали радиус 0,136 дюйма (0,136 дюйма), а только что рассчитали внутренний радиус другим методом и получили 0,170 дюйма (0,170 дюйма) — разница в 0,034 дюйма (0,034 дюйма). Кроме того, если бы мы использовали правило 20 процентов (опять же, для холоднокатаной стали 60 килофунтов на квадратный дюйм радиус рассчитывается примерно как 16 процентов от ширины штампа), мы бы рассчитали внутренний радиус 0,157 дюйма (0,157 дюйма) — это середина между двумя предыдущими измерениями. Все эти способы расчета радиуса немного различаются, и результаты немного различаются. Но да, кроличья нора становится глубже!
- Парабола и крутые повороты
Если вы используете значение радиуса пуансона, равное или меньше минимального радиуса острого изгиба для формовки детали воздухом, вы больше не будете создавать радиус в детали (более подробную информацию об острых изгибах см. здесь). Вместо этого вы будете создавать параболу. По сути, вы втягиваете в отверстие штампа дугу другой длины.
Чтобы предсказать, как будет формироваться эта парабола, мы можем обратиться к другому онлайн-калькулятору:
Вводим внешний радиус и ширину плашки, чтобы найти длину дуги параболы. Значение высоты в этом онлайн-калькуляторе эквивалентно внешнему радиусу изгиба, а значение ширины — ширине плашки:
Введенные значения
Высота: (внешний радиус): 0,201 дюйма.
Ширина (ширина штампа): 0,984 дюйма.
Расчетное значение
Длина дуги: 1,0845 дюйма.
Здесь глубина параболы (или высота дуги) составляет 0,201 дюйма (0,201 дюйма), а длина дуги параболы — 1,0845 дюйма (1,0845 дюйма). Запомните эти значения. Возвращаясь к калькулятору The Complete Circular Arc Calculator на сайте www.harsle.com, мы вводим длину дуги 1,0845 дюйма (1,0845 дюйма) и ширину штампа 0,984 дюйма (0,984 дюйма).
Введенные значения
Длина дуги: 1,0845 дюйма.
Ширина дуги (ширина штампа): 0,984 дюйма.
Расчетные значения
Высота дуги (внешний радиус изгиба): 0,195 дюйма.
Угол, опирающийся на дугу
(включая угол изгиба): 86,679 градусов
Когда вы это сделаете, вы увидите, что высота дуги (то есть внешний радиус) составляет 0,195 дюйма, что немного меньше внешнего радиуса 0,201 дюйма из предыдущего калькулятора, который не учитывал эффект параболы. Зная это, мы можем с уверенностью сказать, что внутренний радиус уменьшается при формировании параболы, что происходит при использовании радиуса пуансона, который меньше минимального радиуса острого изгиба. Обратите внимание, что парабола также требует большего угла изгиба для получения желаемого угла смягченного изгиба; мы перешли от включенного угла изгиба в 89 до 86,68 градусов, что составляет дополнительные 2,32 градуса упругого возврата. Также обратите внимание, что внутренний радиус детали не станет меньше радиуса вершины пуансона.
- Угол и радиусы изгиба
Помните, что любое изменение радиуса приводит к изменению угла гиба. Если ввести ширину штампа и угол гиба на сайте www.harsle.com, получим результаты, показанные на рисунке 2.
Результаты показывают, что при воздушном формовании радиус уменьшается с увеличением угла изгиба (исключая острые изгибы).
Соотношение угла изгиба и радиуса заканчивается при углах изгиба менее 28 градусов (152 градуса дополнительных), хотя минимальный угол изгиба может быть больше в материале со значительным упругим возвратом.
Отчасти это верно, поскольку минимальный угол изгиба пуансона гибочного пресса составляет 28 градусов включительно. При этом дальнейшее сгибание за пределы 28 градусов включительно приведёт к некоторому сплющиванию. Радиус будет сминаться до тех пор, пока не будет достигнут желаемый угол изгиба или не будет выполнена операция загибки. (Кстати, для закрытой кромки радиус равен нулю, а вычет загиба рассчитывается как процент от толщины материала — 43 процента в идеальных условиях, хотя это очень зависит от оператора.)
- Факторизация прочности на растяжение
В предыдущем примере мы использовали для расчётов 1 градус упругости. Для мягкой холоднокатаной стали с твёрдостью 60 кДж/дюйм средняя величина упругости составляет 1 градус или меньше. А как насчёт других материалов?
Для этого мы можем спрогнозировать упругость с приемлемой точностью, используя следующую формулу, которая требует перевода всех значений в метрическую систему. Обратите внимание, что прогнозирование упругости никогда не бывает стопроцентно точным. Тем не менее, эти формулы работают довольно хорошо.
[(Внутренний радиус в миллиметрах/2)/
Толщина материала в миллиметрах] × Коэффициент прочности на растяжение
Коэффициент прочности на растяжение = прочность материала на растяжение в фунтах на кв. дюйм/60 000
Сначала давайте рассчитаем упругое восстановление, как если бы мы работали с нашим базовым материалом плотностью 60 кДж с внутренним радиусом изгиба 0,170 дюйма:
[(Внутренний радиус в миллиметрах/2)/
Толщина материала в миллиметрах] × Коэффициент прочности на растяжение
Толщина материала: 0,125 дюйма × 25,4 = 3,175 мм
Внутренний радиус изгиба: 0,170 дюйма × 25,4 = 4,318 мм
(4.318/2) /3.175
2,159 мм/3,175 мм = 0,68 градуса упругости
В этом примере мы округлим это значение до 1 градуса. Затем можно применить коэффициент прочности на растяжение для нержавеющей стали марки 304 с прочностью 88 кДж/дюйм.
Коэффициент прочности на растяжение = прочность материала на растяжение в фунтах на кв. дюйм/60 000
88,000/60,000 = 1.466666
1,0 градус × 1,466666
Это даёт нам 1,46 градуса для нержавеющей стали марки 304 с индексом упругости 88-KSI. Округляя, получаем 1,5 градуса расчётного упругого возврата при соотношении внутреннего радиуса к толщине материала 1:1.
- Вернуться к калькулятору
Теперь, когда вы можете оценить упругость с достаточной точностью, вы можете её компенсировать. Чтобы определить угол, необходимый для компенсации упругости, просто вычтите значение упругости, если вы работаете с углами изгиба, входящими в состав дуги, или прибавьте его, если используете дополнительные углы изгиба. Калькулятор дуги окружности на сайте www.harsle.com работает с углами изгиба, входящими в состав дуги (также называемыми «стягиваемым углом дуги»).
Узнав внутренний радиус (то есть фактический внутренний радиус, который получится в готовой детали), вы можете вставить это значение радиуса в формулы гибки (см. боковую панель).
Заключение
Правильно предсказав внутренний радиус, мы можем точно рассчитать вычеты изгиба. Из множества способов предсказать внутренний радиус ни один не идеален, но этот — почти идеален. Тем не менее, гибка имеет слишком много переменных, чтобы достичь 100% точности.
При пневмоформовке инженер или программист также обязан сообщить техническому специалисту о наборах инструментов, с помощью которых был спроектирован тот или иной изгиб. Более того, технический специалист должен понимать абсолютную важность использования этих инструментов для получения качественных деталей.
В следующем месяце мы рассмотрим, как рассчитать внутренний радиус гибов, где соотношение между внутренним радиусом и толщиной материала очень велико — гибы с большим радиусом. Гибы с большим радиусом имеют проблемы с углом наклона матрицы, шириной матрицы, многократными поломками и, конечно же, очень сильным пружинением.
До кроличьей норы еще далеко, но путешествие того стоит.
Обзор формул изгиба
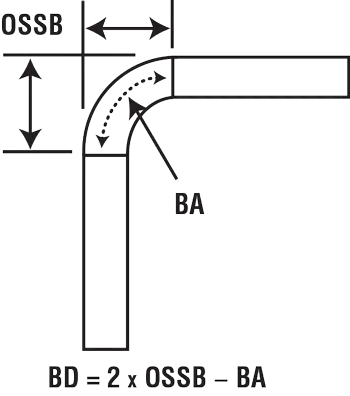
Эти формулы для допуска на изгиб, внешнего отступа и вычета изгиба хорошо известны, и каждое значение можно использовать по-разному для расчета компоновки плоской заготовки детали.
Формулы
БА = [(0,017453 × Rп) + (0,0078 × Мт)]
× Степени изгиба дополнительные
OSSB = [Касательная (градус угла изгиба/2)]
× (Мт + Рп)
БД = (ОССБ × 2) – БА
Ключ
Rp = Радиус носка пуансона (дна)
или плавающий внутренний радиус (формовка воздухом)
Mt = Толщина материала
BA = Допуск на изгиб
BD = вычет за изгиб
OSSB = Внешний отступ
0,017453 = π/180
0,0078 = K-фактор × π /180
Коэффициент К = 0,446










America-Miami-Customer-Feeback-1.jpg)
Uzbekistan-Customer-Feedback1.png)
Kosovo-Customer-Feedback11.png)
Russia-Customer-Feedback.jpg)
Russia-Customer-Feedback-3.jpg)






