Vorhersage der Biegung des Innenradius bei Verwendung einer Abkantpresse
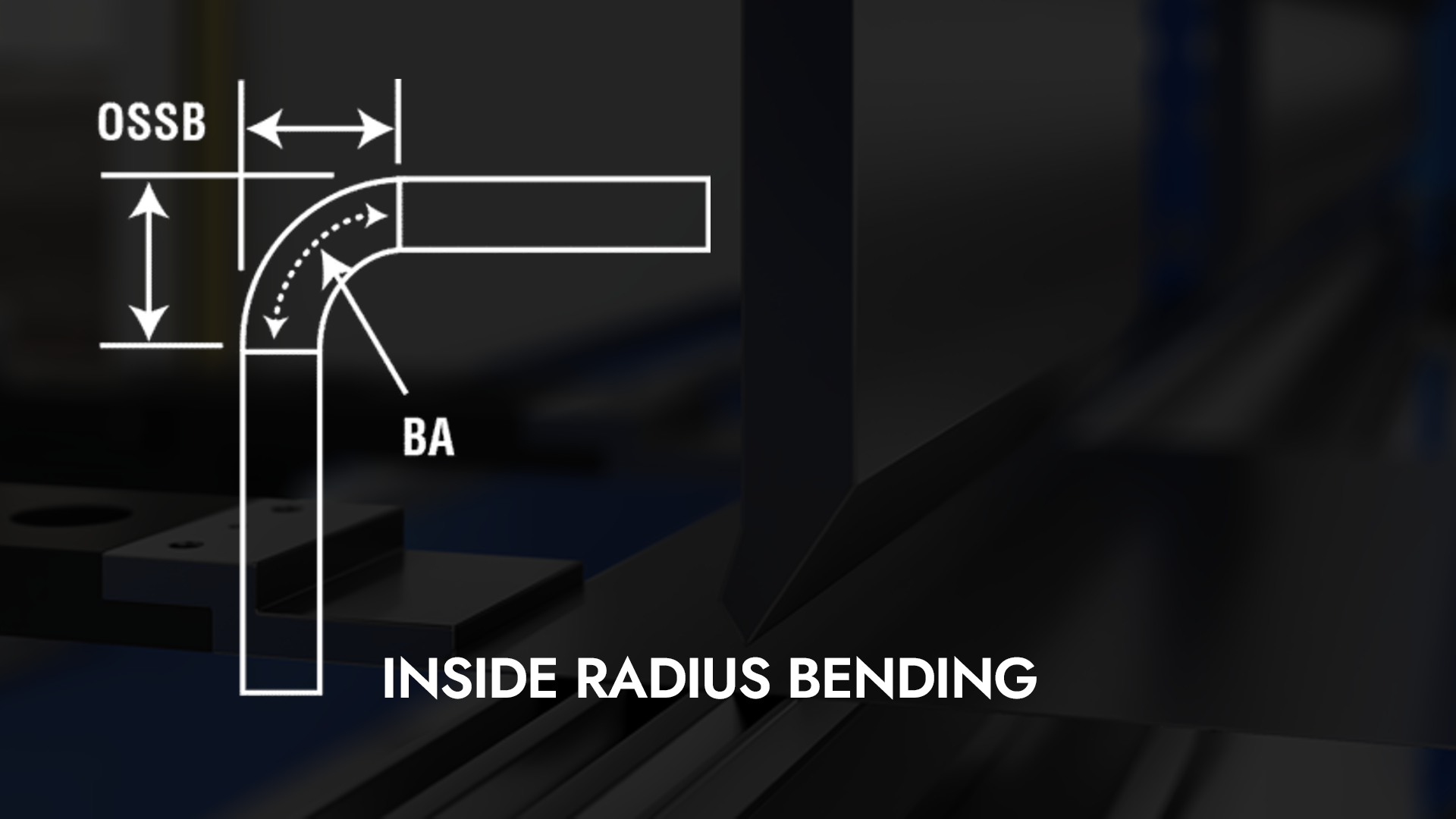
Wenn ich mich mit dem Thema Vorhersagen beschäftige Innenradiusbiegen Beim Einsatz von Abkantpressen habe ich festgestellt, dass das Verständnis der Feinheiten dieses Prozesses die Qualität unserer Metallbearbeitungsprojekte erheblich beeinflussen kann. Der Innenradius spielt eine entscheidende Rolle für präzise Biegungen und das Erreichen der gewünschten Ergebnisse. In diesem Artikel teile ich Erkenntnisse und Techniken, die mir geholfen haben, den Innenradius beim Einsatz einer Abkantpresse effektiv vorherzusagen und so sowohl die Effizienz als auch die Genauigkeit unserer Abläufe zu verbessern. Begleiten Sie mich bei der Erkundung dieses wesentlichen Aspekts der Metallbearbeitung!
Die Vorhersage des Radius ist nie hundertprozentig genau, aber so gut geht es nicht.
Sie können einige allgemeine Faustregeln verwenden, um die Biegung des inneren Biegeradius beim Luftformen vorherzusagen, und die Ergebnisse, die Sie erhalten, liegen normalerweise nahe genug beieinander, aber mit Hilfe einiger Online-Rechner können Sie noch näher herankommen.
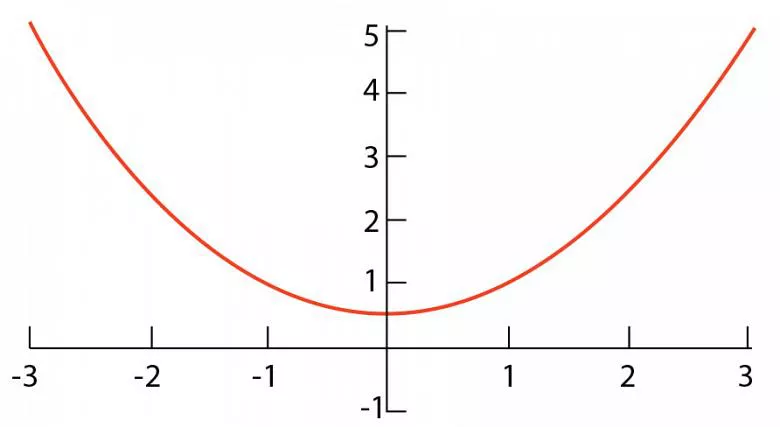
Beim Formen formen wir häufig keinen echten Radius, sondern eine Parabel.
Wenn Sie in den letzten Monaten unsere Diskussion über Biegeradius und woher es kommt, willkommen zurück. Wie dem auch sei, mal sehen, wie tief dieses Radius-Kaninchenloch geht.
In früheren Artikeln habe ich verschiedene Faustregeln besprochen, die Bediener in der Werkstatt anwenden, um ihre Arbeit zu erledigen. Mit diesen Regeln können Sie den inneren Biegeradius Ihrer Vorhersage sehr genau bestimmen, aber Sie können noch näher herankommen.
Welchen Unterschied macht es?
Stellen Sie sich eine typische Situation vor, in der Sie die 20-Prozent-Regel anwenden, die besagt, dass sich ein luftgebogener Radius als Prozentsatz der Matrizenöffnung bildet, 20 bis 22 Prozent für Edelstahl und etwa 16 Prozent für kaltgewalzten 60-KSI-Stahl, unser Basismaterial.
Angenommen, Sie biegen weiches 13-KSI-Aluminium mit einer Matrizenbreite von 0,984 Zoll und einem Stempel mit einem Radius von 0,032 Zoll. Als Ausgangspunkt berechnen Sie den inneren Biegeradius bei 16 Prozent der Matrizenöffnung mit 0,157 Zoll. Dies gilt allerdings für 60-KSI-Material, Sie müssen also den Wert an den Materialtyp anpassen. Wenn Sie gleichzeitig berechnen, ob die Biegung scharf wird, stellen Sie fest, dass der Mindestradius, bevor Ihr 0,032-Zoll-Stempel die Biegelinie zu knicken beginnt, 0,172 Zoll beträgt. Schließlich führen Sie eine Testbiegung durch und stellen fest, dass der tatsächliche Radius 0,170 Zoll beträgt.
Sie haben den Radius von 0,157 Zoll aus der 20-Prozent-Regel berechnet, dann haben Sie den Radius von 0,172 Zoll aus Ihren Berechnungen der scharfen Biegung. Das ist ein Radiusunterschied von 0,015 Zoll. Nicht viel, sagen Sie? In diesem Fall kann der Unterschied, wenn er auf den Biegungsabzug angewendet wird, 0,009 Zoll pro Biegung erreichen.
Haben Sie schon einmal ein Teil mit vier Seitenflanschen und vier zusätzlichen Flanschen an der Oberseite gebaut und dabei festgestellt, dass eine Ecke perfekt ist, zwei Ecken gerade noch zufriedenstellend sind und eine einfach nur schrecklich aussieht? Warum passiert das? Ein kleiner Fehler bei der Biegeableitung, der durch Abweichungen bei der Berechnung des inneren Biegeradius verursacht wird, macht einen großen Unterschied, wenn Sie gleich beim ersten Mal perfekte Teile haben möchten.
Der Kern jedes Biegevorgangs ist der Innenradius der Biegung. Wenn Sie den Biegeabzug anhand der tatsächlichen Ergebnisse berechnen können, ist Präzision gewährleistet. Der einzige Fehler dieser Theorie besteht darin, dass beim Formen oft kein echter Radius geformt wird. Die Form, die Sie formen, kann eine Parabel sein, eine symmetrische gespiegelte Kurve, die in der Regel U-förmig ist, wenn sie wie in Abbildung 1 dargestellt ausgerichtet ist. Der endgültige Radius ist das Ergebnis der Rückfederung.
- Rückfederungseffekte
Wie können wir also die genaueste Biegung des Innenradius und die korrekte Biegungsableitung vorhersagen? Die manuelle Berechnung ist mathematisch sehr aufwendig, daher werde ich hier nicht näher darauf eingehen. Stattdessen verwenden wir einfach zwei verschiedene webbasierte Rechner.
Den ersten finden Sie unter www.harsle.com. Klicken Sie auf den Kreisbogenrechner. Beachten Sie, dass die Bogenbreite im Rechner mit der Matrizenbreite übereinstimmt und der vom Bogen eingeschlossene Winkel mit dem eingeschlossenen Biegewinkel übereinstimmt.
Stellen Sie sicher, dass die Maßeinstellungen des Rechners für die von Ihnen verwendeten Daten (Zoll, Fuß, Millimeter usw.) richtig sind. Beachten Sie, dass die Antworten, die wir beim Klicken auf die Eingabetaste erhalten, rein mathematischer Natur sind und die Zugfestigkeit des Materials nicht berücksichtigt wurde.
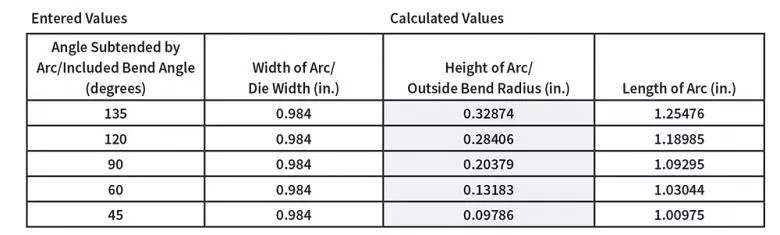
Wie diese Berechnung aus dem Complete Circular Arc Calculator unter www.harsle.com zeigt, nimmt mit zunehmendem Biegewinkel auch der Radius (die Höhe des Bogens) zu.
Die Information, die wir im Rechner suchen, ist die Bogenhöhe, die dem äußeren Biegeradius entspricht. Ermitteln wir einen Wert für unseren Basiswert, 60-KSI kaltgewalzten Stahl, 0,125 Zoll dick, mit einer Matrizenbreite von 0,984 Zoll. Bitte beachten Sie, dass wir über Luftumformung sprechen, daher spielt der Matrizenwinkel keine Rolle; es kann sich um eine Rillen-, Spitz- oder V-Matrize handeln. Entscheidend ist die Breite.
Lassen Sie uns zunächst den entspannten Winkel eingeben – die 90 Grad, die wir erreichen möchten.
Eingegebene Werte
Vom Bogen eingeschlossener Winkel (einschließlich Biegewinkel): 90 Grad
Bogenbreite (Matrizenbreite): 0,984 Zoll.
Berechneter Wert
Höhe des Bogens (äußerer Biegeradius): 0,20379 Zoll.
Diese Berechnungen berücksichtigen jedoch nicht die Rückfederung. Für unser Beispiel verwenden wir einen Wert von 1 Grad für die Rückfederung. Diese tritt auf, wenn das Verhältnis von Materialstärke zu innerem Biegeradius ungefähr 1:1 ist. Nachdem der Stempel den Umformdruck freigegeben hat, federt das Material um 1 Grad zurück. Zum Ausgleich verwenden wir nun einen Biegewinkel von 89 Grad inklusive. Wieder verwenden wir den Complete Circular Arc Calculator auf harsle.com und geben Folgendes ein:
Eingegebene Werte
Bogenbreite (Matrizenbreite): 0,984 Zoll.
Vom Bogen eingeschlossener Winkel (einschließlich Biegewinkel): 89 Grad
Berechneter Wert
Höhe des Bogens (äußerer Biegeradius): 0,201 Zoll.
Nun nehmen wir den Wert der Bogenhöhe für unseren neuen Biegewinkel und setzen ihn in die folgende Formel ein:
Höhe des Bogens – (2 × Materialstärke2) = Innenradius
0,201 – (2 × 0,01562) = Innerer Biegeradius
0,201 – 0,031 = 0,170 Zoll. Innerer Biegeradius
Beachten Sie, dass sich dieser Ansatz zur Bogenhöhe von dem Ansatz in der Kolumne „Biegegrundlagen“ des letzten Monats unterscheidet, als wir die Bogenlänge verwendeten. Letzten Monat berechneten wir einen Innenradius basierend auf der Breite der Matrizenöffnung; dieses Mal verwenden wir einen spezifischen Radius.
Letzten Monat haben wir einen Radius von 0,136 Zoll berechnet. Gerade haben wir den Innenradius mit einer anderen Methode berechnet und sind auf 0,170 Zoll gekommen – eine Differenz von 0,034 Zoll. Wenn wir außerdem die 20-Prozent-Regel anwenden (für kaltgewalzten 60-KSI-Stahl wird der Radius mit etwa 16 Prozent der Matrizenbreite berechnet), würden wir einen Innenradius von 0,157 Zoll berechnen – genau in der Mitte zwischen den beiden vorherigen Messungen. Dies sind alles verschiedene Möglichkeiten, einen Radius zu berechnen, mit leicht unterschiedlichen Ergebnissen. Aber ja, das Rätsel wird noch tiefer!
- Parabeln und scharfe Kurven
Wenn Sie einen Stempelradiuswert verwenden, der gleich oder kleiner als der minimale Biegeradius für die Luftformung eines Teils ist, erstellen Sie im Teil keinen Radius mehr (weitere Informationen zu Biegungen finden Sie hier). Stattdessen erstellen Sie eine Parabel. Tatsächlich ziehen Sie eine andere Bogenlänge in die Matrizenöffnung.
Um vorherzusagen, wie sich diese Parabel bilden wird, können wir auf einen anderen Online-Rechner zurückgreifen:
Wir geben unseren Außenradius und die Matrizenbreite ein, um die Bogenlänge der Parabel zu ermitteln. Der Höhenwert in diesem Online-Rechner entspricht dem äußeren Biegeradius, während der Breitenwert der Matrizenbreite entspricht:
Eingegebene Werte
Höhe: (Außenradius): 0,201 Zoll.
Breite (Matrizenbreite): 0,984 Zoll.
Berechneter Wert
Bogenlänge: 1,0845 Zoll.
Hier beträgt die Tiefe der Parabel (oder Höhe des Bogens) 0,201 Zoll und die Bogenlänge der Parabel 1,0845 Zoll. Merken Sie sich diese Werte. Kehren wir nun zum Rechner für komplette Kreisbögen unter www.harsle.com zurück und geben die Bogenlänge mit 1,0845 Zoll und die Matrizenbreite mit 0,984 Zoll ein.
Eingegebene Werte
Bogenlänge: 1,0845 Zoll.
Bogenbreite (Matrizenbreite): 0,984 Zoll.
Berechnete Werte
Höhe des Bogens (äußerer Biegeradius): 0,195 Zoll.
Winkel, der durch einen Bogen begrenzt wird
(einschließlich Biegewinkel): 86,679 Grad
Wenn Sie dies tun, werden Sie sehen, dass die Bogenhöhe (d. h. der Außenradius) 0,195 Zoll beträgt und damit etwas kleiner ist als der Außenradius von 0,201 Zoll aus dem vorherigen Rechner, der den Parabeleffekt nicht berücksichtigt hat. Mit diesem Wissen können wir davon ausgehen, dass der Innenradius abnimmt, wenn eine Parabel gebildet wird, was bei einem Stempelradius auftritt, der kleiner ist als der minimale Biegeradius. Beachten Sie, dass die Parabel auch einen größeren Biegewinkel erfordert, um den gewünschten entspannten Biegewinkel zu erzeugen; wir gingen von einem eingeschlossenen Biegewinkel von 89 auf 86,68 Grad, was einer zusätzlichen Rückfederung von 2,32 Grad entspricht. Beachten Sie auch, dass der Innenradius des Teils nicht kleiner wird als der Radius der Stempelnase.
- Winkel und Biegeradien
Bedenken Sie, dass jede Radiusänderung eine Änderung des Biegewinkels zur Folge hat. Wenn wir die Matrizenbreite und den eingeschlossenen Biegewinkel auf www.harsle.com eingeben, erhalten wir die in Abbildung 2 gezeigten Ergebnisse.
Die Ergebnisse zeigen, dass beim Luftformen der Radius mit dem eingeschlossenen Biegewinkel abnimmt (scharfe Biegungen ausgeschlossen).
Diese Biegewinkel-Radius-Beziehung endet bei eingeschlossenen Winkeln von weniger als 28 Grad (152 Grad komplementär), obwohl der minimale eingeschlossene Winkel bei Material mit erheblicher Rückfederung größer sein kann.
Dies liegt zum Teil daran, dass der minimale Stanzwinkel der Abkantpresse 28 Grad beträgt. Wird die Biegung jedoch über 28 Grad hinaus geschlossen, kommt es zu einer Abflachung. Der Radius wird so lange verkleinert, bis der gewünschte Biegewinkel erreicht oder ein Falzvorgang abgeschlossen ist. (Nebenbei bemerkt: Bei einem geschlossenen Saum ist der Radius null, und die Biegeabnahme wird als Prozentsatz der Materialstärke berechnet – unter idealen Bedingungen 43 Prozent, obwohl dies ein sehr bedienerabhängiger Vorgang ist.)
- Berücksichtigung der Zugfestigkeit
Im vorherigen Beispiel haben wir für die Berechnungen eine Rückfederung von 1 Grad verwendet. Bei 60-KSI-Weichstahl beträgt die durchschnittliche Rückfederung 1 Grad oder weniger. Wie sieht es mit anderen Materialien aus?
Mithilfe der folgenden Formel können wir die Rückfederung mit hinreichender Genauigkeit vorhersagen. Dazu müssen wir alle Werte in metrische Werte umrechnen. Bitte beachten Sie, dass die Vorhersage der Rückfederung nie hundertprozentig genau ist. Diese Formeln funktionieren jedoch recht gut.
[(Innenradius in Millimetern/2)/
Materialstärke in Millimetern] × Zugfaktor
Zugfaktor = Zugfestigkeit des Materials in PSI/60.000
Berechnen wir zunächst die Rückfederung, als würden wir mit unserem 60-KSI-Basismaterial mit einem inneren Biegeradius von 0,170 Zoll arbeiten:
[(Innenradius in Millimetern/2)/
Materialstärke in Millimetern] × Zugfaktor
Materialstärke: 0,125 Zoll × 25,4 = 3,175 mm
Innerer Biegeradius: 0,170 Zoll × 25,4 = 4,318 mm
(4.318/2) /3.175
2,159 mm /3,175 mm = 0,68 Grad Rückfederung
In diesem Beispiel runden wir dies auf 1 Grad auf. Anschließend können wir den Zugfaktor für 88-KSI 304-Edelstahl anwenden.
Zugfaktor = Zugfestigkeit des Materials in PSI/60.000
88,000/60,000 = 1.466666
1,0 Grad × 1,466666
Dies ergibt 1,46 Grad für 88-KSI 304 Edelstahl. Aufgerundet ergibt dies eine geschätzte Rückfederung von 1,5 Grad bei einem Verhältnis von 1:1 zwischen Innenradius und Materialstärke.
- Zurück zum Rechner
Da Sie die Rückfederung nun einigermaßen genau schätzen können, können Sie sie nun kompensieren. Um den Winkel zu bestimmen, den Sie zur Kompensation der Rückfederung benötigen, subtrahieren Sie einfach den Rückfederungswert, wenn Sie mit eingeschlossenen Biegewinkeln arbeiten, oder addieren Sie ihn, wenn Sie komplementäre Biegewinkel verwenden. Der Kreisbogenrechner auf www.harsle.com arbeitet mit eingeschlossenen Biegewinkeln (auch hier als „Unterer Bogenwinkel“ bezeichnet).
Sobald Sie den Innenradius kennen, also den tatsächlichen Innenradius, der im fertigen Stück erscheinen wird, können Sie diesen Radiuswert in Ihre Biegeformeln einfügen (siehe Seitenleiste).
Abschluss
Durch die korrekte Vorhersage des Innenradius können wir Biegeabzüge präzise berechnen. Von den verschiedenen Möglichkeiten zur Vorhersage des Innenradius ist keine perfekt, aber diese ist so gut wie möglich. Dennoch gibt es beim Biegen viel zu viele Variablen, um eine 100-prozentige Genauigkeit zu erreichen.
Beim Luftformen ist es außerdem unerlässlich, dass der Ingenieur oder Programmierer den Techniker über die Werkzeugsätze informiert, mit denen die jeweilige Biegung konstruiert wurde. Darüber hinaus muss der Techniker die absolute Bedeutung dieser Werkzeuge für die Herstellung hochwertiger Teile erkennen.
Nächsten Monat behandeln wir die Berechnung des Innenradius von Biegungen, bei denen das Verhältnis zwischen Innenradius und Materialstärke sehr groß wird – die Biegung mit großem Radius. Bei Biegungen mit großem Radius treten Probleme mit Matrizenwinkel, Matrizenbreite, Mehrfachbrüchen und natürlich sehr starker Rückfederung auf.
Es ist noch ein weiter Weg bis in den Kaninchenbau, aber die Reise lohnt sich.
Eine Überprüfung der Biegeformeln
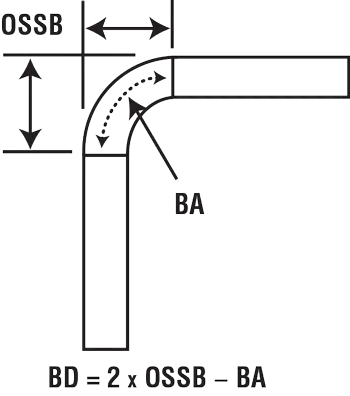
Diese Formeln für Biegezugabe, Außenrückschlag und Biegeabzug sind gut etabliert und jeder Wert kann auf unterschiedliche Weise verwendet werden, um das Flatblank-Layout des Teils zu berechnen.
Formeln
BA = [(0,017453 × Rp) + (0,0078 × Mt)]
× Grad der Biegung komplementär
OSSB = [Tangente (Grad des Biegewinkels/2)]
× (Mt + Rp)
BD = (OSSB × 2) – BA
Schlüssel
Rp = Radius der Stempelnase (Boden)
oder der schwebende Innenradius (Airforming)
Mt = Materialstärke
BA = Biegezugabe
BD = Biegeabzug
OSSB = Außenrückschlag
0,017453 = π/180
0,0078 = K-Faktor × π /180
K-Faktor = 0,446










America-Miami-Customer-Feeback-1.jpg)
Uzbekistan-Customer-Feedback1.png)
Kosovo-Customer-Feedback11.png)
Russia-Customer-Feedback.jpg)
Russia-Customer-Feedback-3.jpg)






